干扰对齐作为一种新颖的干扰处理方法, 近年来得到了学术界广泛的关注^[1].在实现干扰对齐时，一般采用有限反馈的技术来获取信道状态信息(CSI，channel state information)^[2].以前基于有限反馈干扰对齐的性能分析都是基于单个的小区性能分析，或者基站部署是基于规则的Wyner模型、正六边形格模型，但在实际的网络部署中，很多基站或者节点位置以及家庭基站的部署位置都是随机的.最近引入随机的模型可以准确地研究实际无线通信系统的中断概率和网络容量性能^[3]，并且能得到闭合的信干扰比和成功覆盖率以及网络容量的闭合表达式，定量地分析网络的性能，而基于规则的格模型的性能分析只能依靠蒙特卡洛仿真得到.笔者在泊松域上研究基于有限反馈的干扰对齐技术.

在多输入多输出(MIMO, multiple input multiple output)干扰网络中，假设发射机在平面上服从一个密度为λ的齐次泊松过程^[3](PPP，Poisson point process).每个发射机有N_t根发射天线，和它的目的单用户进行通信，用户的天线数为N_r.假设发射机k发送信号给它的目的用户k，它可能对网络中其他的用户造成干扰.在K个用户的干扰网络中使用H_{k, i}表示发射机i和用户k之间的信道，p表示发射机的功率，n表示路径衰落指数，r_{k, i}表示发射机i和用户k之间的距离，d_i表示发射机发送d_i个独立的数据流给用户，H_{k, i}∈C^N_r×N_t表示块衰落信道，服从零均值单位方差的复高斯分布.那么，在用户k上接收信号的表达式为

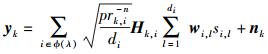
(1)

其中：y_k为N_r维信号矢量，ϕ(λ)为泊松过程，s_{i, l}表示来自发射机i的第l个数据流，w_{i, l}为相应的预编码矢量，n_k为零均值方差为σ²I_Nr的加性高斯白噪声.用户k使用接收矢量v_{k, j}来检测第j流数据：

(2)

式(2) 中右边第1项表示期望的信号，第2项表示数据流之间的干扰，第3项表示发射机之间的干扰. T₀表示发送目标数据给用户k的接收机，ϕ(λ)\T₀表示在泊松域ϕ(λ)里除了T₀以外的其他发射机的集合.假设K个用户组成一个协作的簇，为了消除干扰，对在这个协作的簇里面的信道链接利用干扰对齐技术来设计预编码矢量和接收机矢量^[1]：

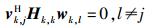
(3)

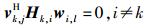
(4)

在有限反馈设计时，信道信息矩阵H_{k, i}被矢量化，h_{k, i}=vec(H_{k, i})，接收机k从随机矢量量化(RVQ，random vector quantization)码本^[4] 中依据以下准则选取最优的码字：

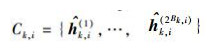
(5)

其中：表示信道方向信息，码本中码字的个数为2^{B_{k, i}}，B_{k, i}为反馈的比特数目.本研究中假设反馈信道是零延时理想的信道.

首先计算检测信号的信干扰比，然后利用RVQ技术对信道信息进行量化，接着对量化信道的相关统计特征进行分析.

发射端获取了有限反馈的信息状态信息，这样就造成了干扰的泄漏，那么用户k接收到的第j流数据的信干扰比为

(6)

其中：，符号⊗表示Kronecker积；I_{k, j}为总的干扰.

(7)

其中T_{j, l}^{(k, i)}=w_{k, l}⊗v_{k, j}^H.

利用RVQ码本对信道状态信息量化为

(8)

其中：表示信道方向信息的量化误差，为量化后的信道方向信息，s_{k, i}为分布在零空间上的单位矢量.干扰对齐的预编码矢量和接收矢量的设计都是基于量化的信道方向信息.

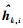
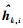
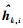
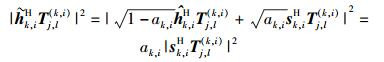
(9)

式(9) 中用到了干扰对齐的式(3) 和式(4).那么，总的干扰可以表示为

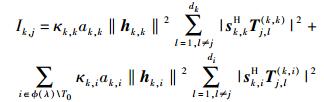
(10)

为了计算的方便，令

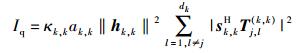
(11)

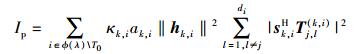
(12)

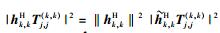
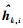
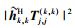
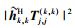
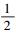
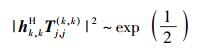
首先分析期望信号部分的信道相关统计特征，，T_{j, j}^{(k, k)}是由h_{k, i}的量化信道, (i≠k)决定的，它独立于h_{k, k}^[2]，‖h_{k, k}^H‖²服从卡方分布服从参数为1和N_tN_r－2的Beta分布，即~Beta(1, N_tN_r－2).那么2个变量的积|h_{k, k}^HT_{j, j}^{(k, k)}|²服从自由度为2的卡方分布：|h_{k, k}^HT_{j, j}^{(k, k)}|²~χ²(2)，也是服从指数为的指数分布：

(13)

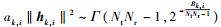
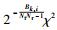
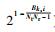
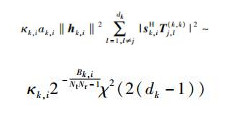
接着分析干扰信号部分的信道相关统计特征，a_{k, i}‖h_{k, i}‖²服从Gamma分布，表示为^[2]；|s_{k, i}^HT_{j, l}^{(k, k)}|²服从参数为1和N_tN_r－2的Beta分布，表示为|s_{k, i}^HT_{j, l}^{(k, k)}|²~Beta(1, N_tN_r－2).那么2个变量的积服从卡方分布，可以表示为a_{k, i}‖h_{k, i}‖²|s_{k, i}^HT_{j, l}^{(k, k)}|²~ (2)，卡方分布可以写成Gamma分布的形式，也就是a_{k, i}‖h_{k, i}‖²|s_{k, i}^HT_{j, l}^{(k, k)}|²~Γ(1, )，那么可以得到

写成Gamma分布形式为

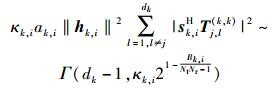
(14)

那么

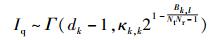
(15)

中断概率是评估通信系统的一项非常重要的性能指标，它定义为信干扰比小于某个目标阈值的概率P{γ_{k, j}≤β_{k, j}}=1-P{γ_{k, j}≥β_{k, j}}，P{γ_{k, j}≥β_{k, j}}表示成功覆盖率.下面计算系统的中断概率.

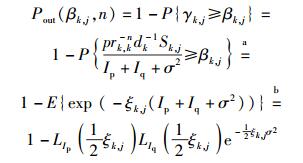
(16)

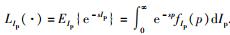
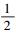
其中：ξ_{k, j}=β_{k, j}r_{k, k}ⁿp^-1d_k，β_{k, j}为信噪比的阈值；S_{k, j}=|h_{k, k}^HT_{j, j}^{(k, k)}|²；L_Ip(·)表示变量I_p的拉普拉斯变换，公式(16) 中步骤a用到了式(13) 中S_{k, j}服从指数分布：S_{k, j}~exp()，步骤b用到了拉普拉斯变换的定义.

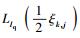
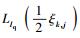
中断概率的计算转化为计算、.下面首先来计算，在式(15) 中得到.假设一随机变量X服从Gamma分布：X~Γ(k₁, θ₁)，则X的拉普拉斯变换为L_X(s)=(1+sθ₁)^-k₁.于是得到

(17)

接下来计算：

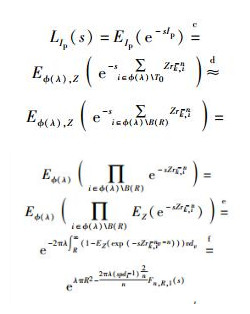
(18)

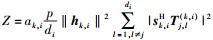
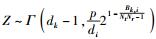
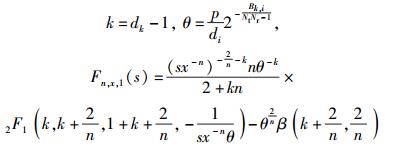
其中步骤c中，，由式(12) 可得.在步骤d中，B(R)为一个保护区域，也就是假设发射机的位置为圆心，用户所在的半径R的圆里面只有一个发射机.步骤e用到泊松过程的概率生成函数^[3].在步骤f中计算了变量Z~Γ(k, θ)函数的期望，其中：

其中：₂F(·)为高斯超几何函数，β(·)为贝塔欧拉函数^[5].

由式(17)、式(18) 计算中断概率：

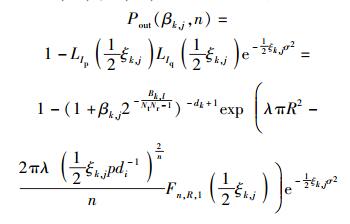
(19)

网络容量是指区域的频谱效率，定义为成功覆盖率和在单位面积上的最大和速率的乘积^[6].当数据流在网络中发送时，它的网络容量为

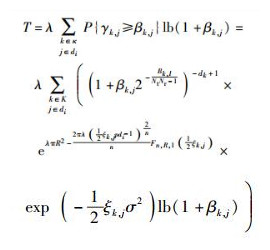
(20)

首先求出网络容量的下界T_down，然后为了使得网络容量最大化，求出最优的发射机部署密度，也就是最优的泊松过程密度λ^opt.

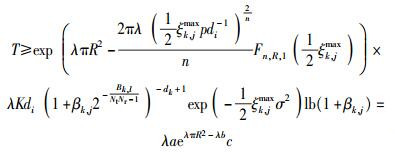
(21)

T_down的计算利用了用户均匀分布在半径为R的圆内这个假设，也就是说发射机距离自己的用户最远距离为R.其中：

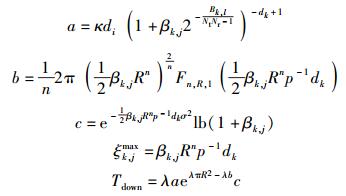
利用T_down对λ求导数可以得到最优的发射机部署密度λ^opt.

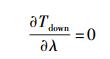
(22)

求解式(22) 得到

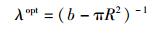
(23)

仿真参数设置：路径衰减系数n为4，半径R设为2 m，每个发射机发射的数据流个数都是2.

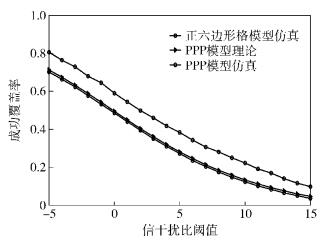
图 1蒙特卡洛仿真比较了MIMO干扰网络基于规则的和不规则的基站部署模型下利用干扰对齐技术进行预编码和解码设计系统的成功覆盖率性能.仿真次数为10 000次，收发天线数目都为4，用户数为3，在发射端基于有限反馈获取CSI，反馈比特数为12 bit.规则的基站部署采用的是传统的正六边形格模型，设正六边形的边长为R_grid，那么基站的部署密度为面积的倒数即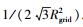.不规则的基站部署采用PPP模型，PPP的基站部署密度和六边形格的部署密度同为0.01，由密度可以求出R_grid.从仿真图中可以看出，基于格模型的成功覆盖率模型的性能要高于基于泊松过程的性能.这是因为泊松过程的基站是独立随机放置的，而正六边形格模型基站位置之间具有很强的相关性^[3].

图 1

图 1

图 1 不同模型下系统的成功覆盖率

在MIMO干扰网络中，收发天线数目都为4，用户数为3，在发射端基于有限反馈获取CSI，系统的中断概率随泊松过程密度变化的关系如图 2所示.有限反馈的比特数目分别为6、8、10、12 bit，信干扰比阈值为3 dB.从图 2中可以看出，反馈比特数目的增加会提高系统的性能.

图 2

图 2

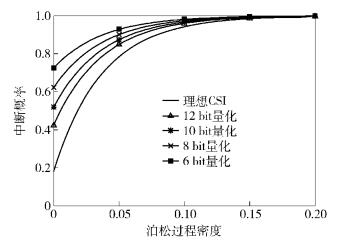
图 2 系统的中断概率随泊松过程密度变化

网络容量在理想CSI下和不同反馈比特数下的随密度变化的曲线如图 3所示.设置信噪比为15 dB，信干扰比阈值为3 dB，用户数为3.从图 3中可以看出，理论和蒙特卡洛仿真实验的结果非常吻合.随着反馈比特数的增加，系统的网络容量随之增加.在有限反馈比特数一定的情况下，系统的网络容量是发射机服从泊松分布的密度函数，函数存在一个极值点，容量不会随着密度的增加无限地增加.这是因为开始的网络容量的增加是来自自由度的增益，但是随着密度的增加，多发射机之间的干扰使得系统快速变成了一个干扰受限的系统，系统的信干扰比减小了，从而网络容量减小了.于是存在一个最佳的发射机密度.

图 3

图 3

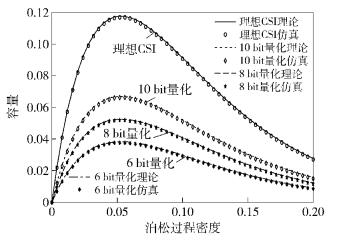
图 3 网络容量随泊松过程密度变化

笔者在泊松域上分析了基于有限反馈的干扰对齐系统性能，这对实际网络中小区的规划、基站的部署奠定了理论基础.