2. 中国工程物理研究院 院机关, 四川 绵阳 621999
为提高复合线性调频(CLFM)信号的距离速度联合分辨力, 提出了一种基于分数阶傅里叶变换的旋转线性调频(RLFM)信号, 给出了设计方法, 仿真得到了RLFM信号的模糊函数图、-3 dB模糊度图、距离模糊函数图及速度模糊函数图, 最后将其与CLFM信号进行了对比, 结果显示, 当旋转角度α满足1/2 < cos α < 5/6时, RLFM信号具有更好的速度分辨力和距离速度联合分辨力.
2. Administrative agency, China Academy of Engineering Physics, Mianyang 621999, China
In order to improve the joint distance-velocity-resolution of the composed linear frequency modulation (CLFM) signal, a rotated linear frequency modulation (RLFM) signal based on fractional Fourier transform is proposed. The design method of RLFM signal is given, and the simulations of the signal about the ambiguity function, -3 dB ambiguity graph, distance ambiguity graph and velocity ambiguity graph have been presented. Finally to put RLFM signal and CLFM signal are compared. The differences of them show that the RLFM signal has a better performance on velocity resolution and joint distance-velocity-resolution than the CLFM signal.
现代雷达为了解决探测距离和速度分辨力之间的矛盾[1],常采用调频或调相的方法来增加信号带宽,线性调频(LFM, linear frequency modulation)信号中的CLFM信号由于具有比单斜率LFM信号更好的速度分辨力和距离速度联合分辨力而备受青睐[2].然而,由于CLFM信号的调频斜率是一对互为相反数,随着现代雷达截获技术日趋成熟,常规的LFM类信号比较容易被截获,因此,正在研究复杂类型的LFM类信号.本研究根据分数阶傅里叶变换(FRFT, fractional Fourier transform)的时频旋转特性,设计了一种RLFM信号.该信号具有不同的调频斜率,因此不存在距离速度耦合[3],且在旋转角度α未知的情况下,具有更好的低截获性能[4].通过RLFM信号模糊函数[5]仿真分析得知,其距离速度联合分辨力相对CLFM信号得到提高.
1 FRFT
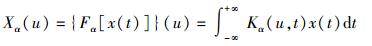
|
(1) |
其中下标表示角度为α的连续FRFT,其变换核为
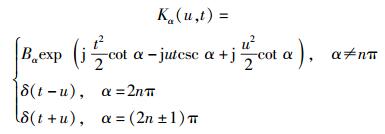
|
(2) |
其中: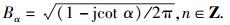
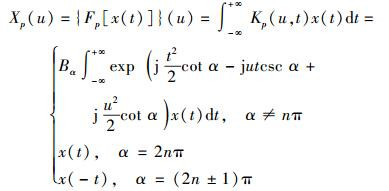
|
(3) |
式(3) 给出的FRFT定义是线性的,但它不是移不变的.其中α=p×π/2,当p=1时,X1(u)是x(t)的普通傅里叶变换;当p=-1时,X-1(u)是x(t)的普通傅里叶逆变换[8-9].分析式(3) 得知,以p(或α)为参数的FRFT定义是以4(或2π)为周期的函数,因此只需要考查区间p∈(-2, 2](或α∈(-π, π])即可.根据定义式(3),函数的0阶变换就等于该函数本身.
2 RLFM信号的分析与设计RLFM信号是在正负双斜率的基础上,多增加了1个周期、时间频率函数在时频平面逆时针旋转一定角度α得到的.下面将给出双周期CLFM信号及RLFM信号具体的时间频率函数关系及图形.
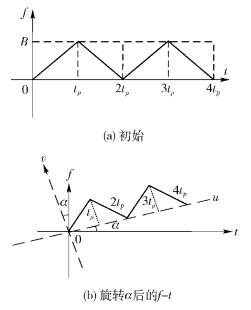
图 1所示为RLFM信号的频率时间函数和双周期CLFM信号的频率时间函数的关系.首先写出双周期CLFM信号的频率时间函数关系,然后根据旋转矩阵得到在时频面旋转角度α后的RLFM信号的频率时间函数关系式.
|
图 1 RLFM信号的频率时间函数关系 |
双斜率CLFM信号的频率时间函数关系可表示为
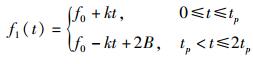
|
(4) |
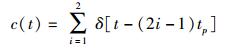
|
(5) |
其中:f0为中心频率,|k|=B/tp.则双周期CLFM信号的频率时间函数关系可表示为
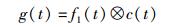
|
(6) |
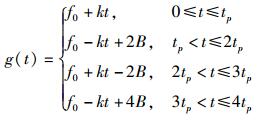
|
(7) |
又时间-频率平面上的二维旋转变换矩阵为
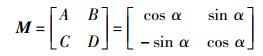
|
(8) |
利用旋转矩阵,可推导出绕原点旋转α后的频率时间函数关系式,具体推导过程如下.
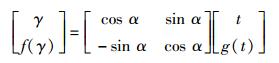
|
(9) |
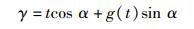
|
(10) |
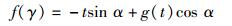
|
(11) |
令k1=tan (α+arctan k),k2=tan (π+α-arctan k),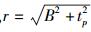
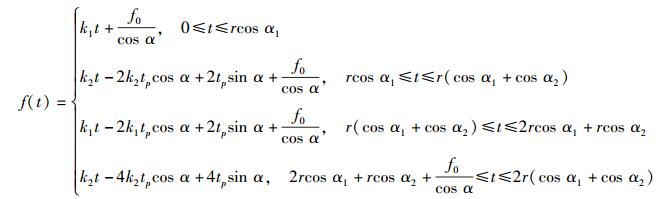
|
(12) |
则幅度为A的RLFM信号复包络的表达式为
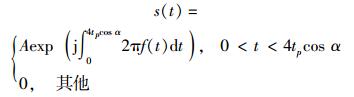
|
(13) |
由于RLFM信号的表达式复杂,其模糊函数的理论推导过程也相当繁琐,下面将通过其模糊函数仿真来分析RLFM信号的分辨力情况.
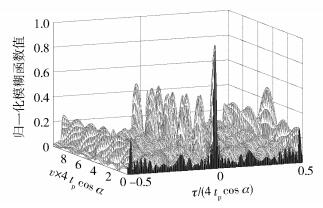
将时宽带宽积为40的正负双斜率LFM信号的频率时间函数拓展一个周期,然后逆时针旋转π/5. 图 2为采用Matlab仿真绘制α=π/5的RLFM信号的模糊函数图,由图 2可知,RLFM信号的模糊函数图呈近似图钉状,两直线在原点处叠加,主瓣孤立而凸起,在0.5倍时宽处有两直线叠加,但形成的峰值远小于主峰.
|
图 2 RLFM信号的模糊函数 |
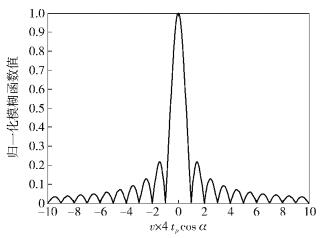
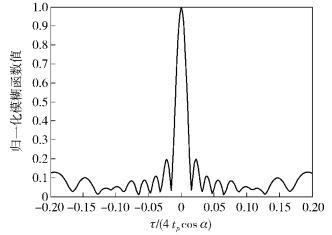
图 3为RLFM信号的速度模糊函数图,图中显示RLFM信号的速度模糊函数是辛格函数,速度瑞利分辨力为1/(4tpcos α). 图 4为RLFM信号的距离模糊函数图,图中显示RLFM信号的距离瑞利分辨力约为0.015×4tpcos α,即0.06tpcos α.而CLFM信号和单斜率LFM信号的距离瑞利分辨力约为0.05tp[10].因此,当cos α < 5/6时,RLFM的距离瑞利分辨力比CLFM的距离瑞利分辨力好.本次仿真旋转角α=π/5,其距离瑞利分辨力为0.015×4tpcos (π/5)≈0.485tp,比正负对称双斜率CLFM的距离瑞利分辨力好.
|
图 3 RLFM信号的速度模糊函数 |
|
图 4 RLFM信号的距离模糊函数 |
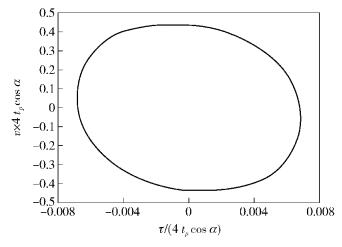
图 5为RLFM信号的-3 dB模糊度图.图中显示RLFM信号的距离分辨力约为0.013×4tpcosα=0.042tpcosα,速度分辨力约为0.9/(4tpcosα)=0.225/(tpcosα).
|
图 5 RLFM的-3 dB模糊度 |
而CLFM信号的距离分辨力约为0.022×2tp=0.044tp,速度分辨力约为0.9/(2tp)=0.45/tp[10].由于cosα≤1,所以RLFM信号的距离分辨力优于正负对称双斜率CLFM信号.当cosα > 1/2时,RLFM信号的速度分辨力优于正负对称双斜率的CLFM信号.并且图 5显示,RLFM信号的-3 dB模糊度图的形状与CLFM信号差不多,面积大约是CLFM信号-3 dB模糊度图面积的2/3,因此,RLFM信号相对CLFM信号的距离速度联合分辨力有提高.
4 结束语由FRFT的时频旋转特性,设计了一种RLFM信号.该信号具有不同的调频斜率,因此不存在距离速度耦合.采用Matlab仿真绘制α=π/5的RLFM信号的模糊函数图、距离模糊函数图、速度模糊函数图及-3 dB模糊度图.通过分析得知,当旋转角度α满足1/2 < cos α < 5/6时,RLFM信号比正负双斜率CLFM信号及单斜率LFM信号具有更好的距离分辨力、速度分辨力和距离速度联合分辨力.
| [1] | Klauder J R, Price A C, Darlinton S, et al. The theory and design of chirp radars[J].The Bell System Technical Journal, 1960, 39(4): 745–809. doi: 10.1002/bltj.1960.39.issue-4 |
| [2] | Besson O, GhoGho N, Swami A. Parameter estimation for random amplitude chirp signals[J].IEEE Transac-tions on signal processing, 1999, 47(12): 3208–3219. doi: 10.1109/78.806067 |
| [3] | 凌太冰. LFMCW雷达运动目标检测与距离速度去耦合[D]. 成都: 电子科技大学, 2003: 4-9, 43-50. |
| [4] |
张小乾, 王凌, 姚远程, 等. 基于FRFT与WVD的旋转LFM信号参数估计[J]. 通信技术, 2012, 45(12): 33–36.
Zhang Xiaoqian, Wang Ling, Yao Yuancheng, et al. Rotated LFM signal parameter estimation based on FRFT and WVD[J].Communications Technology, 2012, 45(12): 33–36. doi: 10.3969/j.issn.1002-5561.2012.12.011 |
| [5] | Dele G W. Wave form design, in radar handbook[M]. 1th ed. New York: McGraw-Hill, 1970: 3-7. |
| [6] | Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J].IEEE Transactions on Signal Processing, 2000, 44(9): 2141–2150. |
| [7] |
陈小龙, 王国庆, 关键, 等. 基于FRFT的动目标检测模型与参数估计精度分析[J]. 现代雷达, 2011, 33(5): 39–45.
Chen Xiaolong, Wang Guoqing, Guan Jian, et al. Analysis of model of moving target detection and precision of parameter estimation based on FRFT[J].Modern Radar, 2011, 33(5): 39–45. |
| [8] | Tao Ran, Li Bingzhao, Wang Yue. New sampling formulae related to linear canonical transform[J].Signal Processing, 2007, 87: 983–990. doi: 10.1016/j.sigpro.2006.09.008 |
| [9] | Zayed A I. A convolution and product theorem for the fractional fourier transform[J].IEEE Signal Processing Letters, 2010, 5: 101–103. |
| [10] |
刘领容, 王凌, 姚远程, 等. 复合线性调频信号的模糊函数分析[J]. 西安理工大学学报, 2011, 27(4): 481–485.
Liu Lingrong, Wang Ling, Yao Yuancheng, et al. Analysis of ambiguity function of combined linear frequency modulation signal[J].Journal of Xi'an University of Technology, 2011, 27(4): 481–485. |


