2. 重庆大学 飞行器测控与通信教育部重点实验室, 重庆 400044
提出了一种针对过时信道状态下机会双向中继系统的第N最优中继选择算法.分析了该算法在过时信道状态下的中断率性能, 即通过中继选择时刻信噪比的概率密度函数和以它为条件的数据传输时刻信噪比的条件概率密度函数, 确定数据传输时刻信噪比的概率密度函数, 给出系统中断率下界的闭式表达及其在高信噪比下的近似值.仿真结果表明, 新算法的中断率理论结果同蒙特卡罗仿真结果相重合, 且在高信噪比下, 其近似表达结果能很好地逼近理论结果.
2. Key Laboratory of Aerocraft Tracking Telemetering and Command and Communication, Ministry of Education, Chongqing University, Chongqing 400044, China
Under the outdated channel state information, a scheme of the N-th best relay selection was proposed for the N-th best relay adoption in opportunistic two-way relay cooperative networks. The outage performance was discussed. The closed-form lower bound of the outage probability and its asymptotic expression for the high signal-to-noise ratio (SNR) regime were given based on the probability density function (PDF) of the SNR for the data transmission instant, which is obtained from the PDF of the SNR for the relay selection instant and the conditional PDF of the SNR for the data transmission instant. Simulations show that the analyses are close to the simulated ones, and the asymptotic results very well match the simulated ones in the high SNR regime.
传统的协同通信系统通常以半双工的方式传输数据[1-3].为提高频谱利用率,双向中继协同通信受到广泛的关注[4-7],Hwang等[8]首次对过时信道状态下的机会双向中继选择进行了研究.在实际环境中,由于网络调度、负载平衡等原因,第1最优中继可能已经承担了其他任务,无法作为当前任务的中继节点,因此需要选择第N最优中继.从性能评估的角度看,若系统网络选择了错误的最优中继,第N最优中继选择算法将有利于评估在最优中继选择有误的情况下,系统性能的恶化程度.特别地,最优中继选择算法是第N最优中继选择算法在N=1时的一个特例.综上,本研究以过时信道信息下的机会双向中继协同通信系统为研究对象,提出了一种第N最优中继选择算法,研究了中断率性能,给出中断率下界的闭式表达及其在高信噪比下的近似值.
1 系统模型笔者所研究的机会双向中继系统包含2个源节点A和B,M个中继节点,记为Rm,m=0, 1, …, M-1.假设源节点A和B之间需要相互发送数据,并从M个中继节点中选择1个中继节点,用于数据的转发.假设A和B之间没有直接传输路径.
源节点A和B之间的数据交换需要2个时隙.第1个时隙,A和B分别发送信号xA和xB到M个中继节点,于是任意1个中继点Rm收到的信号可以表示为
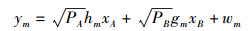
|
(1) |
其中:PA和PB分别表示节点A和B的数据发射功率;hm表示A和Rm间的信道,gm表示B和Rm间的信道,这里采用的信道模型为复高斯信道,记为hm~CN(0, d-αA, Rm),gm~CN(0, d-αRm, B),α是路径损耗因子,dA, Rm和dRm, B分别表示节点A和Rm,以及节点B和Rm的归一化距离,wm表示均值为零,方差为N0的加性复高斯白噪声,即wm~CN(0, N0).
假设信道满足互易性,且节点A和B已将自干扰消除,于是在第2个时隙,节点A和B所接收到的信号分别记为
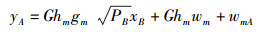
|
(2) |
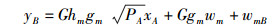
|
(3) |
其中:Rm的放大系数为
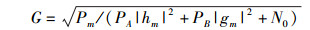
|
Pm表示Rm的发射功率,wmA~CN(0, N0)和wmB~CN(0, N0)表示均值为零、方差为N0的加性复高斯白噪声.取各节点的发射功率相同,即PA=PB=Pm=P,则A→Rm→B和B→Rm→A的端到端信噪比分别可写为
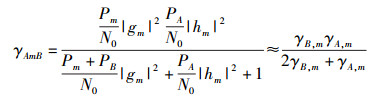
|
(4) |
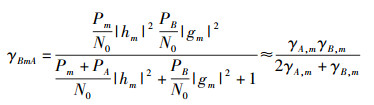
|
(5) |
其中:γA, m=(P/N0)|hm|2表示A和Rm之间信道的信噪比,γB, m=(P/N0)|gm|2表示B和Rm之间信道的信噪比,其均值分别记为γA, m=(P/N0)d-αA, Rm和γB, m=(P/N0)d-αRm, B.
2 机会双向中继选择算法本研究考虑信道是缓慢时变的,在中继选择时刻,采用的信道状态是hm和gm,而在数据传输时刻,信道状态发生了变换,记为ĥm和ĝm,分别对应hm和gm的过时信道状态.将前后两个信道之间的关系表示为[9]
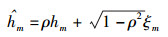
|
(6) |
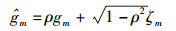
|
(7) |
其中:ξm和ζm服从复高斯分布,记为ξm~CN(0, d-αA, Rm)和ζm~CN(0, d-αRm, B);ρ∈[0,1]表示信道ĥm和hm以及ĝm和gm的相关系数,这里假设中继节点与2个源节点间信道的相关系数相同.由Jakes模型,有ρ=|J0(2πfdτ)|,其中,J0(·)表示第1类零阶贝塞尔函数,fd表示多普勒频移,τ表示中继选择时刻和数据传输时刻的信道时延.当ρ=1,表示理想的信道状态,即中继选择时刻和数据传输时刻的信道状态保持不变;当ρ < 1,表示信道状态信息产生了过时,即中继选择时刻和数据传输时刻的信道状态不一致.
为了达到端到端的信噪比最大,最优中继Rm*需满足
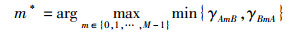
|
(8) |
但如前所述,实际中由于网络调度等原因极易导致选择的最优中继不能进行数据转发,因此需要选择第2、第3、或者统称为第N最优中继Rm*,使之满足
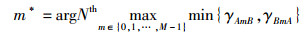
|
(9) |
由式(9) 可见,第N最优中继选择算法主要基于信道的信噪比,在实际中,该算法可采用分布式中继选择来实现,其具体步骤如下:首先,2个源节点向所有中继节点广播导频信号;每个中继节点收到导频信号后,估计自己与2个源节点的信噪比,找出其中的较小值,并以此设定定时器的初始值,即定时器的定时时间与该信噪比成反比;接着,各中继点启动定时器.若某个中继定时器的定时时间结束,即发送1个信标信号,系统一旦监听到已发送了N个信标信号,那么,发送第N个信标信号的中继点即为第N最优中继.于是,第N最优中继对接收到的数据进行放大转发至节点A和B,而其他中继保持沉默状态.
3 过时信道状态下的系统中断性能为了研究第N最优中继选择算法在过时信道状态下的中断率性能,首先分析中继选择时刻信噪比的概率密度函数和以它为条件的数据传输时刻信噪比的条件概率密度函数,从而确定数据传输时刻信噪比的概率密度函数,以此给出系统中断率下界的闭式表达及其在高信噪比下的近似值.
令Z=min(γAmB, γBmA)表示中继选择时刻的两条路径上的信噪比较小值,Y=min(γ′AmB, γ′BmA)表示数据传输时刻两条路径上的信噪比较小值,则Z与Y均是独立同分布的. Z的分布函数为
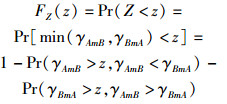
|
(10) |
其中
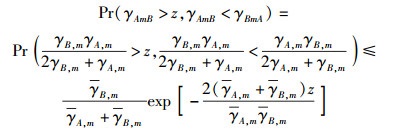
|
(11) |
同理,
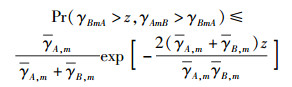
|
(12) |
把式(11) 和式(12) 代入式(10) 可得Z的分布函数的下界
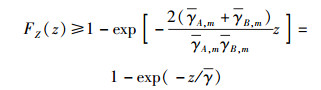
|
(13) |
其中γ=(γA, mγB, m/[2(γA, m+γB, m)].对式(13) 微分,可得Z的概率密度函数下界:
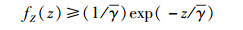
|
(14) |
由式(14) 可知,Z近似服从指数分布.
于是,根据文献[10]的定理2.11,对各个中继对应的Z从大到小进行排序,其中第N个Z的概率密度函数fZ(N)(x)为
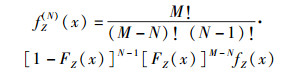
|
(15) |
其中中继点的个数M即为进行排序的总个数,将式(13) 和式(14) 代入式(15),可得
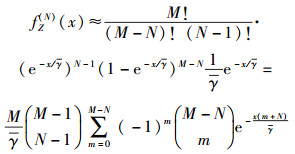
|
(16) |
以中继选择时刻的信噪比Z为条件,数据传输时刻信噪比Y的条件概率密度函数为[11]
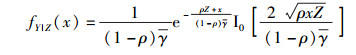
|
(17) |
其中I0(·)表示零阶修正贝塞尔函数,由式(16) 和式(17) 可得到数据传输时刻信噪比Y的概率密度函数为
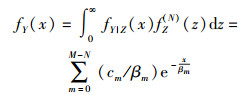
|
(18) |
其中:cm=(-1)m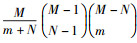
基于上述结论,下面推导所提算法的中断率.根据中断率的定义,当传输路径A→Rm→B的信噪比γ′AmB,或者路径B→Rm→A的信噪比γ′BmA低于门限值γth=22υ-1时,系统发生中断,同时由式(18) 可得过时信道状态信息下系统中断率的下界为
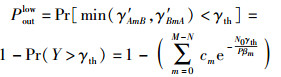
|
(19) |
其中γth表示系统持续工作所需要达到的最小信噪比.根据香农公式有,系统持续工作所需要达到的最小传输速率υ=(1/2) lb(1+γth),如果双向中继链路中任有1条的传输速率小于υ,则认为系统中断.根据泰勒级数展开近似式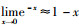
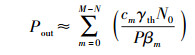
|
(20) |
对第N最优中继选择算法进行仿真,取各节点的发射功率相同,即PA=PB=Pm=P,中继点个数M=10,路径损耗α=3,归一化距离dA, Rm和dRm, B分别取0.2和0.8,门限γth=0 dB.
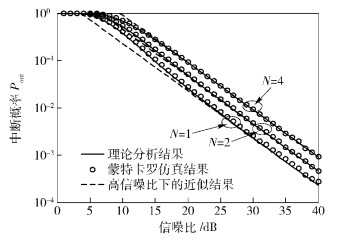
图 1给出了信道状态信息出现过时(ρ=0.5) 的系统中断率随信噪比变化的仿真曲线,N∈{1, 2, 4}.从图中可以明显看出:理论分析结果同蒙特卡罗仿真结果相重合,且在高信噪比下,中断率的近似表达结果能很好地逼近理论结果,进一步验证了理论分析结果的正确性.同时,随着N的增加,中断率性能有所恶化,且对于不同的N值,中断率曲线的斜率相同,这是由于当ρ < 1时机会双向中继系统的分集阶数为1.
|
图 1 中断率随信噪比变化的曲线 |
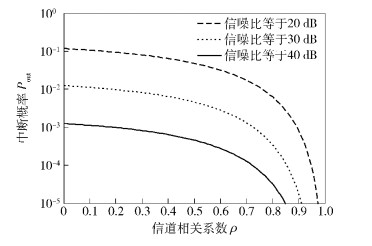
为了分析信道状态信息产生过时对系统中断率性能的影响,图 2示出了相同N值和不同信噪比下,即N=2、信噪比分别为20、30和40 dB时,系统的中断率性能随相关系数ρ变化的仿真曲线.从图 2可以看出,ρ值越小,也就是信道状态信息过时的情况越严重,系统的中断率就越大;ρ值越接近1,系统中断率就越小,系统性能大大改善,这是由于ρ=1对应着信道状态信息没有过时的理想情况.由此可见,信道状态信息是否过时对系统中断率性能的影响是极大的;另一方面,随着信噪比的增大,系统中断率性能也有所改善.
|
图 2 中断率随相关系数ρ变化的曲线 |
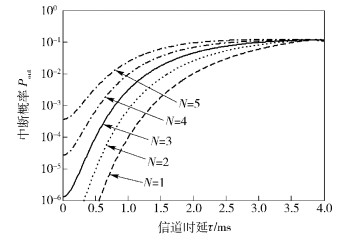
为了更直观地说明过时信道对系统中断率的影响,图 3给示了中断概率随信道时延τ变化的仿真曲线,其中信噪比为20 dB,多普勒频偏fd=100 Hz.从图 3可以看出,随着时延τ的增大,对应相关系数ρ值减小,即中继选择时刻信道和中继传输数据时刻信道的相关性减弱,中断概率总体呈增大趋势.特别地,当τ=4 ms时,对应相关系数ρ=0,表示信道完全不相关,此时不同N值对应的中断概率都最大.
|
图 3 中断率随时延τ变化的曲线 |
笔者对过时信道状态下机会双向中继协同通信系统的中继选择算法进行了研究.针对第1最优中继由于网络调度、负载平衡等原因,无法作为当前任务的中继点的情况,提出了一种第N最优中继选择算法,给出系统中断率下界的闭式表达及其在高信噪比下的近似值.理论和仿真结果表明,所提算法的理论分析结果同蒙特卡罗仿真结果相重合,且在高信噪比下,中断率的近似值能很好地逼近理论值,从而验证了所提算法的正确性.
| [1] | Bletsas A, Khisti A, Reed D P, et al. A simple cooperative diversity method based on network path selection[J].IEEE J Sel Areas Commun, 2006, 24(3): 659–672. doi: 10.1109/JSAC.2005.862417 |
| [2] |
崔海霞, 韦岗, 张军. 一种机会协作重传协议及其性能分析模型研究[J]. 电子学报, 2010, 38(10): 2410–2415.
Cui Haixia, Wei Gang, Zhang Jun. An opportunistic cooperative retransmission protocol and the research of its performance analytical model[J].Acta Electronica Sinica, 2010, 38(10): 2410–2415. |
| [3] |
吴皓威, 曹耘瑕, 李恩玉, 等. 基于竞争策略和ARQ的增强型放大转发协议[J]. 北京邮电大学学报, 2013, 36(6): 27–31.
Wu Haowei, Cao Yunxia, Li Enyu, et al. Incremental amplify-and-forward protocol based on competition scheme and ARQ[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(6): 27–31. |
| [4] | Rankov B, Wittneben A. Spectral efficient protocols for half-duplex fading relay channels[J].IEEE J Sel Areas Commun, 2007, 25(2): 379–389. doi: 10.1109/JSAC.2007.070213 |
| [5] |
李勇, 张翔, 彭木根, 等. 瑞利双向中继信道的功率分配及中继位置选择[J]. 北京邮电大学学报, 2012, 35(2): 94–98.
Li Yong, Zhang Xiang, Peng Mugen, et al. Power allocation and relay location selection for Rayleigh two-way relay channel[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(2): 94–98. |
| [6] | Shi Jingjing, Ge Jianhua, Li Jing. Low-complexity distributed relay selection for two-way AF relaying networks[J].IET Electron Lett, 2012, 48(3): 169–172. doi: 10.1049/el.2011.3527 |
| [7] | Li Enyu, Yang Shizhong, Wu Haowei. A source-relay selection scheme in two-way amplify-and-forward relaying networks[J].IEEE Commun Lett, 2012, 16(10): 1564–1567. doi: 10.1109/LCOMM.2012.081612.121389 |
| [8] | Hwang K, Ju M, Alouini M. Outage performance of opportunistic two-way amplify-and-forward relaying with outdated channel state information[J].IEEE Trans Commun, 2013, 61(9): 3635–3643. doi: 10.1109/TCOMM.2013.071213.120826 |
| [9] | Vicario J L, Bel A, Lopez-Salcedo J A, et al. Opportunistic relay selection with outdated CSI: outage probability and diversity analysis[J].IEEE Trans Wireless Commun, 2009, 8(6): 2872–2876. doi: 10.1109/TWC.2009.081561 |
| [10] | Güngör M, Bulut Y, Calik S. Distributions of order statistics[J].Applied Mathematical Sciences, 2009, 3(16): 795–802. |
| [11] | Vicario J, Anton-Haro C. Analytical assessment of multi-user vs spatial diversity trade-offs with delayed channel state information[J].IEEE Commun Lett, 2006, 10(8): 588–590. doi: 10.1109/LCOMM.2006.1665119 |


