2. 电子科技大学 通信学院, 成都 611731
通过分析频率跳变中的转移概率特性, 对比了常规跳频、差分跳频的几种典型实现方式中跳频图案变化的状态转移特性, 分析结果表明, 转移概率对跳频系统抗截获和干扰性能有重要影响, 差分跳频虽能提供基于信息数据的更随机化跳频图案, 但就转移概率特性而言与常规跳频差别不大, 且差分转移阶数较低时其抗干扰性能不如常规跳频.所提基于跳频转移概率分析的跳频图案分析和干扰方法更简单实用, 且可根据性能指标和实际转移概率分布进行干扰策略的动态调整.
2. School of Communication and Information Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
Analysis of transition feature of frequency hopping (FH) sequence was given for traditional frequency hopping (TFH) and correlated hopping enhances spread spectrum (CHESS) or differential frequency hopping (DFH) systems. It demonstrates that the transition probability distribution (TPD) of FH is very important for performance of both TFH and CHESS system, and that though CHESS can provide non-fixed frequency hopping pattern (FHP) for better anti-interceptions, its anti-jamming performance might be lower than that of TFH systems if its fan-out is not big enough. The proposed method TPD based FHP analysis and interference method does not require exact FHP, therefore it is much easier to implement; furthermore jamming strategy thus jamming efficiency can be dynamically adjusted according to some constraints or obtained TPD on-site.
跳频是一种“躲避式”抗干扰方法[1].跳频通信有传统跳频(TFH,traditional frequency hopping)和相关/差分跳频(DFH,differential frequency hopping/CHESS,correlated hopping enhances spread spectrum)两种技术,前者数据与跳频图案(FHP,frequency hopping pattern)无关,后者使用数据控制跳频序列[2-4].现有文献大多关注跳频图案产生,保证其良好的随机性能,包括汉明自相关参数、汉明互相关参数、平衡特性参数等[3-7],仅有部分讨论DFH序列的平衡性、极限分布等的文献涉及转移概率分析[3, 5-6].而跳频通信产生的跳频图案即跳频序列本质上是一种马尔可夫过程,有其特定的转移概率分布(TPD,transition probability distribution)特性,其与跳频系统的抗截获或抗干扰性能的关系未见报道.为此,笔者针对TFH和DFH系统的跳频序列的转移概率特性进行分析并给出新的侦听、干扰方法和初步性能分析.
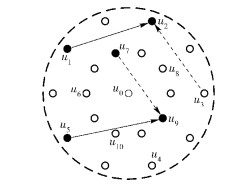
1 系统模型1.1 跳频组网考虑一个区域中N个用户构成的跳频网.这些用户可以采用集中式控制或者分布式控制方式进行组网,如图 1所示.
|
图 1 典型FH组网拓扑 |
集中式控制方式使用同一跳频图案进行通信,并由主控节点负责信道资源的访问分配,数据传输过程可以分为2种会话:一是主控节点进行多播通信;二是主控节点和某一个从节点进行单播通信,整个网络中,只允许一个会话.
分布式控制方式基于自组织形式,可以使用相同或不同的跳频图案进行分布式接入控制和通信.当所有节点共享一个跳频图案时,只允许1个会话;当所有节点各自拥有独立跳频图案时,则最多能建立⌋N/2」个会话,而且每个会话的收方不能成为其他会话的收方,比如,图 1中u1向u2发送时,u2不能接收其他用户如u3发送的信息,而u5向u9发送时,u7不能向u9发送.
1.2 跳频图案产生跳频图案是跳频通信的核心. TFH和DFH系统的跳频图案产生方法简单介绍如下.
1.2.1 TFH系统的跳频图案设跳频频率集大小为N(通常选择N=2W,W>0),二进制伪随机序列用c(n)∈[0,1]表示(c(0) 表示序列第1个值),每跳频率在频率集的对应下标h(n)为
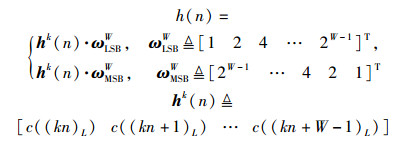
|
(1) |
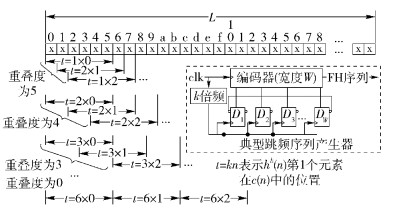
其中:L为跳频序列周期;(τ)L表示τ对L取模;1≤k≤W表示相邻hk(n)的不重叠元素个数(跳频周期与c(n)周期之比),当k=W时无重叠. 图 2给出了跳频序列产生原理和W=6,k分别为1、2、3、6,即重叠度分别为5、4、3、0时,前3个hk(n)中第1个元素在c(n)中的位置t=kn.
|
图 2 典型FH序列产生原理 |
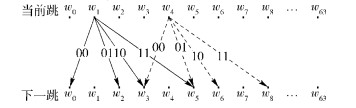
DFH系统用频率转移来携带数据(见图 3),没有固定跳频图案.频率转移由跳频函数给出,即
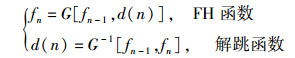
|
(2) |
|
图 3 DFH系统原理 |
该函数为一可逆函数.其中:
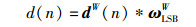
|
(3) |
dW(n)为宽度为W比特的二进制数据向量,W为每跳可携带最大比特数,而fn-1转到下一跳频率fn的最大可能支路数即扇出系数fout≤2W≤N.式(2) 中的跳频函数G(fn-1, d)可以看作一种时频网格编码.
不失一般性,仅讨论以下差分跳频函数:
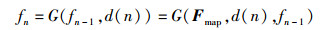
|
(4) |
其中G(F, r, c)表示下一跳的频率为矩阵Fmap中的第r行第c列对应元素所对应的频率. 2种Fmap为
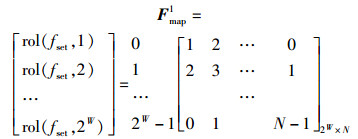
|
(5) |
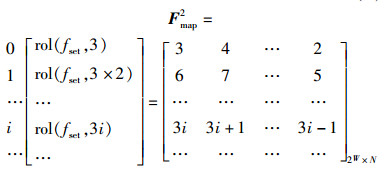
|
(6) |
其中:fset=[0, 1, …, N-1],rol(v, k)将v循环左移k次.以式(5) 为例,当d(n)=1,fn-1=7时,fn=8.
2 跳频图案性能2.1 转移概率分析对任意随机序列,总可以看成一个马尔可夫序列以进行转移概率分析.
2.1.1 TFH系统从h(n)到h(n-1) 有2k个等概率转移状态,有
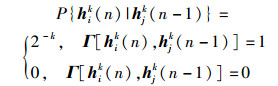
|
(7) |
其中Γk[x, y]=1表示x的左W-k位与y的右W-k位相同,0≤i, j≤2W-1.当W=3,k=1、k=2时,一阶转移矩阵分别为
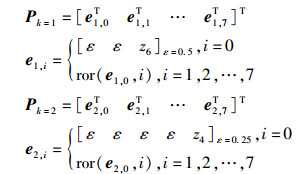
|
(8) |
其中:ror(v, k)将v循环右移k次,zm表示有m个0元素构成的向量.
2.1.2 DFH系统当N=13时,Fmap选用式(5) 或者式(6) 的一阶转移概率矩阵分别为
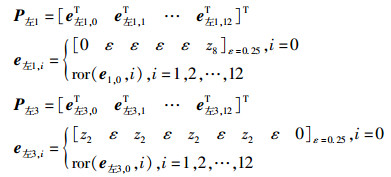
|
(9) |
图 4分别给出了TFH和DFH系统的跳频序列转移概率矩阵的图像表示,图中横轴对应当前跳,纵轴对应下一跳,“黑点”表示转移概率为非零.
|
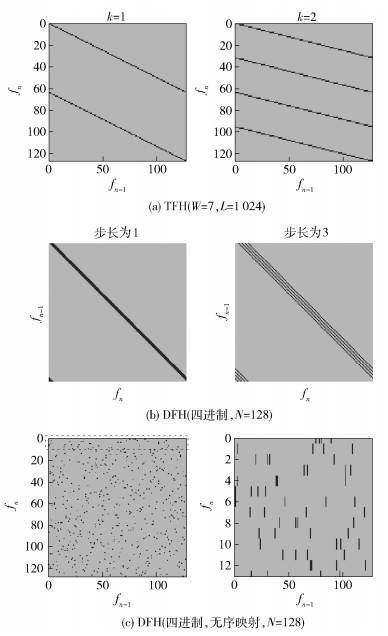
图 4 跳频序列的TPD图像展示 |
图 4(a)所示为TFH系统下W=7、L=1 024时,k为1和2的转移概率;图 4(b)所示为DFH系统W=2、N=128时,式(9) 的2种转移概率;图 4(c)所示为四进制DFH系统的一种随机映射图的转移概率,右图为左图虚框区域的局部放大.
由图 4可以看出,从跳频转移概率角度看,特定跳频源的跳频转移支路及其概率分布总可以通过统计得到,而无需考虑其跳频原理及其跳频图案本身.
2.2 平衡性平衡性是指跳频序列中频率分布的等概率性.
根据式(7) 容易证明,TFH只要伪随机码序列满足平衡性要求,而DFH系统只要数据序列满足平衡性要求,跳频频率一定满足平衡性要求,即对任意W和k,平稳分布存在且为
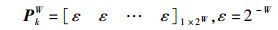
|
(10) |
由于频率映射函数h(n)的概率分布特性,跳频序列的汉明互相关由h(n)的汉明互相关给出,即
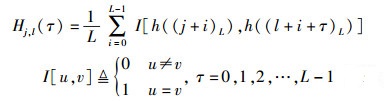
|
(11) |
其中L为跳频序列的周期长度.当j=l时,式(11) 为h(n)的汉明自相关.
显然,汉明自相关峰值与最大旁瓣之比Ha越大说明自相关峰越尖锐,而汉明自相关峰值和最大汉明互相关比值Hm越大则汉明互相关特性越好. Ha和Hm的计算式为

|
(12) |
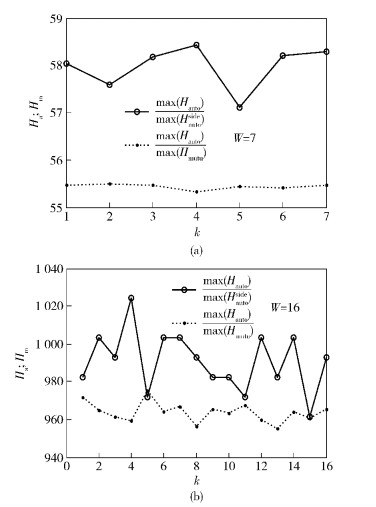
图 5给出了TFH系统50种L=1 024的随机序列下W分别为7和16时,Ha和Hm均值与k的关系示意.可知,汉明自相关/互相关特性与k无关,且W越大越好,这与状态数以W指数增加是一致的.
|
图 5 TFH图案的汉明相关性 |
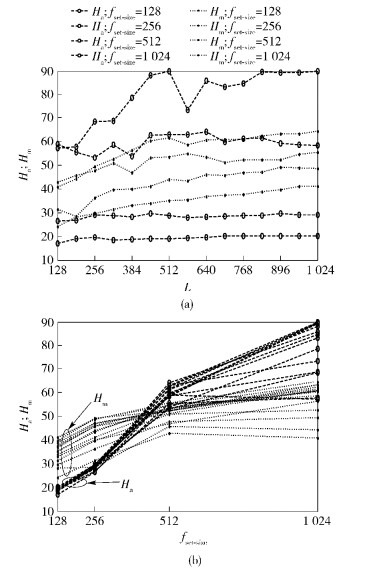
DFH系统没有固定的FHP,但作为对照,图 6给出了跳频集合大小N=[128:64:1 024],分段长度L=[128:64:1 024]时,50个不同跳频序列段的Ha和Hm均值与N和L的关系.可知,Ha和Hm与L关系不大,但随N增加而增加,这与TFH系统中增加W时情形一致.
|
图 6 DFH序列的汉明相关性 |
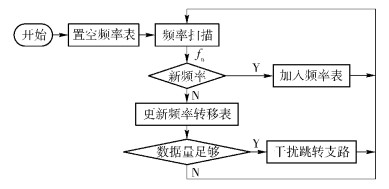
图 7所示为适用于TFH和DFH系统的干扰流程,其核心是跳频转移概率分析,以建立跳频转移概率表;干扰阶段可根据当前跳频率fn,查阅跳频转移概率表对其中非零值对应的全部频率或较高转移概率的跳频转移支路进行干扰.
|
图 7 基于转移概率的跳频干扰流程 |
单会话情形下跳频转移表直接反映了跳频转移规律.为此,对TFH而言,跳频转移支路数仅与k有关,其跳频转移支路数为B=2k≤N;而对DFH而言,跳频转移支路数仅由扇出系数fout=2W,即每跳可携带比特数W决定.设最大跳频支路数为B,选择其中的Bj(Bj≤B)个支路,则干扰阻塞率为Bj/B.
显然,对攻方而言,实际转移支路数越多难度越大;而对守方而言,当跳频频率和频率集大小确定后,提高B意味着提高TFH的频率发生器时钟或者降低DFH系统的低跳频序列汉明距.
3.2 多会话场景下的干扰性能在分布式模式下一般会同时存在多个会话,因而跳频截获得到的转移概率不再是式(8) 等的简单情形,而是多个会话的“联合”转移概率.
不失一般性,仅对频率集大小为N=128的四进制DFH进行分析.假设跳频网中有2个会话,s1和s2使用相同跳频周期T=1 ms,每跳传输8 bit,并考虑2种双会话情形.
情形1 会话s1中的发送方是网络中级别较高的节点,如战术场景下.每256跳为一组,会话s1以概率p1>0.5随机发送,而会话s2的发送概率p2 < 0.5.
情形2 会话s1处于连续发送过程中,而s2只是偶尔发送,可看作情形1的特例,即p1=1.
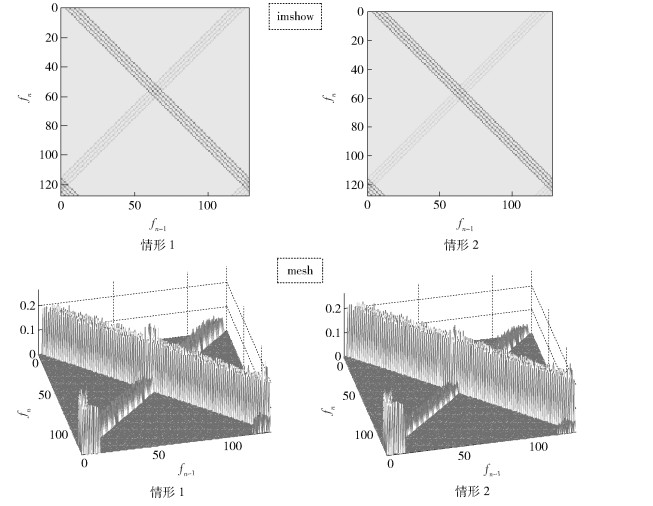
图 8给出了情形1(p1, p2)=(0.90, 0.20),情形2(p1, p2)=(1.0, 0.30) 时的转移概率图像2D(imshow)和3D(mesh)显示,会话s1、s2频率集相同,但Fmaps1各行与Fmaps2对应行的顺序相反,图中颜色越深,概率越大.
|
图 8 多会话的2种情形下的TPD示意 |
由图 8可以看到,虽然多个会话的跳频序列混叠在一起时转移概率不能直接看出其跳频转移支路数,但当会话活动程度不同时,其转移概率大小与活动程度高度相关.据此,可基于概率统计结果动态地对跳频网的全部会话或较高活动性会话的全部或部分下一跳支路实施干扰以提高干扰效率.
4 结束语从跳频转移概率的角度看,TFH与DFH没有本质不同,因而所提方法无需对跳频图案进行详细分析,实现简单.当跳频转移数fout不大时,干扰方总可较有效地进行干扰;而当fout较大时,可对多会话中活动性较高的下一跳频转移支路进行有针对性的干扰.总体干扰性能还可进行按需调节.
从守方角度,TFH系统和DFH系统均须提高整个跳频网的“整体”跳频转移支路数以降低风险,即以提高TFH的复杂度或降低DFH系统的汉明距或者尽量使所有电台活动程度均衡从而增加被截获的概率和跳频网络的整体功耗,也意味着降低抗毁性/生存性.
| [1] |
冯涛, 袁超伟. 跳频信号的时频分析新方法[J]. 北京邮电大学学报, 2010, 33(3): 10–14.
Feng Tao, Yuan Chaowei. A method of time-frequency analysis for frequency-hopping signals[J].Journal of Beijing University of Posts and Telecommunications, 2010, 33(3): 10–14. |
| [2] | 屈晓旭. 抗干扰抗截获差分跳频技术研究[D]. 武汉: 华中科技大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10487-1011110092.htm |
| [3] | 陈智. 差分跳频通信系统的性能分析[D]. 成都: 电子科技大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10614-2006113493.htm |
| [4] |
董彬虹, 李少谦, 史锋旗. 一种差分跳频码发生器的构造方法[J]. 电子与信息学报, 2010, 32(4): 816-820.
Dong Binhong, Li Shaoqian, Shi Fengqi. A differential frequency hopping code generator construction method[J]. 2010, 32(4): 816-820. http://jeit.ie.ac.cn/CN/Y2010/V32/I4/816 |
| [5] |
李天昀, 许漫坤, 葛临东. 相关跳频转移函数的双随机矩阵模型及其应用[J]. 电子与信息学报, 2007, 29(9): 2182–2186.
Li Tianyun, Xu Mankun, Ge Lindong. Doubly stochastic matrices model of DFH G-function and its application[J].Journal of Eletronics & Information Technology, 2007, 29(9): 2182–2186. |
| [6] |
周义明, 周正. 协作频谱感知中感知用户的选择与信噪比估计算法[J]. 北京邮电大学学报, 2013, 36(6): 108–112.
Zhou Yiming, Zhou Zheng. The algorithm about secondary users selection and SNR estimation in cooperative spectrum sensing[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(6): 108–112. |


