2. 哈尔滨工程大学 自动化学院, 哈尔滨 150001
提出了一种T细胞免疫模糊控制方法.首先利用免疫过程中T细胞浓度调节的原理, 在免疫反馈控制数学模型中引入T细胞调节因子, 再利用模糊控制器逼近T细胞调节因子表示的非线性函数.该方法与传统比例—积分控制和免疫反馈控制相比, 能有效抑制负载扰动对电动机转速、电磁转矩输出和电流输出的影响, 具备优良的抗系统误差能力和转速跟随能力.永磁同步电动机(PMSM)调速系统的应用结果表明该方法具备一定可行性.
2. Automation College, Harbin Engineering University, Harbin 150001, China
A method of T immune fuzzy control was proposed. The T immune cell regulatory factor was introduced in the mathematical model of feedback control by applying the principle of immune T cell concentration regulation. And the nonlinear function of the fuzzy controller was used to approximate T cell regulatory factor. Compared with traditional PI control and immune feedback control, it can effectively suppress the effect of load disturbance on speed, electromagnetic torque output and current output. So it has excellent capability of resistance to systematic errors and speed following. Application on permanent magnet synchronous motor (PMSM) speed system shows the practicability of the proposed method.
永磁同步电动机(PMSM,permanent magnet synchronous motor)一般采用比例-积分-微分(PID,proportional integral derivative)控制,其抗干扰和参数摄动鲁棒性不够理想,难以得到满意的动态特性. Takahashi等[1]提出了免疫反馈控制方法, 应用于直流电动机传动系统中;Ren等[2]设计了一种用于液压弯曲控制的免疫模糊控制器;Qin等[3]提出了一种模糊免疫PID控制方法,用于直流力矩电动机的脉宽调制调速系统;Song等[4]和Yuan等[5]采用模糊策略逼近免疫PID算法的控制参数;Shih等[6]提出了一类混沌系统的自适应反推模糊免疫控制器;王等[7]采用混沌方法,对汽轮机调速系统中的模糊免疫PID控制器参数进行优化;王等[8]利用免疫反馈机理,自适应调整永磁交流伺服系统中的单神经元PID控制器参数;Lin等[9]提出了一种免疫模糊滑模控制器,能有效改善滑模控制的“抖振”,具有较强鲁棒性.
上述研究未见对免疫反馈控制数学模型的本质改进,多见与其他方法的混合研究.笔者在免疫反馈控制器中引入T细胞调节因子,提出T免疫模糊控制方法.该方法是将B细胞的浓度作为控制状态量,依据生物机体T细胞响应影响B细胞浓度调节的规律,利用模糊控制器对T细胞调节因子进行模糊逼近.该方法用于PMSM调速系统,可获得良好的鲁棒性和转速跟随能力.
1 免疫反馈控制免疫反馈控制器[1]是借鉴生物系统的免疫机理而设计出的一种非线性控制器.第k代B细胞的浓度为
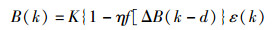
|
(1) |
其中:表示T抑制细胞(TS,T suppression cell)与T辅助细胞(TH,T helper cell)作用的比例系数K=k1; η=k2/k1,k1为刺激因子,k2为抑制因子;ΔB(k)为B细胞浓度变化;d为免疫响应的延迟时间;f[·]为一非线性函数,与机体内B细胞的浓度和浓度变化有关;ε(k)为第k代抗原的数量.
考虑到机体免疫反馈过程的不同阶段,假设λ为选择不同阶段的免疫调节作用,免疫促进阶段λ=-1,免疫抑制阶段λ=1,免疫稳定阶段λ=0.
若以抗原的数量ε(k)作为偏差e(k), B细胞的浓度B(k)作为控制状态u(k), 则免疫反馈控制规律为
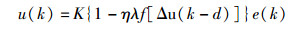
|
(2) |
由式(2) 可获得式(3) 描述的T免疫控制系统方程.

|
(3) |
其中:T(k)为免疫控制过程中的T细胞调节因子,由免疫调节阶段选择λ、控制偏差e(t)和免疫控制调节函数f[Δu(k-d)]以乘积的形式表示;控制状态u(k)为免疫控制过程中的B细胞浓度,控制系统当前状态u(k)受到控制参数K、η和T细胞调节因子的影响.
2.2 T细胞调节因子T细胞调节是一个非常复杂的非线性过程,T(k)通过选择合适的非线性函数f[Δu(k-d)]以及设计参数,能够很好模拟免疫控制规律中的非线性特性.通过比较,选择式(4) 中的非线性函数来模拟T细胞调节作用,a为抗体浓度作用系数,设计参数a=10.
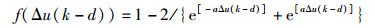
|
(4) |
由式(3) 和式(4) 可获得T细胞调节因子完整描述:
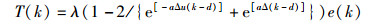
|
(5) |
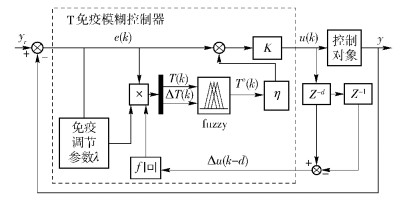
利用模糊控制器可逼近任意的非线性函数特性,对非线性环节T(k)进行模糊逼近.所构成的T免疫模糊控制器结构如图 1所示.
|
图 1 T免疫模糊控制结构 |
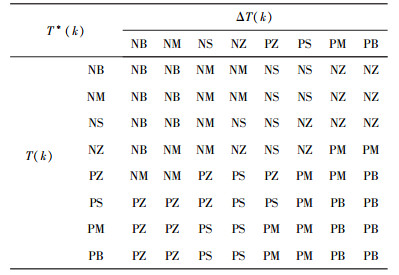
图 1中模糊控制器有T(k)和ΔT(k)两个输入量和一个输出量T*(k),输出量是T细胞浓度调节函数,T*(k)=fuzzy[T(k), ΔT(k)]. y为控制系统输出,Z-1、Z-d分别为1维和d维离散变换. T免疫模糊控制器的模糊逻辑数值分布见表 1.其中NB、NM、NS、NZ、PZ、PS、PM、PB分别表示“负大”、“负中”、“负小”、“负零”、“正零”、“正小”、“正中”和“正大”这8个模糊子集.
|
|
表 1 模糊逻辑 |
输入量T(k)和ΔT(k)分别被8个模糊子集定义在(0,1) 和(0,2.5) 数值区间,输出量限定在(0,0.5) 的数值区间内,隶属度函数选用三角函数,解模糊采用centroid算法.
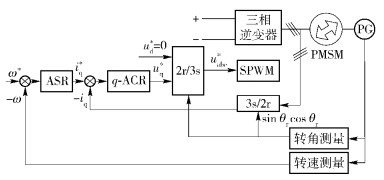
3 PMSM调速系统计算机仿真采用图 2中的PMSM交流调速系统,PMSM定子由三相正弦波脉宽调制(SPWM,sinusoidal pulse width modulation)逆变器供电,转子位置传感器PG检测电动机转子的转速ω和转角θr.内环为自动电流调节器(ACR,automatic current regulator),采用比例-积分(PI,proportional integral)控制器进行控制;外环为自动转速调节器(ASR,automatic speed regulator),分别采用T免疫模糊控制、PI控制或免疫反馈控制进行对比研究. ASR和ACR得到定子电压的转矩分量uq*,在定子电压励磁分量ud*=0的条件下经二相旋转/三相静止坐标变换2r/3s,得到SPWM调制器的三相电压调制信号.
|
图 2 PMSM调速系统 |
利用Matlab/Simulink7.12.0进行计算机仿真. T免疫模糊控制器作为PMSM调速系统的速度外环,控制参数K=1,η=0.2;电流内环采用PI控制器进行调节,比例控制参数kp=10.7, 积分控制参数ki=10. PMSM双闭环调速系统空载启动,给定转速3 500 r/min,0.1 s时突加负载4 N·m.
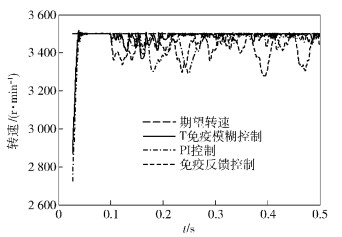
由图 3可见,T免疫模糊控制的PMSM转速上升平稳、输出稳定,0.05 s时PMSM调速系统达到稳定状态,控制响应无超调量和稳态误差;与速度外环采用PI控制或免疫反馈控制相比,0.1 s时突加负载4 N·m,转速开始略有下降、出现波动,但随即约在0.22 s时重新恢复到给定值,此后转速控制响应输出相对稳定、无稳态误差.而其他2种控制器0.1 s加入负载后,存在转速波动和转速误差. T免疫模糊控制的鲁棒能力较强,转速跟踪性能较好.
|
图 3 转速控制响应 |
由图 4可见,0.05 s时T免疫模糊控制器控制的PMSM电磁转矩输出围绕0值附近小幅波动;0.1 s时突加负载4 N·m,电磁转矩输出瞬间跳变到5 N·m,此后电磁转矩输出跟随负载转矩,在4 N·m附近的数值区间波动,无周期性规律.在突加负载PMSM转速出现波动的0.1~0.22 s时间内,T免疫模糊控制器控制的PMSM电磁转矩输出无明显变化,鲁棒能力较强.
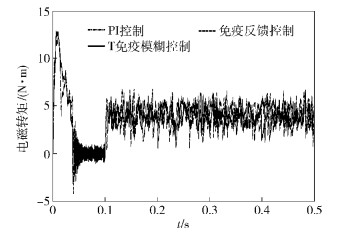
|
图 4 电磁转矩输出 |
由图 5可见,与速度外环采用PI控制器或免疫反馈控制器相比,0.1 s时突加负载4 N·m,T免疫模糊控制器控制的PMSM定子电流励磁分量id和定子电流转矩分量iq瞬间输出值均小于20 A,能一定程度地克服PMSM突加负载、定子电流输出瞬间过大对系统造成的冲击;PMSM定子电流转矩分量iq在0.1~0.22 s时间内存在较大的电流波动,0.22 s后PMSM系统输出处于稳态,此时定子电流转矩分量iq输出值减小、电流波动改善明显.
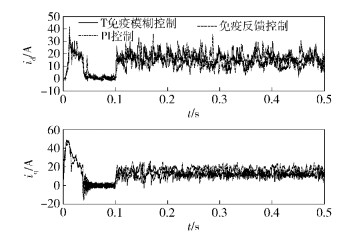
|
图 5 定子电流输出 |
本研究基于生物免疫系统中的T细胞调节免疫机理,在免疫反馈控制器中引入T细胞调节因子,再利用模糊控制器可逼近任意的非线性函数特性,对非线性函数特性明显的T细胞调节因子进行模糊逼近,构成一种T免疫模糊控制器.
仿真结果表明,与传统的PI控制器和免疫反馈控制器相比,T免疫模糊控制器具有良好的转速跟随能力,能在较短时间内有效克服突加负载对PMSM转速和电磁转矩输出的影响,有效抑制负载扰动对PMSM定子电流转矩分量的影响,输出值减小、电流波动改善明显,鲁棒性好.
T免疫模糊控制器作为一种新型控制器,应用于高精度、高准确性的控制环节,以及PMSM转速跟随能力要求较高的调速系统,具有一定的实际应用价值.
| [1] | Takahashi K, Yamada T. Application of an immune feedback mechanism to control systems[J].JSME International Journal, Series C, 1998, 41(2): 184–191. doi: 10.1299/jsmec.41.184 |
| [2] | Ren Xinyi, Du Fengshan, Huang Huagui, et al. Application of improved fuzzy immune PID controller to bending control system[J].International Journal of Iron and Steel Research, 2011, 18(3): 8–33. |
| [3] | Qin Li, Huang Weigang, Zhou Shili, et al. PWM speed regulating system of DC torque motor based on fuzzy immune-PID control source[J].Applied Mechanics and Materials, 2012, 466-467: 1129–1134. |
| [4] | Song Rongrong, Ma Weihua, Chen Zili. Study on improved fuzzy immune PID controller for maglev transportation system with track irregularity[J].Applied Mechanics and Materials, 2013, 423-426: 2825–2831. doi: 10.4028/www.scientific.net/AMM.423-426 |
| [5] | Yuan Guili, Liu Jizhen. The design for feed water system of boiler based on fuzzy immune smith control[J].Journal of Computers, 2012, 7(1): 278–283. |
| [6] | Shih K S, Li T H, Tsai S H. New nonlinear controller for a class of chaotic systems based on adaptive backstepping fuzzy immune control[J].Mathematical Problems in Engineering, 2011, 28(5): 1–10. |
| [7] |
王爽心, 姜妍, 李亚光. 基于混合混沌优化策略的汽轮机调速系统模糊免疫PID控制[J]. 中国电机工程学报, 2006, 26(11): 70–74.
Wang Shuangxin, Jiang Yan, Li Yaguang. Fuzzy immune PID control based on hybrid chaos optimization strategy of turbine speed control system[J].Chinese Society for Electrical Engineering, 2006, 26(11): 70–74. doi: 10.3321/j.issn:0258-8013.2006.11.014 |
| [8] |
王科, 刘新正. 免疫单神经元PID控制在永磁交流伺服系统中的应用[J]. 西安交通大学学报, 2010, 44(4): 76–81.
Wang Ke, Liu Xinzheng. Immune single neuron PID control in permanent magnet AC servo system[J].Journal of Xi'an Jiaotong University, 2010, 44(4): 76–81. doi: 10.7652/xjtuxb201004017 |
| [9] | Lin Wenbin, Chiang H K, Chung Y L. The speed control of immune-fuzzy sliding mode controller for a synchronous reluctance motor[J].Applied Mechanics and Materials, 2013(300-301): 1490–1493. |