提出了一种基于信号理论和网格化的尺度不变特征变换(SG-SIFT)光学遥感图像配准算法.根据高斯差分尺度空间中各图像层间的频域关系设定各图像提取特征点的数目, 使特征点在尺度域上分布均匀; 再将各图像层网格化, 使特征点在图像空间中分布均匀; 然后用一致性检测法剔除有明显错误的匹配对.实验结果表明, 利用SG-SIFT算法得到的特征点比尺度不变特征变换(SIFT)算法的特征点分布更均匀, 正确匹配对数目比均匀鲁棒尺度不变特征变换(UR-SIFT)算法均多17.47%, 且SG-SIFT算法的均方误差明显低于SIFT和UR-SIFT算法.
A new optical remote sensing image registration method signal gridding-scale invariant feature transform (SG-SIFT) based on signal theory and gridding is proposed. According to relationships among the image layers in the difference of Gaussians scale space, the feature points' number of each image is set in proportion to make the their distribution uniform in the scale space. In addition, a regular gridding method is introduced to achieve the well distribution of feature points in the image space. Then, error matching pairs are eliminated by a correspondence error checking. Statistical and visual results show that SG-SIFT is superior to standard scale invariant feature transform (SIFT) according to the feature points distribution, while the number of correct matching pairs from SG-SIFT is 17.47% more than that of uniform robust-scale invariant feature transform (UR-SIFT) in average and the evaluation indicator of root-mean square error confirms its superior performance to SIFT and UR-SIFT.
图像配准[1-2]作为图像处理的关键技术之一,是图像融合、超分辨率图像重建、三维图像重建等许多图像处理技术的重要组成部分,在航空、遥感、医疗等领域有着极其广泛的工程应用.
SIFT算法[3]是一种基于点特征的经典图像配准算法. SIFT特征描述符具有对图像灰度变化、旋转、缩放甚至仿射变换等保持不变性的优点,在同类描述子中具有很强的健壮性.由于辐射差异和获取影像传感器的不同,表征同一地区遥感影像间常常出现灰度差异、阴影和几何形变等,因此SIFT算法在遥感图像配准中应用广泛.近几年,针对SIFT算法应用于遥感影像的不足,提出了一些基于SIFT算法的提升方案[2-3]. 2011年Amin Sedaghat的UR-SIFT算法[4]解决了特征点分布不均的问题,但该算法各层图像的特征点数目与标准SIFT算法的特征点数目在比值上不相符,且随着尺度因子的增加,实际提取的特征点数目不能满足UR-SIFT的需要.
针对SIFT算法应用于遥感图像提取特征点分布不均和UR-SIFT的问题,提出了SG-SIFT算法.该算法使特征点在尺度域和空间域上分布均匀,尺度域上分布均匀保证了算法尺度不变性的发挥,空间域分布均匀保证了图像含局部形变时模型的求解;同时剔除了虚假匹配对,使配准结果更准确.
1 标准SIFT算法标准SIFT算法[3]由尺度空间极值点检测、特征点精确定位、特征点主方向确定和特征描述子生成4步组成.高斯拉普拉斯(LoG, Laplace of Gaussian)尺度空间由函数L(x, y, δ)表示,由变尺度因子的高斯函数G(x, y, δ)与图像I(x, y)卷积生成,
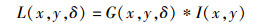
|
(1) |
其中:“*”表示在x和y方向上卷积,δ为尺度因子,高斯函数G(x, y, δ)表示为
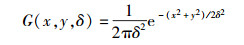
|
(2) |
SIFT算法用高斯差分(DoG, difference of Gaussians)尺度空间近似LoG尺度空间, 将LoG尺度空间中相邻图像相减得到DoG响应的图像序列:
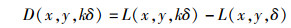
|
(3) |
根据Lowe[3],δ0=1.6,常数k=21/S, S为DoG尺度空间中每组可检测极值点的图像层数(一般取3).尺度空间中第o组的第s层的尺度因子δ(o, s)为
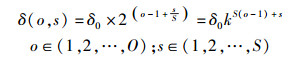
|
(4) |
其中:O为DoG尺度空间的组数(一般由图像尺寸决定),o为DoG尺度空间的组的索引,s为DoG尺度空间中各组内层的索引.
然后用非极大值抑制提取初始关键点[3];再用Taylor插值对提取的初始关键点进行精确定位,剔除在位置空间和尺度因子的任何方向偏移大于0.5的点、对比度较低和图像边缘的不稳定点,得到有精确位置的特征点;最后采用灰度直方图法确定特征点的主方向,生成SIFT特征描述符.
2 SG-SIFT算法2.1 SG-SIFT的特征点均匀分布由信号理论知,高斯函数G(x, y)与图像I(x, y)的空域卷积对应于高斯函数和图像的傅里叶变换Gw(u, v)和Iw(u, v)的频域乘积,即
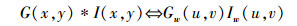
|
(5) |
可知,高斯函数的傅里叶变换仍是一个高斯函数,但变换前后的尺度因子成反比关系.高斯函数的宽度由尺度因子决定,即空域的尺度因子δ越大,则对应频域上的频带就越窄,滤掉的高频成分也越多.高斯函数与图像空域上卷积实际是对图像进行低通滤波,去除图像中的高频成分. LoG尺度空间是由尺度因子不断递增的高斯函数与源图像空域卷积得到的,因而随着组数和层数的增加,图像高频成分滤除的就越多;DoG尺度空间是对LoG尺度空间的近似,因此DoG尺度空间中也随着组数和层数的增加图像高频成分滤除越多. SIFT算法提取的特征点是表征图像突出特征和纹理特征的局部极值点,属于图像的高频成分.所以,从DoG尺度空间滤除高频成分少的图像中,得到的特征点数量自然就多.基于以上分析,设定从源图像DoG尺度空间提取的特征点数量为N,第o组第s层图像待提取的特征点数量Nos与该图像对应尺度因子的二次方成反比,即
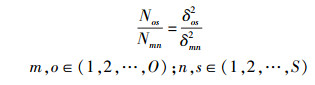
|
(6) |
其中: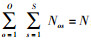
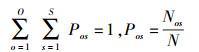
|
(7) |
当式(6) 中m=n=1时,即组数为1,层数也为1,由式(4)、式(6) 和式(7) 可得
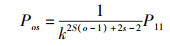
|
(8) |
将式(8) 代入式(7) 可得
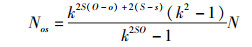
|
(9) |
式(9) 使DoG尺度空间的各尺度上均有一定数量的特征点,使算法尺度不变性不因某一尺度特征点数量过少而受影响.同时,设定的特征点数量N使SG-SIFT算法可以控制特征点总数量,避免了以下情况:特征点数量过多,增加特征描述符生成和特征匹配的计算量;特征点数量过少,变换模型求解不准确.因此,应根据实际需要设定特征点数量.
为保证特征点在空间域分布均匀,利用规则网格划分图像,再根据各网格内信息确定每个网格的特征点数量.首先,以网格内初始关键点数量和这些点的平均对比度作为该网格信息标准.网格内初始关键点数量越多,在一定程度上表明了该网格内纹理信息更丰富;初始关键点的对比度用该点DoG响应绝对值近似表征,初始关键点的平均对比度越高,则网格内的关键点更稳定.用i表示DoG尺度空间中某图像的网格索引,Gi表示第i个网格应提取特征点的数量,其表示为
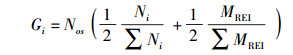
|
(10) |
其中:Ni和MREI分别为第i个网格内初始关键点的数量和平均对比度,∑ Ni和∑ MREI分别为该图像各网格初始关键点数量总和及平均对比度总和,2个1/2权值是经过反复实验得到的.根据Lowe[3],特征点数量对对比度敏感性较高,而对主曲率敏感性较低,所以在剔除不稳定关键点中着重使用了对比度. SG-SIFT算法提取均匀分布特征点的步骤如下.
输入:待处理的图像I;
输出:提取的特征点为P,P∈Rn×3.
1) 设定待提取特征点的数量N.设定特征点数量N为图像像素尺寸的0.4%[4].
2) 建立I的DoG尺度空间,并提取初始关键点.
3) 计算DoG尺度空间各组中各层图像的特征点数量Nos,并对第o组第s层图像做以下处理.
① 利用规则网格(100 pixel×100 pixel)对图像空间划分,并计算各网格分配特征点的数量Gi.
② 针对该图像第i个网格做以下处理:首先,用Taylor插值公式对网格内初始关键点精确定位,并计算各关键点的对比度|D(X)|,保留其值较高的前3Gi个关键点;然后,利用2×2的Hessian矩阵计算出剩余关键点主曲率的比值,剔除主曲率比值大于阈值[3]10的靠近边缘的不稳定点;最后,保留对比度较高的前Gi个关键点,即为特征点,放入特征点集合中.
2.2 虚假匹配点对的剔除在基准图像的SIFT特征描述符中查找与待配准图像的SIFT特征描述符欧氏距离中最邻近和次临近的,当两者距离比值超过某阈值时,则将待配准图像上的目标点与基准图像中最近的欧氏距离所对应的点视为匹配点对[5].通过该检索方法得到的匹配点对有可能是虚假匹配点对,为此,提出一种剔除虚假匹配点对的方案:首先利用所有匹配点对得到一个变换模型,再基于该变换模型用全局一致性检测法剔除虚假的匹配点对,最后利用已剔除虚假匹配的匹配点对重新计算变换模型.用式(11) 所示的仿射变换模型表示待配准图像中点(xi, yi)与基准图像中点(xr, yr)间的对应关系.
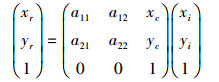
|
(11) |
其中a11、a12、a21、a22、xc和yc为仿射变换的参数.将待配准图像的特征点进行仿射变换,并计算与基准图像中的匹配点间的均方根误差(RMSE, root mean-square error),作为匹配点对虚假与否的标准. RMSE定义为
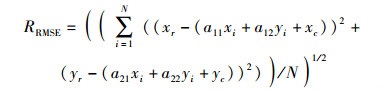
|
(12) |
其中N为所有匹配点对的数量,单位为pixel. RRMSE越大,说明待配准图像经模型变换后的特征点与基准图像中对应的匹配点相差越大,其中可能有虚假匹配点对,也说明了仿射变换模型求解的不准确;反之,计算的结果越精确.
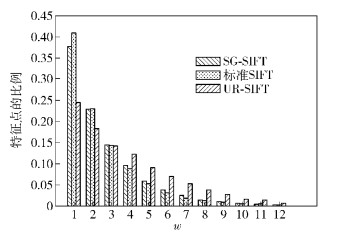
3 实验结果与分析3.1 SG-SIFT特征点分布的验证为验证SG-SIFT算法提取的特征点在尺度域和图像域分布均匀的可行性和有效性,采用了900 pixel×900 pixel的印度卫星遥感(IRS, Indian remote sensing)影像(http://www.satimagingcorp.com/gallery/irs-omen.html)按照2.1节方案进行相关实验,并与SIFT和UR-SIFT进行了对比. 图 1所示为UR-SIFT和SG-SIFT算法的特征点在尺度空间中的数量比值与标准SIFT算法提取的初始关键点数量比值的对比情况. 图 2所示为特征点在图像空间中分布的对比情况,其中SIFT算法提取的特征点在IRS图像中的分布如图 2(a)所示,SG-SIFT提取的特征点在IRS图像中的分布如图 2(b)所示.
|
图 1 SG-SIFT、标准SIFT和UR-SIFT提取IRS图像的特征点在尺度空间分布的对比 |

|
图 2 标准SIFT算法和SG-SIFT提取IRS影像(900 pixel×900 pixel)的特征点在图像空间的分布情况 |
图 1中,w(w=3o+s(1≤o≤4;1≤s≤3))代表DoG尺度空间中4组图像序列的中间3层,o和s分别为DoG尺度空间中组数和层数索引.由图 1可知,SG-SIFT的Pos比UR-SIFT更接近于SIFT;w较低时,SG-SIFT和SIFT算法的Pos比UR-SIFT的Pos高;w大于3以后,UR-SIFT的Pos超过了标准SIFT的Pos,但SG-SIFT与SIFT的Pos基本一致. w较小处对应DoG尺度空间中高斯滤波尺度因子δ较小处,即图像包含高频成分多,细节信息丰富,因而标准SIFT提取的初始关键点较多,Pos自然很大;随着w增加,高斯滤波尺度因子δ增大,图像的细节信息逐渐丢失,提取的初始关键点数量降低,因而Pos逐渐降低. SG-SIFT设定的特征点数量就是基于此,因而与标准SIFT提取初始关键点的Pos整体趋势更接近.另外,虽然标准SIFT提取初始关键点数量较多,且大于设定数量N,但在w较大处可能出现标准SIFT在图像上提取初始关键点的数量不能满足UR-SIFT要求分配数量,而SG-SIFT的比值与SIFT基本接近,故几乎不会发生上述情况.
由图 2可知,标准SIFT算法提取的特征点在图像灰度变化较大区域分布较多(见图 2(a)的区域Ⅰ和Ⅱ),在图像灰度变化较小的区域分布较少(如图 2(a)的区域Ⅲ);而SG-SIFT算法提取的特征点无论在图像灰度变化明显的区域还是在灰度变化平坦的区域分布都比较均匀,见图 2(b)的区域Ⅰ和Ⅱ以及区域Ⅲ;而且,SG-SIFT提取的特征点数量明显比标准SIFT提取的特征点数量少,在图像灰度变化明显的关键区域都有相应特征点分布,在图像灰度变化不大的区域特征点数量分布增加,这种控制特征点数量和分布的方式,既不让某些区域特征点数量特别多造成计算的负担,也不让某些区域特别少影响配准的精度.
3.2 SG-SIFT算法配准光学遥感影像为验证SG-SIFT算法用于光学遥感影像配准的有效性,采用了以下测试数据:SPOT5多光谱影像、IKONOS多光谱影像、QuickBird多光谱影像和WorldViewII多光谱影像,其中前3种是北京市遥感影像,最后一种是杭州市遥感影像.
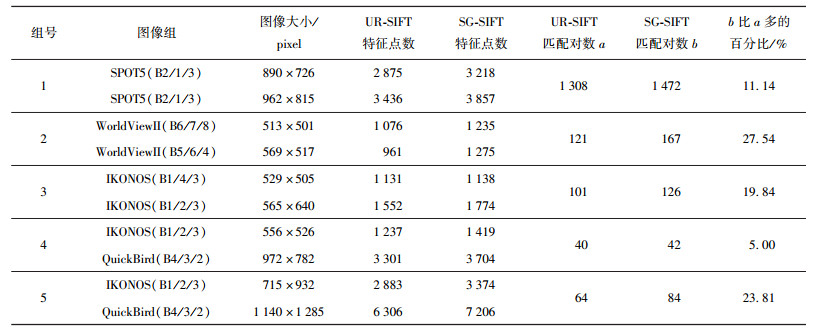
分别用SIFT、UR-SIFT和SG-SIFT处理测试数据,并比较UR-SIFT和SG-SIFT得到的匹配点对数目,其结果如表 1所示.由表 1可知,在待提取特征点数量一定的情况下,SG-SIFT实际提取的特征点数量比UR-SIFT多,且匹配对数也比UR-SIFT平均多17.47%.由3.1节可知,SG-SIFT从DoG尺度空间中提取的特征点数量比值更接近SIFT提取的初始关键点数量比值,缺点的情况少,因而提取的特征点数量较多,最后得到的匹配对数也较多.
|
|
表 1 SG-SIFT与UR-SIFT提取特征点的对比情况 |
从表 1的每组数据中手动选取15组正确匹配点对作为测试数据,分别求取3种方法的RRMSE作为配准准确与否的标准,其对比如图 3所示. SG-SIFT算法比SIFT算法和UR-SIFT算法得到的RRMSE低,说明配准的结果更准确. SG-SIFT剔除了虚假匹配点对,所以RRMSE比SIFT的低;而SG-SIFT比UR-SIFT得到的匹配点对多,得到的转换模型更接近真实.
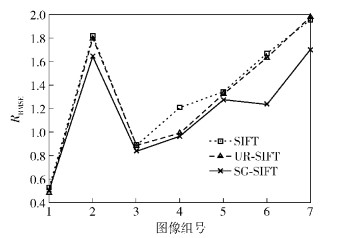
|
图 3 SIFT、UR-SIFT和SG-SIFT的RRMSE对比曲线 |
图 4所示为SG-SIFT算法对表 1中第4组测试数据进行匹配的结果,图中的圆白点表示匹配点. 图 4左侧是QuickBird多光谱影像(B/4/3/2) 得到的匹配点,图 4右侧是IKONOS多光谱影像(B1/2/3) 得到的匹配点. 图 4中的2幅图像是不同传感器获得的图像,其对应的区域Ⅰ和Ⅱ也可清晰地展现2幅图像的匹配点是对应的;图 4中其他匹配对也是对应的. 图 5所示为图 4中图像配准后的镶嵌结果.以上实验表明,SG-SIFT算法可用于同源和多源光学遥感影像的配准,不仅特征点数量少分布均匀,且配准结果更准确.

|
图 4 QuickBird影像与IKONOS影像的匹配结果 |

|
图 5 图 4中图像配准后的镶嵌结果 |
针对光学遥感影像配准提出了SG-SIFT算法,将信号理论中频谱和网格化应用到SIFT算法中,弥补了SIFT算法提取的特征点分布不均匀和UR-SIFT算法在实际提取时常有缺点的不足.实验表明,SG-SIFT算法能有效提取出足够多的特征点以完成光学遥感图像(同源和多源图像)的配准,且提取的特征点在DoG尺度空间和图像空间都分布合理,尺度空间上分布合理保证了该算法的尺度不变性,空间分布合理则保证了图像局部形变时模型求解的精确性;另外,由于该算法需要提前设定特征点数量,故可以控制特征点的数量,尤其对高分辨率图像,降低了后续特征描述子生成和特征匹配过程的计算量,同时有效剔除了虚假匹配点对,使得变换模型求解更准确,提高了配准精度.
| [1] | Zitova Barbara, Flusser Jan. Image registration methods: a survey[J].Image and Vision Computing, 2003, 21(11): 977–1000. doi: 10.1016/S0262-8856(03)00137-9 |
| [2] |
余先川, 吕中华, 胡丹. 遥感图像配准技术综述[J]. 光学精密工程, 2013, 21(11): 2960–2972.
Yu Xianchuan, Lü Zhonghua, Hu Dan. Review of remote sensing image registration techniques[J].Optics and Precision Engineering, 2013, 21(11): 2960–2972. |
| [3] | Lowe David. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision, 2004, 60(2): 91–110. doi: 10.1023/B:VISI.0000029664.99615.94 |
| [4] | Amin Sedaghat, Mehdi Mokhtarzade, Hamid Ebadi. Uniform robust scale-invariant feature matching for optical remote sensing images[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4516–4527. doi: 10.1109/TGRS.2011.2144607 |
| [5] | Yu Le, Zhang Dengrong, Holden Eun-Jung. A fast and fully automatic registration approach based on point features for multi-source remote-sensing images[J].Computers and Geosciences, 2008, 34: 838–848. doi: 10.1016/j.cageo.2007.10.005 |