通过对损耗陷门函数的分析得知, 在关于陷门的任意计算不可求逆的函数提前泄露的情况下, 已有损耗陷门函数的可证明安全性将会受到较大的影响.如何保证损耗陷门函数在此应用场景下仍然是可证明安全的, 是一个有意义的研究问题.为此, 首先使用d线性假设, 构造了一个新的损耗陷门函数, 并利用扩展版的Goldreich-Levin定理, 证明其是辅助输入安全的; 其次通过对Peikert所构造的利用错误学习问题假设的损耗陷门函数进行适当的修改, 也能证明其是辅助输入安全的; 最后从效率和安全性角度出发, 对2个损耗陷门函数进行了分析.
Analyzing the primitive of lossy trapdoor function, we know that all existing lossy trapdoor functions might not be provably secure when the adversary previously gets the related information on the trapdoor. This article presented a new lossy trapdoor function based on the d-linear assumption, and proved it to be auxiliary-input secure by using an extended version of the Goldreich-Levin theorem. It is verified that the slight variance of Peikert's learning with errors based lossy trapdoor function is auxiliary-input secure. Both lossy trapdoor functions in efficiency and security was analyzed.
由于存在广泛的密码学应用[1],损耗陷门函数自提出以来就受到密码学研究者的广泛关注.目前,关于损耗陷门函数构造的研究已有诸多进展[1-5].通过对已有损耗陷门函数进行分析得知,在特定的应用环境中,损耗陷门函数的陷门相关信息可能会提前泄露给攻击者,即攻击者可能会得到陷门sk的一个多项式时间内可计算但难以求逆的函数h(sk).因此,需要考虑在函数h是亚指数困难求逆的情况下,如何保证损耗陷门函数仍然是可证明安全的.
为此,引入辅助输入安全的概念和技术[6-8]作为解决问题的工具.具体而言,利用传统的d线性假设和抗量子计算攻击的错误学习问题(LWE, learning with errors)假设,分别构造了一个新的损耗陷门函数,并证明其是辅助输入安全的.最后从效率和安全性角度出发,对2个损耗陷门函数进行分析.
1 预备知识和基本概念对于损耗陷门函数的定义,可以参考文献[1, 3],在此不再详述.
对于指数困难求逆的定义,可以参考文献[6, 9],在此不再详述.
引理1[8-9] q元数域Fq上的Goldreich-Levin定理.令q是一个素数,f:{0, 1}n→{0, 1}*是任意函数.如果存在一个运行时间为z的区分算法D,使得
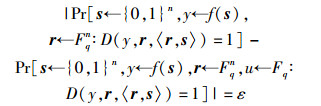
|
则存在一个运行时间为z′=z×poly(n, 2n, 1/ε)的求逆算法A,使得
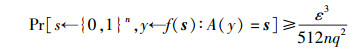
|
由此可知,若函数f:{0, 1}n→{0, 1}*是亚指数困难求逆的,则
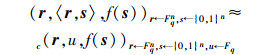
|
对于矩阵形式的d线性假设的定义,可以参考文献[3, 9],在此不再详述.
对于矩阵形式的LWE假设的定义,可以参考文献[10],在此不再详述.进一步,可以将该判定型LWE问题表示为DLWEn, q, β.
2 利用d线性假设的损耗陷门函数2.1 损耗陷门函数的构造令q是一个素数,Fq表示q元域,G表示包含有q个元素的乘法群.对于任意一个g∈G,行向量xT=(x1, …, xn)∈Fqn,用gxT表示行向量(gx1, …, gxn)∈Gn.对于矩阵M=(aij)∈Fqn×m,用gM表示矩阵(gaij)∈Gn×m.给定矩阵M=(aij)∈Fqn×m和行向量gT=(g1, …, gn)∈Gn,定义运算(gT)M为
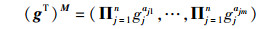
|
类似地,给定矩阵S=(gij)∈Gn×m和行向量xT=(x1, …, xn)∈Fqn,定义运算(S)xT为
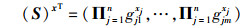
|
由以上定义和运算可得
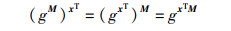
|
对于任意实数ε∈(0, 1),利用d线性假设的辅助输入安全损耗陷门函数族H1由算法(Cinj, Clossy, Vltdf, Vltdf-1)描述如下.
1) 选取一个单射函数:在输入安全参数d的情况下,算法Cinj随机选取一个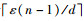
2) 选取一个损耗函数:在输入安全参数d的情况下,算法Clossy随机选取一个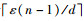
3) 正向计算:给定函数索引σ=(S1, S2)和行向量xT=(x1, …, xn)∈{0, 1}n,算法Vltdf计算函数Vltdf(S1, S2, x)=((S1)xT, (S2)xT)=(t1T, t2T)∈Gd+n.
4) 对于单射函数求逆:给定陷门τ=(g, S)和向量(t1T, t2T),定义Vltdf-1(τ, t1T, t2T)如下.
① (t1T)S=(a1, …, an)∈Gn,t2T=(b1, …, bn)∈Gn;
② hT=(h1, …, hn)=(b1/a1, …, bn/an)∈Gn;
③ 输出xT=(x1, …, xn)=(logg(h1), …, logg(hn)).
2.2 正确性和安全性引理2 若多项式时间内可计算的函数f:{0, 1}d×w→{0, 1}*是亚指数困难求逆的,则对于任意素数q元数域Fq, 正整数n, w>d,A←Fqn×d,S=(s1, …, sw)←{0, 1}d×w,从数域Fq中选取n×w维的秩为d的随机矩阵,即U←Rkd(Fqn×d),满足
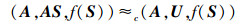
|
其中对于i∈{1, …, w},由f(S)求出任意一个si都是亚指数困难的.
利用混合论证的方法和引理1,可以完成对引理2的证明,在此不再详述.
在引理2中,由于矩阵A和S都是秩为d的满秩矩阵,所以矩阵AS的秩也是d,从而矩阵U的秩也是d.若将AS替换为AS+E,其中E是满秩矩阵,则与之相对应的均匀矩阵U的秩应该是n.事实上,可以将引理2看成引理1的进一步扩展.
定理1 在ε(n-1)>d的情况下,如果q阶循环群G上的d线性假设成立,则函数族H1是一个(n, (n-1)(1-ε))的辅助输入安全的损耗陷门函数族.
证明 首先证明在单射函数情况下,求逆算法的正确性.
此时,单射函数的索引为σ=(S1, S2)=(gA, gAS+E),函数输出为
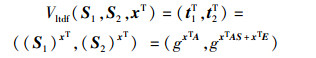
|
而(t1T)S=(gxTA)S=gxTAS.若(t1T)S=(a1, …, an),t2T=(b1, …, bn),则对于任意i∈{1, …, n},bi/ai=gxi.因此,利用陷门S,可以对单射函数正确求逆.
其次证明在损耗函数的情况下,函数是损耗的.
此时,损耗函数的索引为σ=(S1, S2)=(gA, gAS),函数的输出为
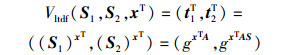
|
按照前面给出的运算规则,gxTA∈Gd是一个d维向量,且AS∈Rkd(Gn×n).因此,单射函数的值域中至多包含2qd个元素.进一步,ε(n-1)>d,因此2n>2qd.所以损耗分支是损耗的,且损耗量是(n-1)(1-ε).
最后证明即使攻击者在得到陷门的亚指数困难求逆的相关信息的情况下,以上损耗函数族和单射函数族仍然是计算不可区分的.需要证明对于任意亚指数困难求逆的函数f,满足
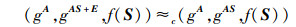
|
(1) |
由引理2可知,(A, AS, f(S))≈c(A, U, f(S))成立,其中U∈Rkd(Fn×n).所以
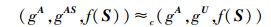
|
(2) |
由于矩阵E是n×n的单位矩阵,可以得到
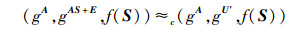
|
(3) |
其中U′←Rkn(Fqn×n).事实上,式(2) 和式(3) 的计算不可区分困难性是等价的.即如果存在一个能以不可忽略的优势成功区分式(2)(或式(3))的算法,则可以很容易地构造一个能成功区分式(3)(或式(2))的新算法.由此可知,在式(2) 成立的情况下,式(3) 的成立是合理的.进一步,由于U、U′与f(S)是相互独立的,且循环群G上的d线性假设成立,可知
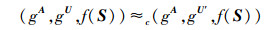
|
(4) |
显然成立.所以,由式(2)~式(4) 可知,式(1) 显然成立.
综上所述,函数族H1是一个(n, (n-1)(1-ε))的辅助输入安全的损耗陷门函数族.
3 利用LWE假设的损耗陷门函数3.1 损耗陷门函数的构造由Peikert[1]所构造的利用LWE假设的损耗陷门函数的一个简单变形也是辅助输入安全的.与原始的Peikert损耗陷门函数相比,该变形构造的主要区别在于模数q是关于安全参数的一个拟多项式,单射函数所对应的陷门是一个分量从{0, 1}中选取的矩阵,差错参数是安全参数的多项式分之一等.下面给出该变形构造的详细描述.
对于任意2的幂次方形式的模数p,正整数n和w,满足n=wlbp,令I是整数上w×w的单位矩阵,行向量pT=(20, 21, …, 2(lbp)-1)∈ 

定义从



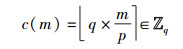
|
其中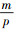



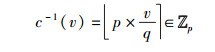
|
其中

利用LWE假设的辅助输入安全的损耗陷门函数族H2由算法(Cinj, Clossy, Vltdf, Vltdf-1)描述如下.
1) 选取一个单射函数:在输入安全参数d的情况下,选取正整数n和w,差错因子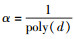



2) 选取一个损耗函数:在输入安全参数d的情况下,选取正整数n和w,差错因子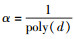



3) 正向计算:给定函数索引σ=(A, B)和行向量xT=(x1, …, xn)∈{0, 1}n,算法Vltdf计算函数Vltdf(A, B, xT)=(xTA, xTB)=(t1T, t2T)∈
4) 对于单射函数求逆:给定陷门τ=S和向量(t1T, t2T),定义Vltdf-1(τ, t1T, t2T)如下.
① 计算vT=t2T-t1TST,mT=c-1(vT)∈
② 求解xTG=mT,其中mT为分量在{0, …, p-1}中与mTmodp相等的唯一整数向量;
③ 输出xT=(x1, …, xn)∈{0, 1}n.
3.2 正确性和安全性引理3[7-8] 令β>0,q∈

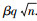
引理4[7-8] 令β>0,q∈

定理2 对于安全参数d∈
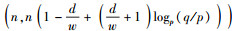
与定理1相类似,利用引理3和引理4可以完成定理2的证明,在此不再详述.
4 效率及相应安全性假设的对比分析本节从效率、损耗量情况和安全性假设等方面出发,对损耗陷门函数族H1和H2进行分析.
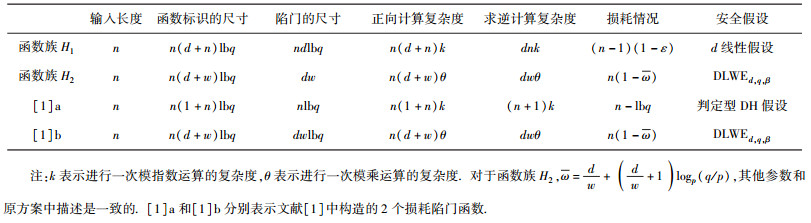
对于利用d线性假设的损耗陷门函数族H1,选取模数q=2O((lbd)t).相应的函数索引需要占用n(d+n)lbq比特的存储空间,单射函数的求逆陷门需要占用ndlbq比特的存储空间.对该函数族进行正向计算需要n(d+n)个模指数运算,利用陷门进行求逆则需要dn个模指数运算,且当输入长度为n的情况下,损耗量为(n-1)(1-ε).
对于利用LWE假设的损耗陷门函数族H2,选取模数q=2O((lbd)t).相应的函数索引需要占用n(d+w)lbq比特的存储空间,单射函数的求逆陷门需要占用dwlbq比特的存储空间.对该函数族进行正向计算需要n(d+w)个模乘运算,利用陷门进行求逆则需要dw个模乘运算,且当输入长度为n的情况下,损耗量为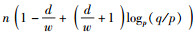
|
|
表 1 2个新型损耗陷门函数族与已有相关结论的参数对比和分析 |
由以上分析可知,2个损耗陷门函数族的存储代价相当,函数族H1的计算代价较高,且损耗量相对较大;函数族H2的计算代价较低,且损耗量相对较小.另外,虽然所构造的2个损耗陷门函数族的效率相对略低,但与已有的损耗陷门函数族相比的优势是能证明是辅助输入安全的.
5 结束语首先,分析在攻击者得到与单射函数的陷门相关的辅助输入信息的情况下,现有损耗陷门函数的可证明安全性会受到较大影响;然后,利用d线性假设和LWE假设,分别构造了一个损耗陷门函数族,并利用扩展版的Goldreich-Levin定理,证明这2个损耗陷门函数是辅助输入安全的;最后,详细地分析这2个损耗陷门函数的效率和安全性,表明这2个损耗陷门函数族相对的优势和不足.此外,文中所用到的概念和技术,可以进一步扩展到all-but-one或all-but-many损耗陷门函数的构造上.
笔者构造的2个损耗陷门函数存在的缺点是存储和计算效率相对略低.如何构造高效的辅助输入安全的损耗陷门函数是进一步的研究方向.
| [1] | Peikert C, Waters B. Lossy trapdoor functions and their applications[C]//Cynthia Dwork (Ed.). Proceedings of STOC 2008. Victoria, British Columbia, Canada: ACM, 2008: 187-196. |
| [2] | Mol P, Yilek S. Chosen-ciphertext security from slightly lossy trapdoor functions[C]//Phong Q Nguyen, David Pointcheval (Eds.). Proceedings of PKC 2010: LNCS 6056. Paris, France: Springer, 2010: 296-377. |
| [3] | Freeman D M, Goldreich O, Kiltz E, et al. More constructions of lossy and correlation-secure trapdoor functions[C]//Phong Q Nguyen, David Pointcheval (Eds.). Proceedings of PKC 2010: LNCS 6056. Paris, France: Springer, 2010: 279-295. |
| [4] | Hofheinz D. All-but-many lossy trapdoor functions[C]//David Pointcheval, Thomas Johansson (Eds.). Proceedings of EUROCRYPT 2012: LNCS 7237. Cambridge, UK: Springer, 2012: 209-227. |
| [5] | Hemenway B, Ostrovsky R. Extended-DDH and lossy trapdoor functions[C]//Marc Fischlin, Johannes Buchmann, Mark Manulis (Eds.). Proceedings of PKC 2012: LNCS 7293. Darmstadt, Germany: Springer, 2012: 627-643. |
| [6] | Dodis Y, Kalai Y T, Lovett S. On cryptography with auxiliary input[C]//Michael Mitzenmacher (Ed.). Proceedings of STOC 2009. Bethesda, MD, USA: ACM, 2009: 621-630. |
| [7] | Dodis Y, Goldwasser S, Kalai Y, et al. Public key encryption schemes with auxiliary inputs[C]//Henri Gilbert (Ed.). Proceedings of EUROCRYPT 2010: LNCS 5978. French Riviera: Springer, 2010: 361-381. |
| [8] | Goldwasser S, Kalai Y, Peikert C, et al. Robustness of the learning with errors assumption[C]//Andrew Chi-Chih Yao (Eds.). Proceedings of ICS 2010. Beijing, China: Tsinghua University, 2010: 230-240. |
| [9] | Brakerski Z, Segev G. Better security for deterministic public encryption: the auxiliary-input setting[C] //Phillip Rogaway (Ed.). Proceedings of CRYPTO 2011: LNCS 7073. Santa Barbara, CA, USA: Springer, 2011: 543-560. |
| [10] | Regev O. On lattices, learning with errors, random linear codes, and cryptography[C]//Harold N Gabow, Ronald Fagin (Eds.). Proceedings of STOC 2005. Baltimore, Maryland, USA: ACM, 2005: 84-93. |