指出了晶体外延生长模式现有理论描述的若干问题, 包括:① 弗兰克-范·德·默夫模式被描述为仅存在于衬底表面能优势度为正值的情形中, 这和晶格失配度足够小的2种材料能够以该模式交替生长的实验事实不符; ② 对于不同的衬底表面能优势度, 弗兰克-范·德·默夫模式与斯特兰斯基-克拉斯塔诺夫(S-K)模式之间的转换被描述为发生在某一固定的晶格失配度上, 这显然是不合理的; ③ 由弗兰克-范·德·默夫模式似可直接转换为沃尔默-韦伯模式, 反之亦然, 这一描述值得质疑.针对这些问题, 提出了改进的、更加完备的理论描述, 其中引入了"准弗兰克-范·德·默夫模式"的概念.在此基础上, 提出了"后S-K异质兼容生长模式"的概念, 并探讨了基于该模式实现高质量异质兼容体材料生长的可能性.
Some problems are found in currently-available theoretical description of epitaxial crystal-growth mods, including that ① Frank-van der Merve mode is described as it only exists for positive dominance-level of the substrate surface energy and this is not in agreement with the experimental fact that a pair of materials with small enough lattice mismatch between them can grow alternately both in the Frank-van der Merve mode; ② the transition between Frank-van der Merve mode and Stranski-Krastanow (S-K) mode is regarded as it happens at a fixed lattice mismatch for different dominance-levels of the substrate surface energy and this description seems obviously unreasonable; ③ the direct transitions from Frank-van der Merve mode to Volmer-Weber mode and vice versa are supposed possible and the truthfulness of this understanding might be seriously suspected. Taking these problems into consideration, a modified and more comprehensive theoretical description is proposed and the concept of quasi-Frank-van der Merve mode is introduced in it. Based upon the new theoretical understanding, the concept of "post S-K compatible-heterogeneous-growth mode" is proposed and the possibility to realize high quality compatible heterogeneous bulk crystal growth based on this new growth mode is investigated.
晶体外延生长是半导体电子学和光电子学乃至整个固体物理学中的一个基本问题.在各种半导体纳异质结构蓬勃兴起和与异质兼容外延生长密切相关的光子/光电集成技术亟待突破的今天,研究这个问题的意义就更加彰显.笔者将在文中就晶体外延生长的模式给出更为完备的理论描述,并在此基础上探讨解决高质量异质兼容体材料生长问题的根本性途径.
1 关于晶体外延生长模式的现有理论描述目前公认的晶体外延生长模式包括弗兰克-范·德·默夫(Frank-van der Merve)模式、斯特兰斯基-克拉斯塔诺夫(Stranski-Krastanow)模式和沃尔默-韦伯(Volmer-Weber)模式3种.这3种模式可分别简称为“F-vdM模式”、“S-K模式”和“V-W模式”[1-3].其中,常规的晶格匹配和准晶格匹配外延层生长采用的都是F-vdM模式,而S-K模式则被广泛地应用于量子点的制备之中.
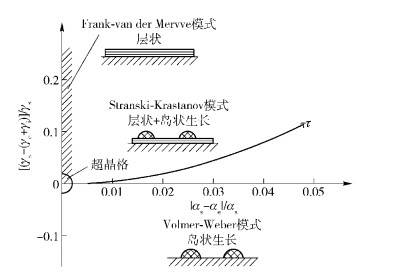
现有理论中所述各种晶体外延生长模式出现的条件如图 1所示[1].图中横轴|as-ae|/as表示衬底材料和外延层材料之间的晶格失配度,其中as和ae分别为衬底材料和外延层材料的晶格常数;纵轴[γs-(γe+γi)]/γs表示衬底材料的表面能γs相对于外延层建构能(γe+γi)(衬底材料的表面能γe与外延层材料和衬底材料之间的界面能γi之和)的优势度,可简称为衬底表面能优势度(注:“外延层建构能”和“衬底表面能优势度”均为笔者建议采用的术语).
|
图 1 现有理论中各种晶体外延生长模式出现的条件 |
由图 1可知,按照现有理论,对应于横轴下方整个区域的晶体外延生长模式皆为V-W模式,其特征为直接成岛生长;而在横轴上方区域中,上述3种模式都可以出现.其中,F-vdM模式出现在纵轴附近沿竖直方向的窄条区域中(图 1中的阴影斜线部分),其特征为层状生长;另外2种模式出现的区域则以一条从原点出发单调上升的特征曲线τ为界,在该曲线上方区域中出现的为S-K模式,其特征为先层状生长(所谓的“浸润层生长”)、后岛状生长,而在该曲线下方区域中出现的则是前已述及的以直接成岛生长为特征的V-W模式.位于横轴上方的V-W模式区域和横轴下方的整个区域连在一起,构成了一个完整的V-W模式区域.
然而不难发现,这样的描述其实是有问题的.譬如,图 1中原点附近有一个被标注为“超晶格”生长区域的半圆形区域.按照图示,该区域的上半部分和下半部分分别对应于F-vdM模式和V-W模式.这显然与事实上的超晶格生长模式相矛盾.超晶格结构中的每一层都是按照F-vdM模式生长的,也就是说,其中没有任何一层是按照直接成岛的V-W模式生长的.更一般地说,图示情形是与晶格失配度足够小的2种材料能够以F-vdM模式交替生长的实验事实不相符的.此外,笔者还在上述描述中发现了若干其他问题.所有这些问题均表明上述描述是不完备的,必须加以修正和补充,这些修正和补充便构成了第2节的内容.
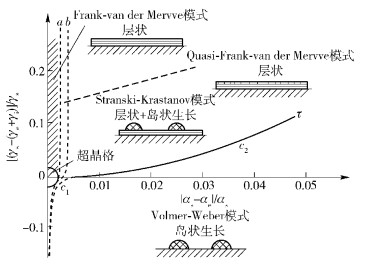
2 晶体外延生长模式的完备描述笔者拟给出的晶体外延生长模式的完备描述如图 2所示.
|
图 2 晶体外延生长模式完备描述示意图 |
相应的修正和补充要点如下:
首先,第1节已经提到半圆形“超晶格”生长区域中不能存在V-W模式.也就是说,横轴上方纵轴附近用阴影斜线标示的窄条状F-vdM模式区域应该延伸至横轴下方,且至少应能覆盖半圆形“超晶格”生长区域的下半部分.那么,这种“延伸”会受到什么限制呢?笔者拟通过下面的讨论来回答这个问题.
当组成超晶格的2种材料确定之后,假定其中每一层的厚度都不至于太小,则相应的3个能量值γs、γe和γi可以被认为是固定不变的.于是可做如下推断:在半圆形“超晶格”生长区域的上半部分,已知[γs-(γe+γi)]/γs>0,此式所对应的情形是在表面能为γs的材料上生长表面能为γe的材料.容易证明,如果是在表面能为γe的材料上生长表面能为γs的材料,则必有[γe-(γs+γi)]/γe < 0.也就是说,当交替生长上述2种材料以形成超晶格的时候,或者更严谨地说,当交替生长上述2种材料以形成各层厚度较大的多层异质结构时,所对应的图 1中的位置是在横轴上下来回变动的.由于在横轴下方的区域中衬底表面能优势度为负值,故实现F-vdM模式要比在横轴上方区域来得困难,或者说2种材料之间的晶格失配度必须取更小的值. F-vdM模式区域越向下方延伸,晶格失配度的取值范围就越小,或者说F-vdM模式发生的位置就越靠近纵轴.故在横轴下方,F-vdM模式区域呈宽度越往下越小的拖尾状.
在讨论过横轴下方的情形后,再看横轴上方的情形,可以顺势得出一个合理的结论:横轴上方的F-vdM模式区域自然也不应该是一个宽度不变的竖直的长条,其宽度应该是越往上越宽的.
综上所述,便可以画出F-vdM模式区域的右边界轮廓线,即曲线a(暂为定性曲线).于是,整个F-vdM模式区域便是处于纵轴和曲线a之间的区域.这是笔者对晶体外延生长模式现有理论描述的第1点修正.
其次,在现有理论描述中,横轴上方纵轴附近用阴影斜线标示的窄条状F-vdM模式区域和半圆形“超晶格”生长区域在横轴上的宽度是相等的.这表明现有理论描述中的F-vdM模式是以外延层足够厚时无位错或无明显位错为特征的.为了讨论方便,且将注意力先集中在横轴上方的区域中.显然,上面给出的曲线a就成为F-vdM模式区域与S-K模式区域的分界线.这里又出现了一个新的问题——随着晶格失配度的加大,生长模式从F-vdM模式区域直接进入S-K模式区域意味着相应的外延生长由无位错或无明显位错的层状生长直接“突变”为浸润层上的岛状生长!这几乎是不可能的!这是因为,在这2种情况之间一定会有、事实上也的确有一个位错不断加大的过渡阶段.当位错加大到某一程度时,量变引起了质变,于是出现了岛状生长.换言之,在F-vdM模式区域与S-K模式区域之间实际上存在着一个过渡性的、以存在明显位错的层状生长为特征的区域,不妨称为“准F-vdM模式”区域.于是,曲线a(且仅注意它在横轴上方的部分)便变成了F-vdM模式区域与准F-vdM模式区域的分界线.与曲线a的得出类似,自然还可以定性地画出一条作为准F-vdM模式区域与S-K模式区域分界线的曲线来,这便是曲线b(同前,仅注意它在横轴上方的部分).这是笔者对晶体外延生长模式现有理论描述的第2点修正.此处尚未涉及对现有理论表述中曲线τ的修正,相关内容将在下面讨论.
再次,在图 1所示的现有理论描述中,在F-vdM模式区域右边界与曲线τ的交点处(该点尽管已经很接近横轴,但严格地讲仍高于横轴)及该交点至横轴的垂直连线上,其左边的F-vdM模式可以直接转换为其右边的V-W模式,反之亦然,这一描述值得质疑.为了得出合理的描述,且将注意力转向横轴下方的区域.合乎逻辑的推断(见图 2)是:正如F-vdM模式区域会延伸至横轴下方一样,准F-vdM模式区域和S-K模式区域也都应该延伸至横轴下方.这是因为,在横轴下方,随着晶格失配度的加大,不经过准F-vdM模式区域和S-K模式区域,而由F-vdM模式区域直接进入V-W模式区域同样是不可能的.这样一来,实际上揭示了一种新的可能性,即在横轴下方的特定区域中,也可以像在横轴上方区域中那样,借助于S-K模式生长量子点了!不过,尽管如此,横轴下方的情形和横轴上方的情形还是有很大区别的.正如曲线a(F-vdM模式区域的右边界)在横轴下方是迅速向纵轴靠拢的,曲线b(准F-vdM模式区域与S-K模式区域的分界线)在从横轴上方延伸至横轴下方时也会迅速向曲线a靠拢;同时,现有理论描述中横轴上方的曲线τ也必须加以修正,特别是其靠近纵轴的部分必须做较大修正.由于曲线τ也应延伸至横轴下方,故它不能随着晶格失配度的减小而抵达原点,而必须在晶格匹配度减小至某一值时转而迅速地向下延伸,继之向曲线b靠拢.统观横轴上下,这条新的曲线(准S-K模式区域与V-W模式区域的分界线)可以分作2段,第1段记作c1,第2段记作c2. c1与原来的曲线τ差别很大,c2则与原来曲线τ上的相应部分非常接近,甚至可以认为是重合的.
此外,类似于前面已提出的“准F-vdM模式”,在S-K模式和V-W模式之间也有可能存在一个过渡性的、以存在明显位错的“层状+岛状”生长为特征的“准S-K模式”.但目前尚无证据表明一定存在该模式,故在图 2中未予标示.这一问题有待今后进一步研究.
至此,笔者就晶体外延生长模式给出了一个新的、更为完备的理论描述.
3 基于“后S-K异质兼容生长模式”实现高质量异质兼容体材料生长的可能性异质兼容外延生长是发展大规模、高性能、高性价比光子集成和光电集成技术必须解决的一个基本问题,因而针对特定的材料组合(如InP/GaAs、GaAs/Si等)实现高质量异质兼容外延生长成为许多研究者努力的目标.
显然,如果指定材料组合的晶格失配度足够小,并具有适当的衬底表面能优势度,相应的生长过程应循F-vdM模式.这是一种最完美的异质兼容外延生长的方式.然而,这种方式无法适用于InP/GaAs、GaAs/Si等晶格失配度较大的情况.
于是,人们想出了插入低温缓冲层、插入能阻断位错的超晶格结构等方法来尽可能高质量地实现晶格失配度较大情况下的异质兼容外延生长,而且取得了一系列不错的实验结果,但这些方法并非通过某种特定的生长模式从本质上根除位错的产生,而只是在允许位错产生的前提下竭尽弥补之能事而已,因此人们在这条路上走得很艰难.在这里,笔者无意就这些方法做进一步的探究.
本节拟在深入认识各种生长模式及其相互联系的基础上,找到某种基于特定生长模式的、从本质上根除位错产生的方法.显然,以位错伴生为特征的准F-vdM模式和以低质量岛状生长为特征的V-W模式都不是笔者所需要的模式.于是,笔者的注意力自然集中到了最后一种可供选择的模式上,即以较大晶格失配度和无位错岛状生长为特征的S-K模式.
乍看上去,鉴于其岛状生长的特征,S-K模式好像也不是笔者所需要的模式.然而,细考可知,S-K模式有其独到的优势,不宜对它做简单的否定.
近年来,笔者和同事们致力于将纳米线、量子点等纳异质结构的自组织生长与高质量的异质兼容体材料生长结合起来,所做尝试包括在异质兼容外延生长过程中引入纳米线或量子点结构以提高生长质量.在实验中,有迹象表明,引入基于S-K模式生长出来的量子点结构较之引入其他结构对于提高生长质量具有更为明显的效果.这一迹象促使笔者对S-K模式产生了更大的研究兴趣.
S-K模式本身的特殊性在于它是“物极必反”、“否极泰来”规律的产物.具体而言,该模式的无位错生长特征居然是准F-vdM模式下位错不断积累以至于层状生长不得不因“危机爆发”而“崩溃”式地转变为以浸润层为铺垫的岛状生长的自然产物.从无位错的F-vdM模式到有位错的准F-vdM模式,再到无位错的S-K模式是一个典型的“否定之否定”过程,最终提供了在某一种晶体材料上无位错地生长另一种晶格大失配的晶体材料的可能性.诚然,S-K模式下的外延生长不再是通常进行体材料生长时所要求的层状生长,但其无可替代的优点则是无位错生长.如果能在按照S-K模式生长出高质量的量子点之后,顺势而为,以某种特殊方式继续进行特别指定的第3种材料的无位错生长(其晶格常数介于S-K模式生长情形中衬底材料和外延材料两者的晶格常数之间),并使之转化为层状生长,就有可能扬S-K模式之无位错之长,避S-K模式之非层状生长之短,从而实现以上述第3种材料为目标外延层的大失配体材料异质兼容外延生长.笔者将这种生长方式叫作“后S-K异质兼容生长模式”.以往人们对于S-K模式的研究兴趣往往在于且止于量子点及相关量子点器件的制备,故鲜有人对这种“后S-K”模式进行研究.而今笔者提出这一模式既属久思之“偶得”,也属异质兼容外延生长技术自身发展之必然.
通常,为了制备量子点器件,人们在依S-K模式制得量子点结构之后需要在该结构上通过进一步的外延生长覆盖一定厚度的与衬底相同的材料.就器件制备而言,这一步骤形成了器件物理所要求的双异质结构,并将后续工艺中的材料体系大体上(存在一定程度的残余应变)恢复为与衬底相同的材料体系;就外延生长过程本身而论,这一步骤使得量子点结构中的应变分布趋于稳定.同时,也正是基于与这一步骤相关的现象和机理,“后S-K异质兼容生长模式”的思想得以形成.
首先,需要假定该结构中的量子点密度足够高(譬如达到1010~1011量级)且相应的位错密度可忽略.一般而言,在量子点结构上生长衬底材料覆盖层时,覆盖层中应变分布的起伏性状将与量子点结构的分布情形相对应,在与量子点对应的部分应变会大一些,而在与浸润层相对应的部分应变则会小一些;具体地,在密度足够高的量子点结构上生长上述覆盖层时,相应的应变起伏会呈现出一定程度的“钝化”,因此可以采用平均应变的概念来大体上描述该覆盖层中某一厚度位置上应变的强弱,进而还可以采用平均晶格常数的概念来大体上描述该覆盖层中某一厚度位置上晶格常数的大小.厚度越大,采用上述平均应变和平均晶格常数描述覆盖层性状的准确程度就越高.此外,更为重要的是,随着厚度位置的增高,上述平均应变应该逐渐趋于零,而上述平均晶格常数应该逐渐趋于绝对驰豫的衬底材料的晶格常数.因此,不同的覆盖层厚度值所对应的平均晶格常数必定介于绝对驰豫的量子点材料(或“岛材料”)和绝对驰豫的衬底材料两者的晶格常数之间.其次,再假定想要进行的大失配体材料异质兼容外延生长的目标外延层在绝对驰豫情况下的晶格常数也恰好处于上述区间中.在此情况下,一定能够找到一个合适的覆盖层厚度值,在该厚度上覆盖层的平均晶格常数与目标外延层的晶格常数相同.若在覆盖层的厚度达到该值之时开始在其上外延生长目标外延层,显然应该能顺利地实现无位错的体材料生长,从而达到完美的异质兼容生长的目的.诚然,一般而言,由此形成的目标外延层可能存在的问题是其表面的平整性差和其内部应力分布的不均匀.换言之,以往在异质兼容外延生长中所面对的位错方面的挑战由此转化成了外延层表面形貌和应力分布方面的挑战.笔者相信,后者有可能通过温度、压力、各种材料组分的供给速率等工艺参数的调整以及总体生长程序的优化而得到解决.特别是,当覆盖层和目标外延层的厚度都较大时,这一问题的严重性将会显著降低.
以上讨论尚未涉及特定的材料组合(包括衬底、量子点结构和目标外延层3种材料)关系对于“后S-K异质兼容生长模式”生长的制约.实际上,也许会遇到特定材料组合不能直接满足“后S-K异质兼容生长模式”生长条件的情况.若果真如此,则须选择一种合适的过渡性材料组合,先实现该材料组合的“后S-K异质兼容生长模式”生长,继而以该材料组合中的“过渡目标外延层”作为新的基底继续通过“后S-K异质兼容生长模式”生长终极目标外延层,从而“接力式”地实现所需的高质量异质兼容生长.
4 结束语通过给出晶体外延生长模式的完备理论描述,深化了对于晶体外延生长规律的认识,这些认识有可能推动相关理论和实验研究工作的进展.同时,通过对“后S-K异质兼容生长模式”的探讨,预言了一种实现高质量异质兼容外延生长的新途径,这对于光子集成和光电集成技术的发展或许具有开拓意义.
| [1] | 冯端, 师昌绪, 刘治国. 材料科学导论--融贯的论述[M]. 北京: 化学工业出版社材料科学与工程出版中心, 2002: 41-43. |
| [2] | ж·и·阿尔费罗夫. 科学与社会[M]. 张兰芬, 王丽, 任晓敏, 等译. 北京: 北京邮电大学出版社, 2008: 601-602. |
| [3] | Dubrovskii V G. Nucleation theory and growth of nanostructures, Springer, 2014: 18-24. |


