针对IEEE 802.11系列标准中分布式协调功能(DCF)的缺点,提出了一种简单有效的改进DCF算法.其主要的改进集中在2方面:在经典DCF的基础上,将第0级退避的退避窗口值加倍;使用选择概率p将第0级退避窗口分割成2部分.为了精确地反映改进后协议的性能,建立了二维马尔可夫模型,并将其与经典DCF比较.数值仿真结果表明,改进后的DCF协议在终端节点密度较大时,其吞吐量和时延等性能参数要比经典的DCF优越.
In view of shortcomings of distributed coordination function (DCF) in IEEE 802.11 series standard, a simple but effective improved DCF mechanism was proposed. Main improvements are focuing on the size of backoff window and it's probability was chosen in 0 backoff stage: doubling the backoff window size of 0 backoff stage based on original mechanism and using probability p to divide the window size of 0 backoff stage into two parts. For purpose of reflecting the performance accurately, a comprehensive analytic model was constructed. We compare it with the classical DCF scheme and numerical simulation. It is shown that the new DCF mechanism has better performs than that of classical DCF in the case of dense terminal and heavy offered load.
DCF作为IEEE 802.11系列协议MAC层的最基本接入方式,其采用基于冲突避免的载波监听多址接入(CSMA/CA, carrier sense multiple access with collision detection)机制来实现随机接入.对DCF进行建模分析和改进已经成了当前计算机通信领域的一个研究热点[1-2].
虽然DCF机制已经在IEEE 802.11系列标准中普遍应用,但是很多研究表明,DCF还存在着一些缺点.例如,随着参加信道竞争的终端数或者终端负载的增加,终端所发送的数据包之间会很容易产生碰撞,从而降低系统的吞吐量,增加丢包率[2-4].为此,大量的研究者从不同的角度对DCF机制进行了改进[4-7].
笔者提出一种新的DCF方案,该方案在原始的DCF机制上做了较少的修改,所以较文献[4-6]的几个方案简单.为了验证该方案的有效性,利用二维马尔可夫模型对其进行建模.为了尽量反映真实网络状况下的协议表现,所建模型还同时考虑了节点的非饱和状态、有限重传次数及信道忙时节点的“冻结”状态.
1 一种新的DCF机制经典的DCF采用二进制退避算法来实现随机多址接入.对于一次传输,退避窗口值在[0,Wi-1]的均匀等概率选择,其中Wi为第i级退避的退避窗口值,其依赖于该数据包的重传次数.通常,当i小于等于最大退避级数时,有Wi=2iW0.当信道监听为空闲时,退避计数器减1;当信道为忙状态时,退避计数器“冻结”.如果信道被监听到空闲的时间超过了DIFS(distributed inter-frame spacing),则“激活”退避计数器[3].
虽然DCF机制在很多IEEE 802.11系列协议中被大量采用,但是它还是有一些固有缺点,正如前面所说的,当节点密度较大时,系统的吞吐量和时延等方面的性能较为低下.为了提高协议的性能,笔者在原协议的基础上,做了以下改进.
1) 将第0级退避的退避窗口值加倍,也就是退避窗口值由W0变为2W0;
2) 用概率p将第0级退避分割为2部分.
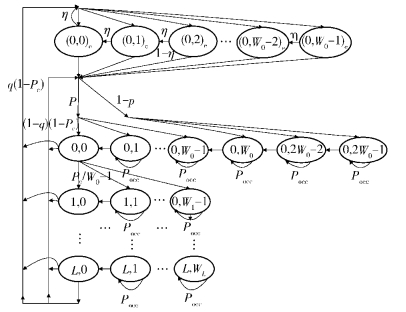
为了方便讨论,用图 1所示的状态转移图来表示改进后的协议.
|
图 1 改进DCF的状态转移图 |
所用到的一些重要数学符号定义如下.
m:最大退避级数;
L:数据包重传次数限制;
K:节点缓冲区数量;
b(i, k):节点在退避状态(i, k)的稳态概率;
b(0, k)e:第i个空状态的稳态概率;
q:在完成发送后,缓冲区为空的概率;
η:没有包到达节点缓冲区的概率;
pc:发送数据包后发生碰撞的概率;
pocc:节点监听到信道忙的概率.
在改进后的DCF机制中,当缓冲区不为空时,节点进入第0级退避,同时以概率p和1-p分别在[0,W0-1]和[W0,2W0-1]范围内均匀选取退避值.
如果在一次成功发送或者碰撞丢包后,节点缓冲区为空,节点设置其空状态退避计数器值(在[0,W0-1]范围内均匀选择)且同时进入空状态.如果在DIFS后,节点缓冲区仍然为空,且空状态退避计数器不为0,此时退避计数器减1;如果退避计数器为0,节点就重新进入空状态.当节点缓冲区有数据包到达时,节点从空状态进入第0级退避.
显然,经典DCF机制和所提改进DCF机制的区别在于第0级退避的处理和空状态的加入,而其他退避过程都采用同样的方式处理.
2 改进DCF机制的建模分析为了方便建模,做以下模型假设.
1) 每个终端节点的包到达率都服从相同参数的泊松分布;
2) 网络中所有终端都具有相同的结构且每个终端都能“听”到其余的所有终端;
3) 每个节点发生数据包碰撞的概率不依赖于该节点的发送历史.
结合图 1所示的状态转移图,可以使用Bianchi模型对改进DCF机制进行建模[2]. Bianchi模型假设节点处于饱和状态,即节点在任何时刻都有数据包需要发送.为了更加完整地分析整个过程,假设缓冲区处于非饱和状态.
由马尔可夫链的归一化条件可知
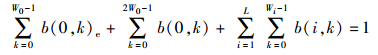
|
(1) |
节点在一个时隙内的发送概率为
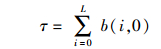
|
(2) |
由于b(i, 0)=pcb(i-1, 0),则有
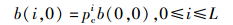
|
(3) |
由式(2) 和式(3) 可得
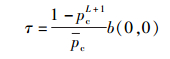
|
(4) |
其中pc=pocc=1-(1-τ)n-1.
结合式(1)、式(3) 和式(4),设x=1-x,则τ可表示为
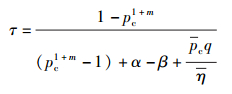
|
(5) |
其中:
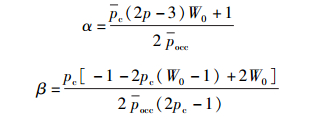
|
由上面的分析可知,τ是关于pc、pocc、m、W0、η、q、p的表达式,如果确定了这些参数,τ的值就可以使用数值方法求得.值得一提的是,如果p=1,所提模型就转化为经典DCF的数学模型.
由于节点数据包的到达服从泊松分布,所以没有数据包到达缓冲区的概率η为
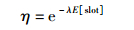
|
(6) |
其中E[slot]为平均时隙长度.由于所有节点共享同一个无线信道,所以有
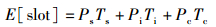
|
(7) |
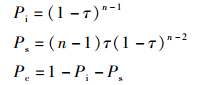
|
(8) |
其中Ps、Pi、Pc分别为信道处于成功发送、空闲、碰撞状态的概率,它们对应的时长分别为Ts、Ti、Tc:

|
(9) |
其中,EIFS表示拓展帧间间隔,SIFS表示最短帧间间隔,ACK表示确认帧的长度.
在基本接入方式下,通常假设Ts=Tc,因此
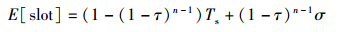
|
(10) |
q为节点一次发送完成后(无论发送成功与否),K个缓冲区为空的概率.由于包的到达为泊松流,所以
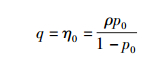
|
(11) |
其中: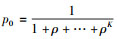
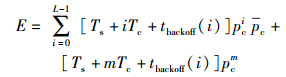
|
(12) |
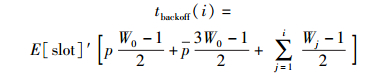
|
(13) |
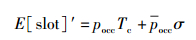
|
(14) |
结合式(5)、式(6) 和式(11),即可求得发送概率τ.
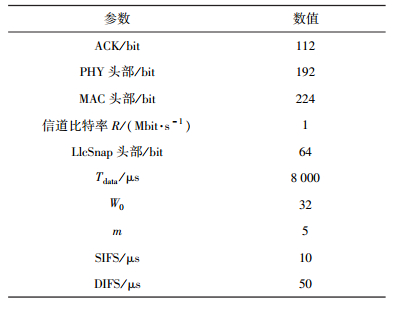
3 仿真分析首先使用数值方法计算出发送概率,进而比较2种DCF协议的性能指标.数值仿真默认参数如表 1所示.吞吐量和节点数关系如图 2所示.
|
|
表 1 数值仿真默认参数 |
|
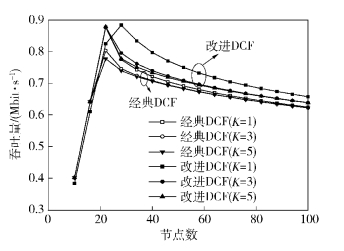
图 2 吞吐量和节点数关系(λ=5,p=0.35,K=1、3、5,Ldata=8000) |
由图 2可知,当节点数较小时,2种DCF方案的吞吐量几乎相等(此时系统处于非饱和状态),但是随着负载或节点数的增加,改进DCF在吞吐量上有一定的优势.例如,当K=1,节点数分别为40、70和100时,改进DCF的吞吐量分别要比经典DCF机制要高10.55%、6.71%和5.28%.
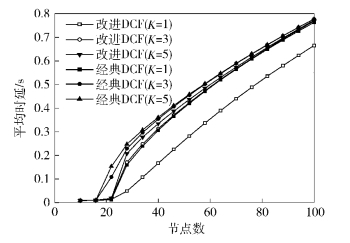
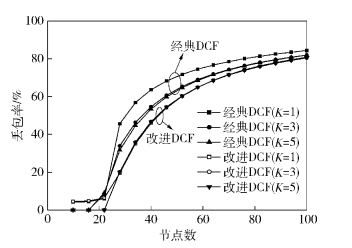
图 3和图 4分别给出了平均时延、丢包率和节点数的关系.可以看出,当节点数目较小时,2种DCF机制的平均时延和丢包率都接近于0,如果节点数继续增加,二者的平均时延和丢包率都呈现大幅增加.但是,改进DCF机制的平均时延要比经典DCF低.例如,当K=1,节点数为50时,改进DCF机制的时延相对于经典DCF减少了0.15 s.
|
图 3 平均时延和节点数关系(λ=5,p=0.35,K=1、3、5,Ldata=8 000) |
|
图 4 丢包率和节点数关系(λ=5,p=0.35,K=1、3、5,Ldata=8 000) |
由数值仿真结果及其分析可以看出,改进后的DCF机制在吞吐量、时延等方面要比未改进前有优势.
4 结束语为了提高IEEE 802.11系列协议中DCF的性能,对经典DCF机制进行了改进,通过建立马尔可夫数学模型对协议进行建模描述,并利用所建立的数学模型进行了数值仿真,比较了改进后DCF和经典DCF机制的吞吐量和时延等重要性能指标.仿真结果表明,改进后的DCF机制在大多数情况下,要比未改进前更有优势.所以,当节点数或负载较大时,改进后的DCF更具适用性,在一定程度上克服了DCF机制的固有缺点.
| [1] |
高峰, 高泽华, 文柳, 等. IEEE 802. 11 a DCF协议吞吐量与时延性能分析[J]. 北京邮电大学学报, 2010, 33(6): 43–47.
Gao Feng, Gao Zehua, Wen Liu, et al. Delay and throughput analysis of IEEE 802.11a based DCF[J].Journal of Beijing University of Posts and Telecommunications, 2010, 33(6): 43–47. |
| [2] | Bianchi G. Performance analysis of the IEEE 802.11 distributed coordination function[J].Selected Areas in Communications, IEEE Journal on, 2000, 18(3): 535–547. doi: 10.1109/49.840210 |
| [3] |
吴大鹏, 王汝言, 武穆清, 等. IEEE 802.11无线网络中DCF模式媒介服务状态分析[J]. 北京邮电大学学报, 2011, 34(4): 101–104.
Wu Dapeng, Wang Ruyan, Wu Muqing, et al. Service status of DCF model in IEEE 802.11 wireless network[J].Journal of Beijing University of Posts and Telecommunications, 2011, 34(4): 101–104. |
| [4] | Feng Zhengyong, Wen Guangjun. Optimal contention window adjustment for asymmetry traffic in erroneous channels over IEEE 802.11 WLANs[J].IEICE Transactions on Communications, 2013, 96(5): 1149–1157. |
| [5] | Simo Reigadas J, Martinez Fernandez A, Ramos Lopez J, et al. Modeling and optimizing IEEE 802.11 DCF for long-distance links[J].Mobile Computing, IEEE Transactions on, 2010, 9(6): 881–896. doi: 10.1109/TMC.2010.27 |
| [6] | Tian Weizhen, Guo Mingrui, Li Zhixin. An improved collision avoidance method for IEEE 802.11 DCF with information-sharing-list[C]//Proceedings of the 2012 International Conference on Information Technology and Software Engineering. Lecture Notes in Electrical Engineering. Berlin Heidelberg, Springer press, 2013: 567-575. |
| [7] | Xu Changchun, Liu Kezhong, Liu Gan, et al. Accurate queuing analysis of IEEE 802. 11 MAC layer[C]//Global Telecommunications Conference, 2008. IEEE GLOBECOM 2008. New Orleans, LO: IEEE press, 2008: 1-5. |