引用本文
万武南, 杨威, 陈运. 一种新的3容错扩展RAID码[J]. 北京邮电大学学报, 2014, 37(5): 75-79.  
WAN Wu-nan, YANG Wei, CHEN Yun. A Toleration Based Extended RAID Code Triple Failures[J]. JOURNAL OF BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS, 2014, 37(5): 75-79.  
Permissions
Copyright©2014, 《北京邮电大学学报》编辑部
《北京邮电大学学报》编辑部 所有
一种新的3容错扩展RAID码
万武南1,2, 杨威1, 陈运2    
1. 成都信息工程学院 信息安全工程学院，成都 610225;
2. 成都信息工程学院 应用密码学研究所，成都 610225
作者简介: 万武南(1978—)，女，副教授，博士，E-mail: nan_wwn@cuit.edu.cn.
收稿日期: 2014-01-21
基金项目: 国家自然科学基金项目(60873216)；四川省教育厅重点项目(12ZA223)
摘要

随着存储系统规模的扩大，如何提高存储系统可靠性成为一个必须解决的问题.目前的双容错独立冗余磁盘阵列(RAID)码已经无法满足存储系统可靠性要求.在双容错行对角奇偶校验(RDP)码的基础上，提出了一种编码冗余率和纠错能力达到编码最优的新的扩展RDP-RAID码，可以允许任意3磁盘同时故障，并给出了一种基于二元矩阵变换的简单和直观的译码算法.与STAT码和EEOD码相比，扩展RDP-RAID码的编译码复杂度、更新复杂度、存储效率的综合性能可达到最优，存储可靠性高.

关键词: 独立冗余磁盘阵列编码     阵列码     行对角奇偶校验码     纠删码    
中图分类号:TN911.22 文献标志码:A 文章编号:1007-5321(2014)05-0075-05 DOI:10.13190/j.jbupt.2014.05.016
A Toleration Based Extended RAID Code Triple Failures
WAN Wu-nan1,2, YANG Wei1, CHEN Yun2    
1. College of Information Security Engineering, Chengdu University of Information Technology, Chengdu 610225, China;
2. Institute of Applied Cryptography, Chengdu University of Information Technology, Chengdu 610225, China
Abstract

As the storage system grows, how to improve the system reliability has become a key issue to the storage system. The redundant array of independent disk (RAID) codes of tolerating double failures can not meet the requirement of reliability in storage system. On the basis of the row diagonal parity (RDP) code for double toleration failures, a new class of extended RDP-RAID code for triple storage failures was presented. The three nodes failure recovery capability for a given data redundancy were optimal. The simple and intuitive algorithms of encoding and decoding were proposed by using binary matrix transformation. Analysis shows that the comprehensive properties of the proposed code are better than the STAT code and the EEOD code, such as update complexity, encoding and decoding complexity, storage efficiency. And it shows high reliability for storage systems.

Key words: redundant array of independent disk code     array code     row diagonal parity code     erasure code    

在RAID存储系统中，磁盘的容错能力来自于底层所采用的RAID编码，因此RAID编码的性能很大程度上决定了RAID的整体性能.衡量RAID码最重要的参数分别为码的编译码计算复杂度、存储效率以及码的更新复杂度[1-2].为了使Singleton界、冗余率和纠删能力达到最优，具有(MDS，maximum distance separable)性质的多种RAID码被提出，如EVENODD码[3]、C码[4]、RDP码[5]、H码[6]等，允许任意2磁盘出错，编译码过程只需要异或运算.为了提高RAID码容错能力，研究者对现有双容错阵列码基础进行了扩展，提出STAR码[7]、EEOD码[8]和Like-RS码[9]，这3种码都是在EVENODD码的基础上进行扩展，允许3磁盘同时故障，并且继承了EVENODD码特性，即冗余校验位计算不均衡，容易造成I/O瓶颈.

笔者在RDP码的基础上，提出了一种扩展RDP-RAID码，保留了RDP码更新复杂度均衡的性能，并提出二元矩阵的简单译码算法.与STAR码和EEOD码相比，扩展RDP-RAID编译码计算复杂度、存储效率以及码的更新复杂度性能更优，缓解了RAID的I/O瓶颈问题，并能为存储系统提供更高可靠性.

1 扩展RDP-RAID码编码方法1.1 扩展RDP-RAID编码

RDP码是由Peter Corbett等提出的一种具有MDS性质的双容错RAID码，与EVENODD码相比，RDP码具有更优的编译码复杂度和磁盘小写性能[5].为了提高RAID容错能力，允许3个磁盘同时故障，对RDP码进行扩展，增加1列校验列.扩展的RDP码放在(m-1)×(m+2) 阶二维阵列中，其中前m-1列为源数据列，后3列为校验列，其编码计算公式如式(1)~式(3) 所示.

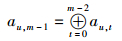
(1)
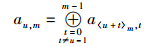
(2)
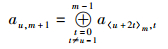
(3)

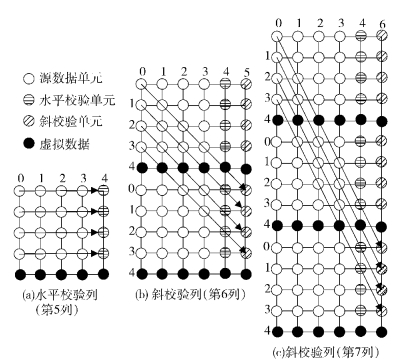
其中：0≤u≤m-2，m为素数；ai, j为第j列第i行的源数据位或校验位；〈x〉m表示x模m.扩展RDP-RAID码编码结构如图 1所示，横坐标表示列数，纵坐标表示分块数据.

图 1 扩展RDP-RAID码编码结构
1.2 扩展RDP-RAID码代数编码方法

扩展RDP-RAID码的编码过程也可用GF(2) 域上的矩阵来描述，下面给出相关定义[8].

定义1  在GF(2) 有限域上，定义一个矩阵集{Im, Em, Em2, …, Emm-1}，其中Emα为一个m×m矩阵，集合中矩阵Emα=(ei, j)m×m定义为

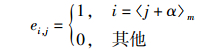
(4)

其中：Emm=Im，Em-1=Emm-1，Em-α=Emm-α，Im为m×m的单位矩阵.

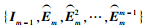
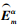
定义2  在有限域GF(2) 上，定义一个矩阵集，其中为由Emα删除最后一列和最后一行构造的(m-1)×(m-1) 矩阵.

若扩展RDP-RAID码的二维阵列每列数据可记为ci=[a0, i, a1, i, …, am-2, i]T，0≤i≤m+1，根据扩展RDP-RAID码的编码公式(式(1)~(3))，编码代数构造公式为

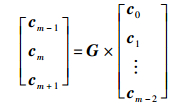
(5)

其中G为码的生成矩阵，定义为

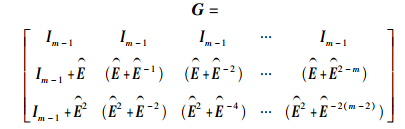
(6)
2 扩展RDP-RAID码译码算法

在RAID结构中，是预先知道数据失效所在磁盘位置的.若失效数据列数小于3，则直接采用类似RDP码译码算法.若3列数据失效，扩展RDP-RAID码并不能直接采用RDP码的Zig-Zag译码算法，则采用GF(2) 域上码的生成矩阵变换的译码算法.

假设3列失效源数据的列号分别为u1、u2、u3 (0≤u1＜u2＜u3≤m-2)，根据式(1)~式(3)，可预先计算出3组校验算子S(0)、S(-1)、S(-2)，其计算公式分别为

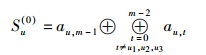
(7)
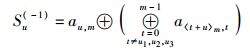
(8)
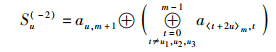
(9)

其中0≤u≤m-2，则

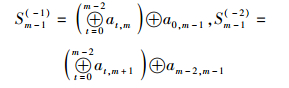
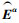
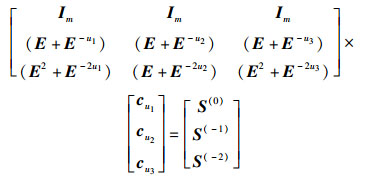
此时扩展码中的二元矩阵可用Emα替换，则式(7)~式(9) 可写为

(10)

接下来的译码则可以通过二元矩阵变换恢复失效3列数据.

1) 式(10) 左右两边依次左乘矩阵：

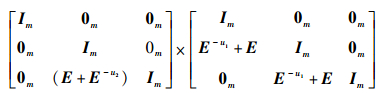
则可以变换为

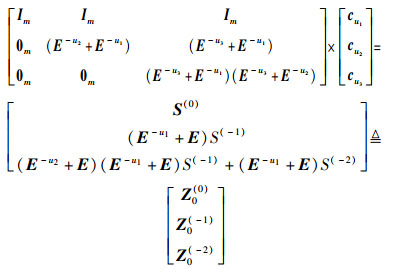
(11)

2) 式(11) 左右两边再左乘矩阵：

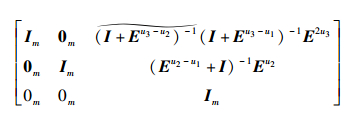
根据文献[8]，公式(11) 可转换为

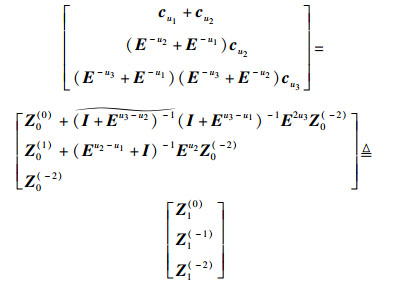
(12)

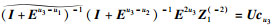
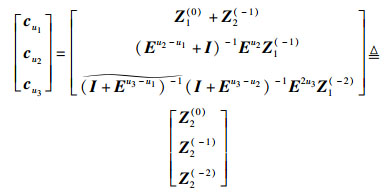
因为Z1(-2)=(E-u3+E-u1)(E-u3+E-u2)cu3，所以.又因为最后一行数据位为零，所以Ucu3=cu3.依次转换，最后3列失效源数据cu3、cu2、cu1恢复为

(13)

经过式(10)~式(13) 变换，依次恢复cu3、cu2、cu1 3列失效数据，译码结束.

3 扩展RDP-RAID码性能分析

存储效率、编译码计算复杂度、更新复杂度是衡量一类RAID编码的重要指标.为了分析RAID码的性能，假定每个数据位为1 bit.

3.1 存储效率

存储效率是指RAID码中源数据位所占总数据位的比例.扩展RDP-RAID码中数据位占m-1列，3列为冗余数据列，其存储效率为(m-1)/(m+2)，根据编码理论中Singleton bound定理[3]可知，存储效率和冗余能力达到了3容错RAID码最优.

3.2 编译码计算复杂度

编译码计算复杂度正比于在编译码过程中所需异或计算的次数.扩展RDP-RAID码编码异或次数由式(1)~式(3) 计算而得为3(m-2)(m-1)，而扩展RAID-RDP码源数据位为(m-1)(m-1) 位，因此编码效率为3-1/m，而EEOD码和STAR码的编码效率为3-1/(m-1)[7-8]，扩展码编码效率达到3容错最优值.

扩展RDP-RAID码译码过程相对于编码过程要复杂，需计算每比特所需要的译码异或次数.根据第2节译码过程，可分析计算校验算子S(0)、S(-1)、S(-2)需要总异或次数为(3m-8)(m-1)-2，而矩阵的变换计算需要9(m+1) 次，则总共需要(3m+1)(m-1)+16次异或运算.而STAR码译码总的异或次数为(3m+2ld+lh)(m-1)-3[7]，EEOD码译码异或次数为(4ld-2+3m)(m-1)-3[8].

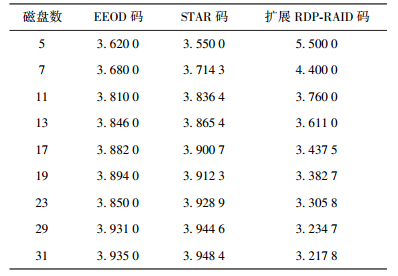
3种纠删码译码效率比较如表 1所示.随着磁盘数的增大，扩展RDP-RAID码的译码复杂度呈现逐渐降低趋势，接近3容错译码最优值3；而EEOD码和STAR码译码复杂度逐渐增大，接近4.在磁盘数大于7时，扩展RDP-RAID码的译码复杂度要低于EEOD码和STAR码.

表 1 3种纠删码每比特译码所需异或次数
3.3 更新复杂度

更新复杂度是指每更新一个数据块所需要同时更新另外数据块的个数.

EEOD码和STAR码每个数据位平均需要的小写操作为6-1/m次[7-8]，包括参与单次的校验列计算，每个块需要4次读写操作以及参与多次校验列计算的数据，则需要m+1次读写操作.

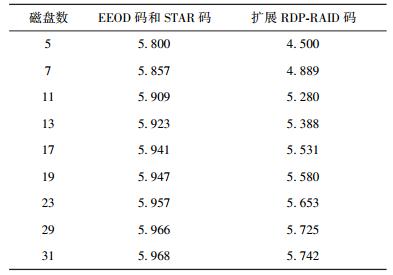
在扩展RDP-RAID码中，也分2种情况：① 参与多次校验列计算的数据位需要6次读写操作，共有(m-1)2-4(m-2) 个数据块；② 参与单列校验计算的数据位需要4次读写操作，共有4(m-2) 个数据块.因此，每个数据位平均需要小写操作6-8(m-2)/(m-1)2次. 表 2给出了3种纠删码更新复杂度比较.由表 2可看出，扩展RDP-RAID码的更新复杂度要低于另外2种纠删码，随着码的列数(磁盘数)增大，3种3容错编码的更新复杂度都接近6.但是，扩展RDP-RAID码一个数据块修改，只需要6次或者4次的读写操作，而另2种纠删码涉及多列需要m+1次读写操作，不涉及多列需要4次读写操作.由此可知, 扩展RDP-RAID码将更新负载操作均衡到每个数据位，有利于解决存储系统I/O问题，不易由于小写产生额外瓶颈.

表 2 3种纠删码每比特更新复杂度
3.4 平均数据丢失时间

在RAID系统中，平均数据丢失时间(MTTDL，mean time between data loss)是衡量存储系统可靠性最重要的一个参数[2-3].对于3容错的RAID系统，只有3个以上磁盘出现故障，数据才不可恢复.因此，MTTDL的计算式为

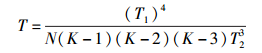
(14)

其中：T1为平均间隔故障时间，指2磁盘发生故障的平均间隔时间；T2为平均修复时间，指单个故障磁盘数据恢复时间；N为系统磁盘个数；K磁盘阵列分组.

编译码复杂度和更新复杂度越低，其平均间隔故障T1的值越小，而扩展RDP-RAID码的编译码复杂度和更新复杂度低于EEOD码和STAR码.若存储系统N和K相同，由式(14) 可知，其T1值越小，T值越小，可靠性越高，因此扩展RDP-RAID码为存储系统提供更高可靠性.

4 结束语

笔者提出了一类新扩展RDP-RAID码，不但可以允许任意3个设备失效，而且保留了RDP更新复杂度均衡特点，并且提出了基于二元比特矩阵编译码算法，实现简单直观.与EEOD码和STAR码性能进行比较，扩展RDP-RAID码的更新复杂度、编译码复杂度、存储效率综合性能更优，可靠性更高.

参考文献
[1] 罗象宏, 舒继武. 存储系统中的纠删码研究综述[J]. 计算机研究与发展, 2012, 49(1): 1–11.
Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J].Journal of Compute Research and Development, 2012, 49(1): 1–11.
[2] 宋杰, 李甜甜, 闫振兴, 等. 数据密集型计算中负载均衡的数据布局方法[J]. 北京邮电大学学报, 2013, 36(4): 76–80.
Song Jie, Li Tiantian, Yan Zhenxing, et al. Load balanced data layout approach in data intensive computing[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(4): 76–80.
[3] Blaum M, Brady J, Bruck J, et al. EVENODD: an efficient scheme for tolerating double disk failures in RAID architectures[J].IEEE Transaction on Computers, 1995, 44(2): 192–202. doi: 10.1109/12.364531
[4] Li Mingqiang, Shu Jiwu. C-codes: cyclic lowest density MDS array codes constructed using starters or RAID 6[EB/OL]. (2012-08-04)[2013-03-20]. http://arxiv.org/abs/1104.2547.
[5] Corbett P, English B, Goel A, et al. Row diagonal parity for double disk failure[C]//Proceedings of the Third USENIX Conference on File and Storage Technologies. San Francisco: the USENIX Association, 2004: 1-14.
[6] Wu Chentao, Wan Shenggang, He Xubin, et al. H-code: a hybrid MDS array code to optimize partial stripe writes in RAID-6[C]//Proceeding of the 25th IEEE Congress on International Parallel & Distributed Processing Symposium. USA: IEEE, 2011: 782-793.
[7] Huang Cheng, Xu Lihao. STAR: an efficient coding scheme for correcting triple storage node failures[J].IEEE Transaction on Computers, 2008, 57(7): 889–901. doi: 10.1109/TC.2007.70830
[8] 万武南, 吴震, 陈运, 等. RAID-EEOD:一种基于3容错阵列码RAID数据布局研究[J]. 计算机学报, 2007, 30(10): 1–10.
Wan Wunan, Wu Zhen, Chen Yun, et al. RAID-EEOD: the study of data placement based on toleration on triple failures array codes in RAID[J].Chinese Journal of Computers, 2007, 30(10): 1–10.
[9] Feng Guilian, Robert D, Feng Bao, et al. New efficient MDS array codes for RAID, part Ⅰ: reed-solomon-like codes for tolerating three disk filures[J].IEEE Transaction on Computers, 2005, 54(9): 1071–1080. doi: 10.1109/TC.2005.150