2. 华南理工大学 计算机科学与工程学院,广州 510006
针对因特网流量分类面临的流量类别标记瓶颈和类别样本数分布不平衡,提出基于Bootstrapping的流量分类方法,使用少量有标记样本训练初始分类器,迭代利用无标记样本扩展样本集并更新分类器.在构建扩展样本集过程中,将无标记样本在某后验概率分布下的正确分类行为视为一个概率事件,建立新的置信度计算方法,以减少扩展样本集中的噪声样本;基于概率近似正确学习理论建立启发式规则,注重选择小类样本加入扩展样本集,缓解类别样本数分布的不平衡.实验结果表明,与初始分类器相比,基于Bootstrapping的流量分类器总体分类准确率可提高9.46%;与现有半监督学习方法相比,小类分类准确率提高2.22%.
2. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510006, China
Aiming at the class labeling starvation and class imbalance problems in Internet traffic classification, a bootstrapping based traffic classification method was presented. An initial classifier was trained on a small number of labeled samples, and then it is updated iteratively by predicting the class labels of unlabeled samples and extending the training set. A new algorithm was devised to compute the confidence used for selecting new labeled samples into the extension set. It correctly adopts classifying unlabeled samples with a posterior probability distribution as probabilistic event and to decrease the noise in the extension set. Moreover, the heuristic rule was built with aid of probably approximately correct theory, its biases is toward selecting minority class samples into the extension set so as to reduce class imbalance degree. Experiments show that the bootstrapping based classifier gets improved of 9.46% on overall classification accuracy compared with initial classifier, and the recalls of minority classes get increased about 2.22% averagely compared with the existing method.
Internet流量分类成为网络协议研究和流量工程的重要基础.近年来,基于机器学习的流量分类成为流量分类领域的研究热点之一[1].此方法面临流量类别标记瓶颈和数据固有的类别分布不平衡两大挑战.
类别标记瓶颈表现为难以快速且准确地为大量网络流建立类别标签.基于载荷特征字段匹配的L7-filter方法无法实现加密流的类别标记,而人工标记方法又耗时耗力.针对此类问题,基于半监督学习的流量分类方法具有良好前景,因其能利用少量的有标记样本和大量无标记样本,训练有效的分类器. He等[2]在CoForest[3]基础上结合了集成学习方法,但是多个基分类器使用不同的属性子集,这些子集难以满足协同训练所要求的独立且充分冗余视图的性质.因特网流量分类面临的另一项挑战是类别分布不平衡,其表现为某些流量类别(大类, majority class)的样本数目显著高于其他类别(小类, minority class);分类器的分类性能往往偏向大类而忽略了小类.但是现有研究在无标记样本信息挖掘过程中,对数据不平衡关注不够,分类器对类别不平衡比较敏感[2,4].
笔者提出一种基于Bootstrapping的半监督流量分类方法(SITCMB, semi-supervised Internet traffic classification method based on Bootstrapping),利用Bootstrapping作为半监督学习算法,采用新的置信度计算方法和启发式规则,保证了扩展样本集的准确度和类别平衡度.
1 基础算法采用Bagging算法[5]作为集成分类算法,基于样本权重,有放回地自举抽样训练样例,以构建与原始训练集大小相同但样本各不相同的训练集,从而训练不同的基分类器,最终分类判决由基分类器投票执行.如算法1所示,Learn表示学习器,N表示输出的基分类器hi(i =1, 2,…, N)的个数,L表示训练集,L′表示从L中自举抽样的样本集,hf(x)表示最终输出的分类器.
算法1 Bagging算法

|
笔者选用Bootstrapping算法实现半监督学习,无须统计属性子集满足独立且充分冗余视图的性质.此算法利用少量有标记样本作为种子集训练初始分类器,并利用初始分类器分类无标记样本,建立新标记样本集;新标记样本集与种子样本集的并集训练新的分类器;迭代式循环,直到分类器的分类性能趋于稳定为止.如算法2所示,其中h(t)表示第t次输出的分类器,L表示种子样本集,U表示无标记样本集,UB表示新标记样本集.
算法2 Bootstrapping算法

|
给定有标记训练样本集L={(x1, y1), (x2, y2), …, (xL, y|L|)}和无标记训练样本集U={x′1, x′2, …, x′|U|}. xi由统计特征描述,y对应类别变量并具有q个离散值{c1, c2, …, cq}. SITCMB基于L和U建立样本到类别的映射函数f:X→Y.主要过程为:有标记样本集L训练初始集成分类器,分类器分类U的样本,迭代式建立扩展样本集并更新分类器.
新标记样本的类别标签由分类器预测得到,其中存在错误标记的样本.为保证扩展样本集中样本标记的正确性,通常为每个样本计算一个置信度(后验概率),并通过阈值选择置信度高的样本加入扩展样本集.集成分类器分类某个未知样本(如xj)的后验概率由投票方式计算,并将样本预测为后验概率最大的类别cm=argmax(p(ci|xj)).但是,由前期的实验结果观察得到,具有最大后验概率且后验概率大于置信度阈值的类别不一定是样本的真实类别.针对此问题,笔者提出新的置信度计算方法.
在某后验概率分布情况下,将样本分类正确视为一项概率事件.首先利用初始分类器分类某个测试样本集,记录每个测试样本的后验概率分布;当分类无标记样本时,计算在分类器输出的后验概率分布下,cm正确的概率.置信度的计算步骤如下.
1) 构建样本集Lc:有标记样本集L={x1, …, x|L|}用于训练集成分类器;对L的每个样本xj,采用集成分类器的投票结果计算将xj预测为每个类别的后验概率p(ci|xj) (i=1, …, q);对p(ci|xj)×10进行向下取整,并将结果作为属性值描述样本xjc,且xj的真实类别yj作为xjc的类别属性值.那么,xjc有q个属性,其属性集合表示为Ac={A1c, …, Aqc};所有新构建的样本xjc组成样本集合Lc(1≤j≤|L|).其中,对p(ci|xj)×10进行向下取整,旨在使得xjc的属性值为整数,并凸显概率分布的规律性,进而有利于提高第2) 步估算的p(x′kc|cm)的有效性.
2) 估算标记正确的概率:对于某个无标记样本x′k(k=1, …, |U|),根据集成分类器的投票结果计算将x′k预测为每个类别的后验概率p(ci|x′k) (i=1, …, q)和预测结果cm(用于标记x′k);与第1) 步类似,利用后验概率p(ci|x′k)建立样本x′kc.在x′k的后验概率分布下,将x′k标记正确的概率p(cm|x′kc)的估算如下.
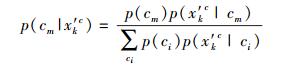
|
(1) |
其中,
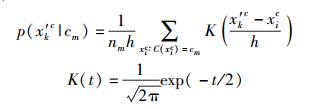
|
p(x′kc|cm)表示Lc集合中给定类别cm,x′kc的概率,这由高斯核函数估算得到;p(cm)表示Lc集合中cm的先验概率.
3) 计算置信度C:为提高置信度的可靠性,集成分类器输出的后验概率p(cm|x′k)也参与计算.将x′k预测为cm的置信度的计算如下.
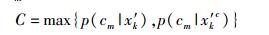
|
(2) |
尽管置信度计算方法能尽可能提高新标记样本的正确性,但是新标记样本中仍然存在错误标记的噪声样本.分类噪声比率可通过增加足够多的新样本得到补偿.基于可能近似正确(PAC, probably approximately correct)学习理论,Zhou等[6]推导出为使得第t次迭代的错误率上界小于第t-1次迭代的错误率上界,有标记样本集L,扩展样本集NL、有标记样本中的分类噪声率ηL和NL的分类噪声率(由集成分类器的错误率估算)之间的关系需满足不等式(3).假设0<et<et-1<0.5,为满足式(3),需满足|NLt-1|<|NLt|和et|NLt|<et-1|NLt-1|.当et<et-1且|NLt-1|<|NLt|,et|NLt|<et-1|NLt-1|不一定满足,其原因是|NLt|可能远远大于|NLt-1|,此时需从NLt中采样et-1|NLt-1|/et个样本.其中et的估算方式是将未选入训练样本集的有标记样本作为测试样本集,检验分类器的错误率.
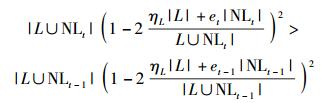
|
(3) |
另外,由于流量数据中大类总是拥有绝大部分的样本,然而小类的样本数极少.分类器总是偏向正确分类大类样本,而忽略了小类的分类性能.在建立NL中,选择大类样本的概率大于小类的概率,导致NL中样本存在类不平衡.针对此问题,为构建NL建立以下启发式规则.规则1:将置信度大于阈值δ的所有样本选入第t次迭代的临时样本集Ltmpt.规则2:利用不等式(3)计算第t次迭代的扩展样本集的下限(nmint),统计Ltmpt中小类样本数nst,若nst>nmint,则从小类样本中随机选取nmint样本加入NLt,若nst<nmint,则将所有小类样本选入NLt,并另外随机选取(nmint-nst)的大类样本加入NLt.规则1保证扩展样本集中的样本标记尽可能正确;规则2加强扩展样本集中的小类样本,进而缓解类不平衡.
分别从分类器训练和分类器分类2个部分对SITCMB进行描述. 1)~6) 为分类器训练部分,最后对分类器分类进行简要叙述.
1) 训练初始分类器:迭代次数变量t=1,将L输入Bagging学习器得到集成分类器h1.
2) 记录最佳分类器:第t次迭代的分类器ht分类评测样本集(由未选入训练样本集的有标记样本组成),统计分类错误率et,判断et<emin(emin的初始化值为e0)是否满足,若满足则hbest=ht且emin=et;否则不作任何操作.
3) 终止条件判断:判断|et-et-1|<0.001和t是否达到迭代次数阈值θ,若满足其中之一则进入第6) 步;否则进入第4) 步.
4) 构建扩展样本集NLt:使用ht分类U中的样本,得到无标记样本的类别,可得新标记样本集为Lu={(x1, y1), …, (x|U|, y|U|)},计算新标记样本的置信度,并根据2个启发式规则建立NLt.
5) 更新分类器:将L∪NLt用于重新训练集成分类器,获得第t+1次的分类器ht+1,t=t+1然后进入第2) 步.
6) 循环终止,输出最终分类器hbest.
当最终分类器分类某个未知样本时,根据集成分类器中基分类器的投票结果进行分类.
3 实验验证3.1 实验设计实验数据为剑桥大学共享的因特网流量数据,包括3个独立的数据集:Day1、Day2和Day3[7].该数据来自某研究中心,该中心拥有上千名员工,包括研究员、管理员和技术员,通过千兆全双工以太网链路连接因特网.从该中心采集了3天的流量记录,分别来自于2003、2004和2006年度的某个周末.每个流样本由12个流统计属性描述,数据集的描述详见文献[7].
实验验证包括基本流量分类性能、流量分类鲁棒性和小类分类性能的比较.为了与CoForest[2]方法比较,构建训练集的方法与其一致.训练样本集中有标记样本的比例(LR, labeled rate)包括4种情况:LR为20%、LR为40%、LR为60%和LR为80%.基础分类算法选用随机树.在每种情况下,执行20次完整的SITCMB和CoForest,最后输出平均结果.分类性能指标包括:单类分类准确率和总体分类准确率,它们都以流为单位统计,以百分数给出. SITCMB算法的参数:初始错误率e0=0.5;置信度阈值δ=0.8;Bagging算法中的参数N=6.
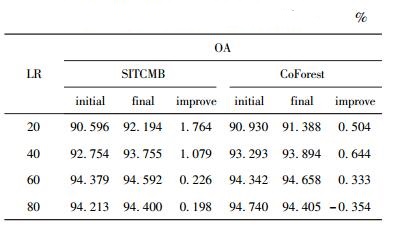
3.2 流量分类性能比较实验分别在Day1、Day2和Day3上进行. 3个数据集的实验结果类似,下面仅给出Day1上的实验结果,如表 3所示. initial表示初始分类器的分类结果,final表示最终分类器的分类结果,improve表示总体分类准确率(OA,overall accuracy)的提高率.表 1表明,SITCMB的最终分类器与初始分类器相比,OA都有提高.与CoForest相比,SITCMB在大部分情况下对OA的提高率更高,这是因为SITCMB的置信度计算方法结合了流量分类的先验信息,有利于保障扩展样本集中的样本质量,提高无标记样本信息的利用率.
|
|
表 1 Day1 上的总体分类准确率比较 |
流量分类鲁棒性关注的是,随着时间的推移,分类器的分类稳定性情况.实验要求训练集和测试集相隔数月,即Day1作为训练样本集,Day2和Day3作为测试集.
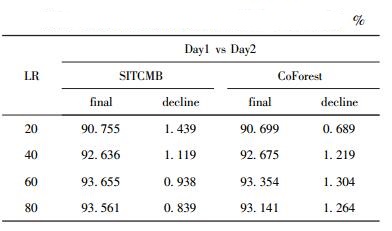
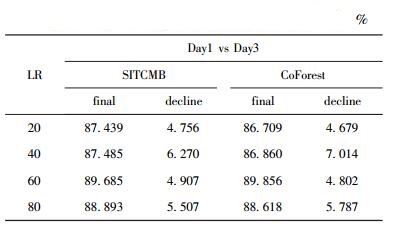
表 2和表 3分别是最终分类器在Day2和Day3测试集上的总体分类性能,decline表示最终分类器的OA相比表 1的最终分类器的降低度.与CoForest相比,SITCMB的OA在大部分情况下降低更小.因为SITCMB的“启发式规则1”使得扩展样本集的质量有所保障.某些情况下SITCMB的OA降低程度较大,是因为“启发式规则2”趋向于选择小类样本,但是小类分类准确率对OA的贡献度低.
|
|
表 2 Day1 vs Day2 上的总体分类准确率比较 |
|
|
表 3 Day1 vs Day3 上的总体分类准确率比较 |
以Day1 vs Day2为例,验证2种方法在处理类别不平衡上的性能.表 4和表 5分别是SITCMB和CoForest在4种LR下的平均分类结果. SITCMB对大部分小类样本取得了较高的分类准确率. CoForest对某些类别的小类样本也有较高的分类准确率,这是因为种子样本集是由每类300个样本组成,即训练样本集相对平衡,不会造成分类器的分类性能有很大的偏斜. SITCMB对某些小类样本的分类准确率显著高于CoForest,例如DATABASE达到了40.67%(CoForest仅有20.54%).
|
|
表 4 SITCMB 的单类分类准确率 |
|
|
表 5 CoForest 的单类分类准确率 |
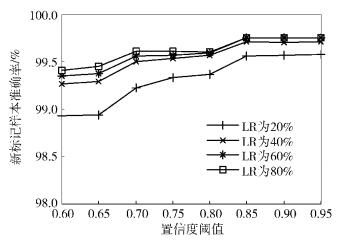
1) 置信度阈值:在SITCMB训练分类器的迭代过程中,分类器分类无标记样本,并选取置信度大于某个阈值的新标记样本加入扩展样本集.置信度表示将无标记样本标记正确的概率.为保障新标记样本有较高的置信度,此参数的最小值为0.6,其取值范围为0.6~0.95,实验结果如图 1所示. x轴表示置信度阈值,y轴表示新标记样本的总体准确率.
|
图 1 置信度阈值参数讨论 |
在4种LR情况下,新标记样本的准确率都随着阈值的增加而提高.这有利于减少扩展样本集的噪声样本,进而提高分类器的分类性能.当参数值大于0.8,流标记准确率能达到99.3%;进一步增加阈值,流标记准确率能达到99.5%.置信度阈值过高可能导致仅有少量新标记样本符合此条件,难以有效更新分类器.因此笔者选取0.8为适当的中间值.
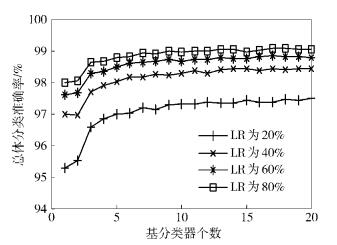
2) 分类器个数:基分类器个数是SITCMB的集成分类器中的单个分类器数目.此参数的取值范围为1~20,实验结果如图 2所示,x轴表示分类器个数,y轴表示总体分类准确率.与理论一致,在4种LR情况下,分类准确率都随着分类器个数的增加而提高,当分类器个数达到某个取值之后,分类性能趋于稳定.当分类器个数为6时,分类性能基本稳定.
|
图 2 基分类器个数讨论 |
基于Bootstrapping算法,提出一种半监督流量分类方法SITCMB.该方法将新的置信度计算方法与PAC学习理论相结合构建启发式规则,以挖掘无标记样本信息和缓解类不平衡.与CoForest[2]和半监督SVM[4]相比,SITCMB的优势表现为:将样本在某个后验概率分布下预测正确视为一项概率事件,并基于此提出置信度计算方法,提高扩展样本集中正确标记样本的比率;在建立扩展样本集中注重选取小类样本,进一步缓解类不平衡问题.在真实流量数据集上的多项实验结果表明,SITCMB可有利改善分类器的分类能力和泛化能力,并且在分类小类样本方面更优.今后还将在多方面继续深入研究,例如将SITCMB用于在线分类、半监督流量分类下的特征选择算法、半监督流量分类算法的比较.
| [1] |
林平, 余循宜, 刘芳, 等. 基于流统计特性的网络流量分类算法[J]. 北京邮电大学学报, 2008, 31(2): 15–19.
Lin Ping, Yu Xunyi, Liu Fang, et al. A network traffic classification algorithm based on flow statistical characteristics[J].Journal of Beijing University of Posts and Telecommunications, 2008, 31(2): 15–19. |
| [2] | He Haitao, Luo Xiaonan, Ma Feiteng, et al. Network traffic classification based on ensemble learning and co-training[J].Science in China Series F:Information Sciences, 2009, 52(2): 340–341. |
| [3] | Li Ming, Zhou Zhihua. Improve computer-aided diagnosis with machine learning techniques using undiagnosed samples[J].IEEE Transactions on System, 2007, 19(11): 1479–1493. |
| [4] | Li Xiang, Qi Feng, Xu Dan, et al. An Internet traffic classification method based on semi-supervised support vector machine[C]//Proceedings of IEEE International Conference on Communications, Cape Town. South Africa:IEEE Press, 2011:1-5. |
| [5] | Breiman L. Bagging predictors[J].Machine Learning, 1996, 24(2): 123–140. |
| [6] | Zhou Zhihua, Li Ming. Tri-training:exploiting unlabeled data using three classifiers[J].IEEE Transactions on Knowledge and Data Engineering, 2005, 17(11): 1530–1531. |
| [7] | Li Wei, Cannini M, Moore A W, et al. Efficient application identification and the temporal and spatial stability of classification schema[J].Computer Networks, 2009, 53(6): 790–809. doi: 10.1016/j.comnet.2008.11.016 |