2. 济宁学院 计算机科学系, 山东 曲阜 273155;
3. 北京京开投资开发股份有限公司 低碳研究中心, 北京 100176
防冲突技术是无线射频识别(RFID)系统中的关键技术.针对二进制搜索防冲突算法读取海量数据标签效率低的问题,通过分析标签数量为海量数据的特征以及标签编码的规律性,基于管理系统中海量数据标签的编码规律和现有二进制搜索算法思想,提出了适合于读取海量数据RFID标签的扁平N叉树搜索防冲突算法.测试结果表明,该算法在标签总数大于一定数值时,其读取标签效率优于二进制搜索算法.
2. Department of Computer Science, Jining University, Shandong Qufu 273155, China;
3. Low-carbon Research Center, Beijing Development Area Co, Beijing 100176, China
The anti-collision technology is a key technology in the radio frequency identification (RFID) system. In order to avoid the low efficiency problem of reading massive data labels via the binary-tree search algorithm, by analyzing the character of mass data and the regularity of tags encoding, a flat-N-tree search anti-collision algorithm is proposed according to the regularity of massive data tags encoding and the principle of binary-tree search algorithm in the management systems, which is suitable for reading massive data RFID labels. The result shows that the reading efficiency of the multi-tree search algorithm is better than that of the binary-tree search algorithm when the total quantity of tags is greater than a certain value.
RFID技术是一种非接触的自动识别技术,其基本原理是利用射频信号的空间耦合传输特性,实现对目标物体的自动识别[1].通常,工作在同一RFID系统中所有的电子标签具有相同的工作频段.当读写器作用范围内存在多个电子标签,且在同一时刻有多个电子标签发送信息到达读写器时,就会出现信息的互相干扰,使得读写器不能正确识别电子标签的信息,于是就产生RFID电子标签冲突.防冲突算法所研究的关键问题是解决如何快速、准确地从多个电子标签中识别出一个标签并与读写器进行数据信息交互,而此次未被选中的电子标签在后续防冲突算法的循环过程中陆续被识别选出并与读写器进行信息交互[2-3].
目前,RFID系统防冲突算法主要有ALOHA算法[4]和二进制搜索算法[5-7].基于二进制搜索防冲突算法是通过曼彻斯特编码来识别发生冲突的具体位置,从而将读写器作用范围内的标签划分为更小的集合来解决防冲突问题.该类算法因其识别效率较高、吞吐量大,而被广泛应用于RFID系统中[5-7].针对二进制搜索算法对于海量数据的读取存在着读写器请求次数过多及标签回传数据量过大等问题,笔者在二进制搜索算法的基础上,提出了适合于海量数据的RFID扁平N叉树防冲突算法,该算法对于标签海量数据的读取具有请求次数少、识别标签速度快等优点.
1 二进制搜索算法二进制搜索算法的主要思想是通过读写器发送命令给所有标签,符合要求的标签都返回给读写器一定的信息,读写器根据所获得的信息判断标签是否有冲突,如果有冲突就继续发送识别命令,如果没有冲突就识别出某个确定的标签,直至将所有标签都识别出来.其具体步骤:对每次识别的冲突位进行分类,分成0、1两部分,形成一棵二叉树,其正确识别出来的标签均位于二叉树的叶子结点.如果标签的总数目为M,则根据二叉树性质可知二叉树的非叶子结点数为M-1,而这些非叶子结点正是二进制搜索算法识别标签时发出的无效指令,因而M-1即为二进制搜索算法中读写器识别标签所发出的无效指令次数.
RFID系统防冲突算法是通过读写器与电子标签之间的通信来实现的.衡量一个RFID系统防冲突算法的优劣往往就是从通信过程中的识别效率入手来考虑的.其中,标签的识别效率最重要的是读写器发送多少次指令才能正确识别出标签,也就是读写器识别所有电子标签所需要传输指令的次数.减少读写器的识别次数就能减少读写器和标签的功耗,从而增加其使用寿命,同时也减少了识别时间.所以通过减少读写器识别标签所发送指令的次数可以有效减少识别时间,提高识别效率.但是,面对海量数据读取时,二进制搜索算法的读写器传输次数过多会导致读写器读写效率降低.
2 扁平N叉树防冲突算法2.1 算法思想扁平N叉树防冲突算法的基本思想如下.
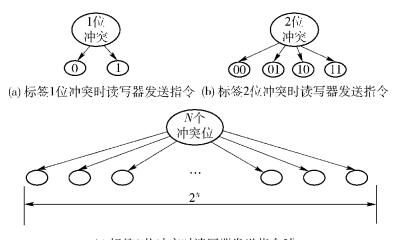
1) 读写器向所有标签发送指令,当标签有1位发生冲突时,读写器将21个指令1和0发出识别标签,如图 1(a)所示.
|
图 1 标签位冲突示意图 |
2) 当标签有2位发生冲突时,读写器将4(22)个指令00、01、10、11发出识别标签,如图 1(b)所示.
……
当标签中有N位发生冲突时,读写器将标签发生冲突位的全部2N个情况以指令的形式发出,依次来识别标签,如图 1(c)所示.
2.2 算法指令扁平N叉树防冲突算法的指令集如下.
1) REQUEST(缩写为Q):请求命令.其命令形式为Q(ID),其参数为与标签ID长度相同的二进制数.读写器通过该命令将ID号作为参数发送给标签,标签收到该命令后,如果标签不是处于静默状态,那么标签返回自身的ID号.
2) SELECT(缩写为SEL):选择命令.其命令形式为SEL(ID),其参数为电子标签的ID号. SELECT命令是使与ID参数值相同的标签做出响应而被选中,以此作为执行读取或写入的命令开关.其他标签对此不做响应.
3) READ:读取命令.其命令形式为READ(ID),其参数为电子标签的ID号.读写器需要读取数据的电子标签首先通过SELECT命令加以选择,当收到读写器发送的READ命令时,该标签将自身存储的数据等信息发送给读写器.
4) UNSELECT(或缩写为UN):去选择命令.其命令形式为UNSELECT(ID),其参数为电子标签的ID号.该命令的发送是在READ命令读取数据之后,当电子标签收到读写器发送的该命令后,即进入“休眠”状态.
2.3 算法流程算法流程图如图 2所示.

|
图 2 扁平N叉树防冲突算法流程 |
下面通过一个具体的实例来说明扁平N叉树算法操作的具体流程.设定实例标签的ID位数为4位,共10个标签,分别是1001、0110、0101、1101、0011、0100、0001、0010、1000、1010.其识别过程如图 3所示.

|
图 3 扁平N叉树搜索算法识别过程 |
1) 首先读写器发送命令Q(1),ID小于1111的电子标签返回其ID号,读写器接收到的结果是XXXX.
2) 判断读写器接收到标签响应,并且标签有冲突位,冲突的位数为4,读写器继续发送16(24)个指令0000、0001、0010、0011、0100、0101、0110、0111、1000、1001、1010、1011、1100、1101、1110、1111.
3) 10个标签1001、0110、0101、1101、0011、0100、0001、0010、1000、1010分别响应参数相同的读写器指令SEL(ID),即读写器选中与其参数一致的标签.
4) 读写器读写已选中的标签READ(ID).
5) 读写器将已读写的标签依次置为静默状态UN(ID).
6) 算法结束.
3 算法分析3.1 读写器发送指令数比较分析当有M个标签且有N个冲突位时,在二进制搜索算法中,读写器发送M-1个无效指令;在扁平N叉树防冲突算法中,读写器发送的无效指令数为2N+1-M.
当M-1=2N+1-M,M=(1/2)×2N+1时,即当二进制搜索算法读写器发送的无效指令数等于扁平N叉树算法读写器发送的无效指令数时,也即当标签的数目等于标签冲突数的一半加1时,扁平N叉树算法与二进制搜索算法识别标签的效率持平.
当M-1>2N+1-M,M>(1/2)×2N+1时,可知,当二进制搜索算法读写器发送的无效指令数大于扁平N叉树算法读写器发送的无效指令数时,即当标签的数目大于标签冲突数的一半加1时,扁平N叉树算法识别标签的效率优于二叉树算法的效率.
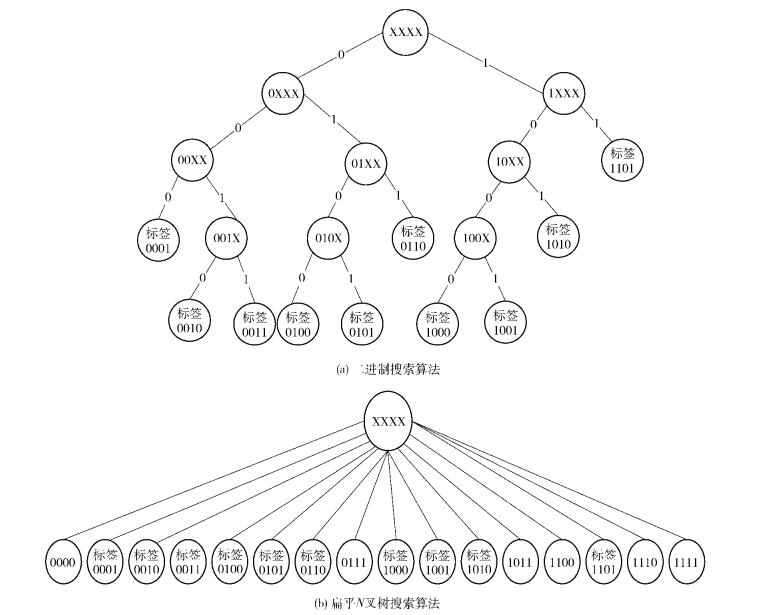
以标签1001、0110、0101、1101、0011、0100、0001、0010、1000、1010为例,其冲突位有4位为XXXX,二进制搜索算法的查询过程如图 4(a)所示.
|
图 4 二进制和扁平N叉树搜索算法查询图 |
由图 4(a)可以看出,二进制搜索算法识别所有标签的无效指令为9(10-1) 个. 10个标签用扁平N叉树搜索算法的搜索过程如图 4(b)所示.由图 4(b)可以看出,扁平N叉树搜索算法识别所有标签的无效指令为7(24+1-10) 个.
对比2种算法,当冲突位数为4,标签数为10>9 ((1/2)×24+1) 时,扁平N叉树搜索算法识别所有标签的无效指令数7小于二叉树搜索算法识别所有标签的无效指令数9,故扁平N叉树搜索算法识别效率较高.
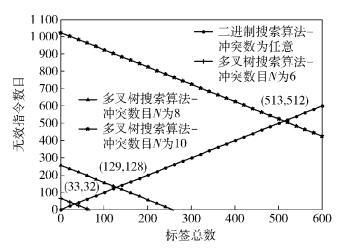
按照二进制搜索算法识别标签的无效指令数目Y=M-1,扁平N叉树搜索算法识别标签的无效指令数目Y=2N+1-M,画出2种算法的关系图,如图 5所示.
|
图 5 二进制和扁平N叉树搜索算法识别标签的无效指令函数图 |
由图 5可以看出,二进制搜索算法中随着标签数的增长,读写器识别标签所发送的无效指令数在不断增大;而扁平N叉树搜索算法正相反,随着标签数的增长,读写器识别标签所发送的无效指令数不断减小.而且,二进制搜索算法只与标签个数M有关,扁平N叉树搜索算法与标签个数M和冲突位数N均有关,以图 5的冲突数N为8来说明,当冲突数为8位,识别标签总数达到129个时,2种算法的无效识别数相同都为128,此时2种算法的识别效率一致;当冲突位N为8位,识别标签数大于129时,从图 4(b)可以看出,扁平N叉树搜索算法的无效指令数少于二进制搜索算法的无效指令数.
3.2 识别标签时间分析当标签数目为M,冲突数为N时,二进制搜索算法识别标签的总时间为T1=2M-1,扁平N叉树搜索算法识别标签的总时间为T2=2N+1.
当T1=T2即M=(1/2)×2N+1时,2种算法识别M个标签所用的时间相同.
那么,当T1>T2即M>(1/2)×2N+1时,二进制搜索算法识别标签的时间大于扁平N叉树搜索算法的识别时间,此时扁平N叉树的识别速度快.同时,这一规律与3.1节中所述当M>(1/2)×2N+1时,二进制搜索算法读写器发送无效指令数大于扁平N叉树搜索算法读写器发送无效指令数的规律一致,即当M>(1/2)×2N+1时,扁平N叉树搜索算法无论是在发送无效指令数上还是在识别速度上都优于二进制搜索算法.
由此可见,在标签数达到一定数量(M>(1/2)×2N+1) 时,扁平N叉树搜索算法的识别效率高于二进制搜索算法的识别效率.
4 扁平N叉树搜索防冲突算法在仓储系统中的应用分析4.1 电子产品码EPC(electronic product code)标签特点在仓储系统中,(EPC)标签是一种应用特殊产品编码形式来编码的标签,每个EPC标签唯一标识一个产品. EPC标签代码由“头字段”、“EPC管理者”、“对象分类”和“序列号”4个域构成.其中“头字段”、“EPC管理者”和“对象分类”字段信息在仓储系统基本不变,从而这些字段冲突的可能性小,而主要的冲突发生在产品的“序列号”字段上.
4.2 算法在仓储系统中的应用分析通常在仓储系统中,海量的标签数目意味着M的值会很大,这样将二进制搜索算法应用在仓储系统中读写器识别标签所发送无效指令数目M-1也将会很大.所以,二进制搜索算法不适合应用于仓储系统中海量数据的读取.而扁平N叉树搜索算法比较适合仓储系统的海量标签情况.下面将扁平N叉树搜索防冲突算法应用在仓储系统中进行分析,读写器发送指令的情况如图 6所示.

|
图 6 仓储系统中扁平N叉树搜索算法识别标签过程 |
由图 6可知,当仓储系统中有M个标签且有a1、a2、a3、…、an段冲突位发生时,利用扁平N叉树防冲突算法,读写器发送指令数为2a1+a2+a3+…+an,其中无效指令数为2a1+a2+a3+…+an+1-M,比较二进制搜索算法读写器发送的无效指令数M-1,当M-1>2a1+a2+a3+…+an+1-M,即M>(1/2)×2a1+a2+a3+…+an +1时,也即当标签的数目M大于标签冲突数2a1+a2+a3+…+an的一半加1时,扁平N叉树算法读写器发送有效指令次数大于二进制搜索算法中读写器发送的有效指令数,此时扁平N叉树算法识别标签的效率较高.在仓储系统中由于标签具有海量的特点,即标签数目M的值较大,比较适合应用扁平N叉树搜索防冲突算法.
5 结束语提出了一种适合于海量数据标签的扁平N叉树搜索防冲突算法,通过数学推理和仓储系统中的应用对该算法和二进制搜索算法进行比较,得出了扁平N叉树搜索算法在面对海量数据的情况下,读写器所需发送的总请求次数T(N)以及读写速度等性能方面都要优于目前的二进制搜索算法,在很大程度上减少了读写器发送的总请求次数,有效地提高了标签的识别速度,降低了功耗,对于解决现有仓储RFID系统中的防冲突问题有着重要的意义.
| [1] | |
| [2] | Eom J B, Lee T J. An efficient framed-slotted ALOHA algorithm with pilot frame and binary selection for anti-collision of RFID tags[J].IEEE Communications Letters, 2008, 12(11): 861–863. doi: 10.1109/LCOMM.2008.081157 |
| [3] |
胡桂兵, 邱雪松, 孟洛明. 基于信号稳定度提高RFID识别率的方法[J]. 北京邮电大学学报, 2012, 35(1): 55–58.
Hu Guibing, Qiu Xuesong, Meng Luoming. An efficient method for RFID's discrimination stability[J].Beijing University of Posts and Telecommunications, 2012, 35(1): 55–58. |
| [4] |
袁开国, 郝昱文, 李争平, 等. RFID网络中基于Aloha防碰撞的标签数目的联合估计算法[J]. 北京邮电大学学报, 2014, 37(Sup): 72–76.
Yuan Kaiguo, Hao Yuwen, Li Zhengping, et al. A hybrid tag number estimation scheme for Aloha based anti-collision algorithm in RFID networks[J].Journal of Beijing University of Posts and Telecommunications, 2014, 37(Sup): 72–76. |
| [5] |
谢磊, 殷亚凤, 陈曦, 等. RFID数据管理:算法、协议与性能评测[J]. 计算机学报, 2013, 36(3): 457–470.
Xie Lei, Yin Yafeng, Chen Xi, et al. RFID data management: algorithms, protocols and performance evaluation[J].Chinese Journal of Computers, 2013, 36(3): 457–470. |
| [6] |
杜海涛, 徐昆良, 王威廉. 基于返回式二进制树形搜索的反碰撞算法[J]. 云南大学学报:自然科学版, 2006, 28(S1): 133–136.
Du Haitao, Xu Kunliang, Wang Weilian. An anti-collision algorithm based on binary-tree searching of backtracking[J].Journal of Yunnan University: Natural Sciences Edition), 2006, 28(S1): 133–136. |
| [7] | Djeddou M, Khelladi R, Benssalah M. Improved RFID anti-collision algorithm[J].Aeu-international Journal of Electronics and Communications, 2013, 67(3): 256–262. doi: 10.1016/j.aeue.2012.08.009 |


