针对欠定情况下的快速跳频信号的参数估计问题,在基于自回归滑动平均(ARMA)模型的跳变点检测方法的基础上,提出了一种改进的快速跳频信号参数盲估计算法.通过跳周期修正ARMA模型预测点和傅里叶变换分别得到准确的跳变时刻和载频估计,从而实现快速跳频信号的参数估计.实验结果表明,该算法在欠定条件下,当信噪比大于10 dB时,相对现有算法跳变点检测准确率增加了5倍左右,检测准确的概率可以达到90%以上.
Aiming at the parameter estimation of the fast frequency hopping signals for underdetermined situation, an improved blind parameter estimation algorithm was proposed, considering the hopping instants detection method based on autoregressive moving average (ARMA) model. The parameter estimation of the fast frequency hopping signals was realized by modifying the time-hopping sequence according to the hop duration and Fourier transform. Experiments show the estimation accuracy of the algorithm can reach more than 90%, about five times increasing compared with the existing algorithm for underdetermined situation when the signal to noise ratio is greater than 10 dB.
不同于一般的通信信号,跳频信号的载频是不断发生变化的,是一种非平稳信号,对干扰方来说,要实施干扰就必须估计出跳频信号的参数.对于一般的跳频信号,可以通过时频分析[1]和跳频信号时频域稀疏性的特点估计出跳频信号的参数,如平滑伪Wigner-Ville分布(SPWVD,smoothed pseudo Wigner-Ville distribution)[2]、短时傅里叶变换(STFT,short time Fourier transform, )[3]、小波变换、Gabor变换等.但是这些基于时频分析的方法往往存在时间分辨率和频率分辨率不可兼得的问题,而且大多数文献给出的算法只适用于慢速跳频信号的参数估计[4]. Liu等[5]提出了一种基于ARMA模型的跳变时刻和载频估计算法,该算法解决了时间分辨率和频率分辨率不可兼得的问题,但对信噪比和观测信号个数有一定要求,并要求已知源信号个数,然而在实际中,源信号数目一般是未知的,对于观测信号数目小于源信号数目的欠定条件,该算法失效.
本研究基于文献[5],针对上述不足,提出一种由跳周期来修正跳变时刻的方法,减少了虚检和漏检,在欠定混合情况下,算法性能得到显著提高.此外,在估计频率时,采用傅里叶变换,不管是抗噪声性能还是估计准确度都得到一定提高.
1 基于ARMA模型的跳频参数估计同步正交跳频信号接收场景如图 1所示,通过天线阵列,得到由未知数目的跳频信号混合而成的观测信号,观测信号数目与接收天线数目相同.

|
图 1 同步正交跳频信号接收场景 |
根据跳频信号的产生原理,在采样时刻t,观测信号模型可表示如下[5]
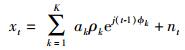
|
(1) |
其中:K为跳频信号数目;nt为t时刻噪声;ρk由t时刻第k个跳频信号的振幅和初相组成;ak=[1, ejφk, …, ej(M+1)φk]T,ϕk=2πfkDcosθk/C,θk表示第k个跳频信号的方向角,fk为t时刻第k个信号的载频,D为接收天线之间的距离,C=3×108 m/s为光速;φk=2πfkTs,Ts为采样时间间隔.
根据ARMA模型,th时刻的信号可由前K个时刻的信号来预测
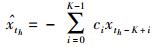
|
(2) |
K为ARMA模型阶数,文献[5]中取值为源信号数目.当频率发生跳变时,由于信号不再平稳,预测误差就会变大,所以可以通过检测预测误差来估计跳变时刻,即当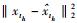
门限γ按如下公式选取
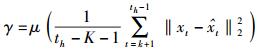
|
(3) |
其中μ一般取3~5[6].
因此要按照上述理论来估计跳变时刻,首先得建立一个ARMA模型,所以必须先确定ARMA模型的系数c.具体估计方法参考文献[5].
在已知c的情况下,令α=ejφk,它与ARMA模型的系数c满足如下方程
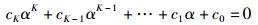
|
(4) |
其中cK=1.解上述方程求得α,从而得到φk,根据φk=2πfkTs,可以得出载频的估计值.
文献[5]中,上述结果是在假设ρk不变的条件下得到的,即在进行处理的时间段内码元保持不变,所以该算法适用于快速跳频信号.
2 基于跳周期的跳频时刻修正与频率估计方法在实际中,上述条件往往不能满足,再加上信噪比和观测信号数目等因素的影响,在跳变点检测时,经常会出现虚检和漏检.基于上述原理,笔者提出一种修正方法:在用ARMA模型得到跳时估计以后,考虑到对于快速跳频信号进行处理时,可以一次处理较多跳的数据.假设得到的跳变时刻序列为[t1, t2, t3, …, ti],首先对检测出的跳变时刻序列中的相邻两个时刻前后作差得到[t2-t1, t3-t2, …, ti-ti-1],然后按照相互之间的距离大小对这些差值聚类,将距离比较近的差值聚为一类,如果大部分的差值都聚为一类,那么取这一类中所有差值的均值作为跳周期估计值T.若t2-t1的值接近于T,那么取t1和t2作为新的跳变时刻,依次选出所有新的跳变时刻.假设得到的新的跳变时刻序列为[t1, t2, t4, …, ti],如果在两个跳变点之间的间隔大于一个跳周期,如(t4-t2)>T,那么在t2和t4之间加上漏掉的点t2+T,如果t1-T>0或者ti+T<t(t为观测信号的数据长度),那么加上漏掉的跳变点t1-T或者ti+T,从而减少虚检和漏检的存在.
此外,在文献[5]中,选取ARMA模型的阶数要与源信号数目相同,但是在实际中ARMA模型的阶数如果增大,预测反而会更加准确,所以完全不用将模型阶数固定为源信号数目,这样免去计算源信号数目,在一定程度上简化了算法.但是这样会导致文献[5]中频率估计方法错误,所以在估计频率时,本研究采用如下方法:分别对每一跳信号作傅里叶变换,找出傅里叶变换中最大的值Amax,然后取一合适系数λ(λ<1),找出傅里叶变换中大于λAmax的值,将这些值按照距离远近聚类,如果在某些类中包含的点数够多,那么对这些类中的所有点分别取平均值作为频率的估计,按照上述方法,即可得出所有跳的频率估计.
3 算法仿真与分析在进行参数估计时,取跳频信号数目为4,到达角分别为20°、60°、40°、80°,接收天线为均匀线阵,天线间距取半波长,码元速率分别为20 kHz,50 kHz、20 kHz、40 kHz,跳速为10万跳/s,采样频率fs=20 MHz,每个跳周期内采样点数为200,一共处理10跳的数据.
频率估计相对误差按照式(5) 计算:
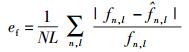
|
(5) |
其中:fn, l表示第n个源信号第l跳的频率真实值,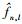
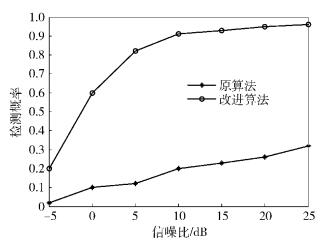
为了对比在欠定情形下,改进算法与文献[5]中算法(以下简称原算法)的性能,图 2给出了观测信号数目为2,源信号个数为4,模型阶数为4时,改进算法与原算法在不同信噪比下的跳变时刻检测概率性能对比.可以看出,原算法在观测信号数目小于源信号数目,即观测信号数目小于4的欠定情况下,算法检测概率性能恶化严重.而经过本研究改进以后,在欠定条件下,算法性能得到较大提高.在信噪比为0 dB左右时,改进算法准确度与原算法相比提高了5倍左右.
|
图 2 信噪比对检测概率的影响 |
图 3给出了信噪比为20 dB,观测信号数目为4,源信号数目为4,两种算法跳变时刻检测概率随模型阶数变化的曲线.从图中可以看出,模型阶数对原算法的性能有一定的影响,但是对于改进算法影响并不大,所以在进行改进算法仿真实现时,并不需要事先确定源信号数目.

|
图 3 模型阶数对检测概率的影响 |
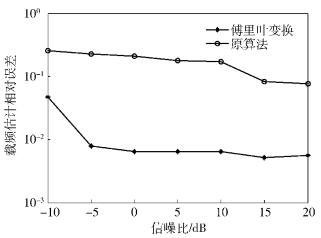
为了保证原算法估计准确,图 4给出了在观测信号数目为12,源信号数目和模型阶数取4的情况下,傅里叶变换估计的频率与原算法的性能对比.可以看出,原算法对噪声环境比较敏感,随着信噪比的降低,估计误差变化明显.在信噪比为-5 dB时,改进算法载频估计相对误差减小2个数量级.
|
图 4 信噪比对频率估计的影响 |
设ARMA模型阶数取K,观测信号数目为m,ARMA模型进行预测的过程进行了P次循环,总共处理A跳信号,求载频时傅里叶变化长度取B,那么原算法的复杂度为P(2K3+2mK2+K2+2Km+4m),在原算法的基础上,改进算法所增加的复杂度包含利用跳周期修正跳变时刻和快速傅里叶变换求载频两部分.前者是一个关于跳数n的线性阶O(n), 基本可以忽略,后者的复杂度为ABlb(B).在实际仿真中,K、m、P、A、B的取值分别为4、12、1 970、10、1 024,改进算法的复杂度与原算法相比大约增加了7.7%,在相同条件下,原算法和改进算法仿真花费时间分别为0.283 0 s和0.308 0 s,复杂度增加了8%左右.可以看出,改进算法在增加少量复杂度的基础上,带来了性能上大约5倍的提升.
5 结束语在文献[5]中提出的基于ARMA模型的跳变时刻检测算法的基础上,提出了一种新的快速跳频信号参数估计算法,该算法利用跳周期T来进行跳变点的修正,并通过增加ARMA模型阶数的方式使算法性能得到了改善.在欠定条件下,算法跳变时刻检测准确度增加了5倍以上.而关于频率估计方面,傅里叶变化比原算法估计更准确,结果表明, 本研究给出的频率估计方法的误差大大减少,在信噪比为-5 dB时,载频估计误差减少2个数量级.
| [1] | Yang Wenge, Li Meng, Wang Libin, et al. Parameter estimation of frequency hopping signals based on time frequency analysis[C]//Proceedings of the 26th Conference of Spacecraft TT & C Technology in China. Beijing: Tsinghua University Press, 2013: 131-140. |
| [2] | Chen T C. Joint signal parameter estimation of frequency-hopping communications[J].IET communications, 2012, 6(4): 381–389. doi: 10.1049/iet-com.2010.0318 |
| [3] | Li Tong, Tang Yinhui, Lv Jun, et al. Parameter estimation of FH signals based on STFT and music algorithm[J].2010 International Conference on Computer Application and System Modeling, 2010(5): 232–236. |
| [4] |
狄慧, 刘渝. Costas跳频信号参数盲估计算法研究[J]. 系统工程与电子技术, 2012, 34(3): 444–450.
Di Hui, Liu Yu. Research on parameter blind estimation algorithm of costas frequency hopping signals[J].Systems Engineering and Electronics, 2012, 34(3): 444–450. |
| [5] | Liu Z M, Huang Z T, Zhou Y Y. Hopping instants detection and frequency tracking of frequency hopping signals with single or multiple channels[J].The Institution of Engineering and Technology, 2012, 6(1): 84–89. |
| [6] | Niedzwiecki M, Cisowski, K. Adaptive scheme for elimination of broadband noise and impulsive disturbances from AR and ARMA signals[J].IEEE Trans Signal Process, 1996, 44(3): 528–537. doi: 10.1109/78.489026 |


