2. 北京邮电大学 计算机学院, 北京 100876
协作干扰策略是实现物理层安全的一种重要方案.但是由于协作节点的能源有限性以及自私性,干扰服务不能无偿提供,为了使得源节点和协作节点之间取得最优的效益分配,提出了一种基于Stackelberg博弈的能效最优报偿及功率分配方案.根据所建立的双层博弈模型,证明了系统存在唯一的全局最优能效,并且给出了最优功率分配方案的闭式解.仿真结果表明,所设计的协作策略在能效方面优于平均功率分配策略,而且所提方案在多节点协作时能取得更优的表现.
2. School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
The secrecy rate of the source-destination link can be effectively improved with help of friendly jammers, but the jamming service is not free. Obviously, there exists a tradeoff between the friendly jammer and the source-destination pair. An optimal power allocation algorithm based on Stackelberg game was proposed. Based on the proposed two-level Stackelberg game model, the existence of unique globally optimal energy efficiency was proved, and the closed-form result of the optimal energy efficiency was derived. Simulations show that the proposed collaboration strategy is better than the average power allocation strategy in terms of energy efficiency. And multi-nodes collaboration could achieve better performance.
物理层安全技术利用无线信道的随机性、时变性及互异性等特征可以保证合法通信的双方在有窃听者存在的情况下进行安全通信而不被窃听到任何信息[1].当合法用户对之间的信道质量差于窃听信道时,无法得到有效的安全传输速率.因此协作干扰机制被提出[2-3],通过利用人工干扰的手段降低窃听信道的质量,从而破坏窃听节点的侦听能力.考虑到协作节点的自私性,提出利用博弈的方法来进行有偿协作的方案[4-5].
Han Z和Zhang等[4-5]分别分析了2个协作干扰节点共同协助时的系统博弈性能及多用户共享单一协作干扰节点系统的博弈性能.针对协作节点能源有限以及合法通信用户间通信质量要求较高的场景,需要多个协作节点进行干扰服务,为了合理分配报偿以及提高协作节点的能效,提出一种基于Stackelberg博弈的能效最优功率分配方案.该方案采用双层博弈策略,第1层博弈确定出最优支付报偿,第2层博弈进行协作节点间的报偿分配和功率调整.
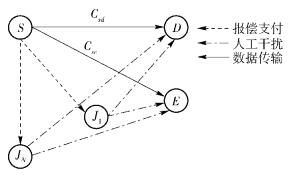
1 系统模型如图 1所示,所考虑的系统包含1个源节点S、1个目的节点D、1个窃听节点E及N个协作干扰节点Ji(i∈N,N={1, 2, …, n}).这里所提到的节点均采用单天线且工作于半双工的模式.窃听节点始终窃听源节点所发送的信息.当源节点到窃听节点间的窃听信道质量弱于主信道质量时,合法通信的双方可以实现物理层安全通信.从源节点到目的节点所能达到的最大安全传输速率称为安全容量,而安全速率则是低于安全容量的可行速率.当主信道质量弱于窃听信道时,为了保证传输信息的安全性,需要诉诸于干扰节点的协助,通过干扰节点发送人工干扰信号以破坏窃听信道的质量,从而营造出可以进行安全通信的环境.
|
图 1 多节点协作干扰模型 |
针对干扰节点协作的通信场景,整个通信过程包括2部分:一是源节点以功率Ps将信号发送给目的节点,同时该信息也将被窃听节点所窃听,此时链路S→D和S→E上的信道增益分别为Gsd和Gse;二是干扰节点Ji以功率Pi对外发送人工干扰信号,此时链路Ji→D和Ji→E的信道增益分别为Gid和Gie.这里假设源节点可以获得每条通信信道的瞬时信道信息,而且每条信道均服从平坦准静态瑞利衰落,在路损模型中,路损系数设定为α,窃听节点及目的节点的热噪声功率表示为σ2.
针对协作节点能源有限及合法通信用户间信道质量较差的场景,为了保证合法通信用户间的安全通信质量,需要多个协作干扰节点进行联合干扰,此时目的节点和窃听节点所能获得的信道容量分别为Csd和Cse:
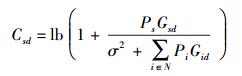
|
(1) |
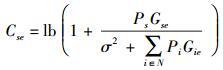
|
(2) |
为了保证源节点所发送数据不被窃听节点所截获,源节点应该以Cs的安全容量进行数据传输,则

|
(3) |
可以看出,由于受到协作节点的影响,Csd和Cse都被相应地降低,如何选择干扰节点以及分配干扰节点的功率将最终影响所取得Cs的效果.
2 物理层安全的协作博弈为了激励更多的节点参与协作以满足合法用户的安全通信需求,同时确保报偿以及所用功率在众协作节点之间进行高效的分配,博弈的思想被采纳.源节点与协作节点之间的博弈关系可以定义为主从式的博弈关系,因此Stackelberg博弈被采用.
2.1 博弈定义在所设计的博弈场景中,源节点S期望通过从多个协作节点Ji处购买到的干扰“服务”来优化自己的安全容量,因此其效用函数Us可表示为
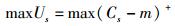
|
(4) |
其中m为源节点付给所有协作干扰节点的总报偿.
协作干扰节点集中的每个协作干扰节点Ji负责为有需求的源节点提供有偿的干扰服务,其通过从源节点处索取报偿以获得利益,因此其效用函数Ui为其所获得报偿与所付出代价之间的差值,即
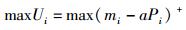
|
(5) |
其中:a为每单位功率所对应的增益;mi为协作干扰节点Ji所获得的报偿,其取决于该节点对于提高主信道安全容量的贡献,则
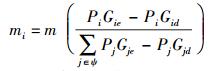
|
(6) |
其中:域ψ为所有参与协作干扰的节点集合,Pj为域ψ中每个协作干扰节点所采用的干扰功率.
由式(4) 和式(5) 可以发现,只有当源节点及协作节点能从该博弈过程中获利时,双方才愿意参与该博弈过程.利用Stackelberg博弈方法进行博弈策略的设计及优化,故源节点即为博弈过程中的购买者,而协作节点则为博弈过程中的拍卖者.
2.2 源节点端的效益分析源节点端作为购买者其目标是从协作节点处以最优的价格购买到尽可能多的干扰服务来提高其所期望的安全容量,因此其效用函数具体可以表示为
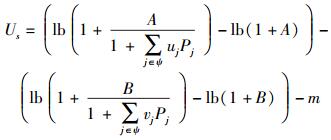
|
(7) |
其中
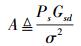
|
(8) |
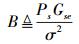
|
(9) |
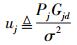
|
(10) |
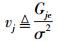
|
(11) |
假设Pj=ρjm,则对于式(7) 来说,当协作节点固定时其所获得的效益与付出的总报偿有关.式(7) 针对m求偏导可得
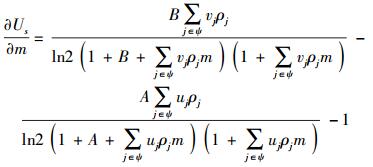
|
(12) |
根据文献[4]中的分析,式(12) 的求解为闭式解,其求解过程过于复杂,为了降低系统复杂度,将系统模型简化:对干扰信号进行预处理,使得干扰信号只对窃听节点造成影响而不会降低目的节点的信道质量.源节点处的效用函数变为
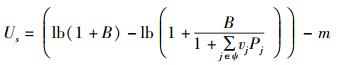
|
(13) |
对于源节点来说,只有当式(13) 关于m的偏导等于0时,其所获得的效益最大,即
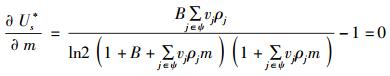
|
(14) |
重新排列式(14) 可以得到
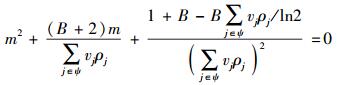
|
(15) |
因此对于式(15) 的闭式解为
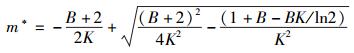
|
(16) |
其中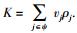
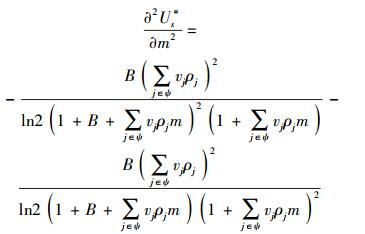
|
(17) |
根据式(17) 可知,Us关于m的二阶导数是小于0的,是关于m的凸函数.故使得Us的一阶导数等于0的m值即为在协作节点功率Pj固定的情况下,使得源节点取得最大效益的点.
2.3 协作节点端的效益分析根据式(5) 和式(6) 可以发现,协作节点所能获取的报偿多少与其所付出的功率及源节点所给出的总报偿有关,其效用函数具体可以表示为
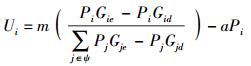
|
(18) |
为了达到所付出的功率与所获得报偿之间的最优配比,假设在总报偿m一定的情况下,求Ui与Pi之间的关系.对式(18) 求Pi的偏导可得
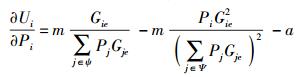
|
(19) |
当式(19) 等于0时,可以求得在系统总报偿m固定的情况下,令协作节点取得最优效益时的功率,即
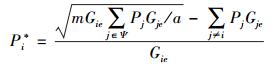
|
(20) |
定理 当参与协作干扰的节点数大于2时,整个博弈过程存在纳什均衡.
证明 根据纳什均衡的定义,为了达到纳什均衡,每个协作干扰节点Ji都选择其最优的干扰功率作为响应,否则将会有干扰协作节点期望调整其策略以获得更好的收益.
因此,对式(20) 进行变形可以得到
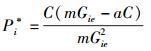
|
(21) |
其中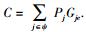
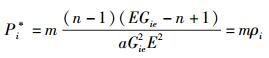
|
(22) |
其中:
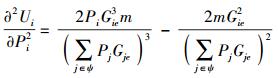
|
(23) |
由式(23) 可以发现,Ui关于Pi的二阶导数小于0,因此Ui是关于Pi的凸函数.又由式(22) 可以发现,只有当
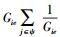
根据文献[6]中的证明,当最优响应函数为正值单调可扩展时,博弈过程的纳什均衡存在且唯一.显然,由式(20) 和式(22) 可以很容易证明Pi*符合以上要求,因此该博弈过程存在唯一的纳什均衡.
3 仿真分析为验证所提的基于Stackelberg双重博弈的性能,将本算法与平均功率分配策略进行对比.考虑通信场景为一个150×150的区域,其中的源节点、目的节点及窃听节点的位置分别位于(0, 0)、(0, 100)、(50, 50),所讨论的协作干扰节点数如表 1所示.为简单起见,所选择的协作干扰节点均在窃听节点附近,进而使得所产生的干扰信号对目的节点的影响很小,甚至在计算过程中可以忽略不计.仿真过程中所需的其他参数如表 1所示.根据式(5) 可知,每单位功率所对应的增益a对于系统所计算的最优功率及系统效益有着至关重要的影响,因此在仿真过程中,a的取值从100~1 000进行动态变化,以分析不同的a对于系统性能的影响.
|
|
表 1 协作干扰系统参数 |
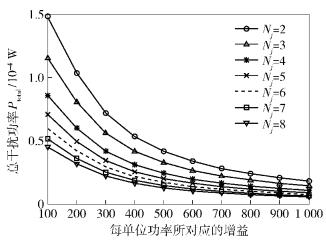
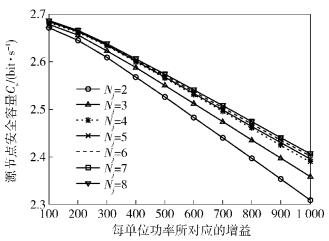
如图 2所示,无论是在N=2或者N=8时,所设计的策略能取得更高的安全容量与总干扰功耗(Ptotal)比,即所提出的方案可以消耗更少的功耗而实现同样的安全容量提升效果. 图 3和图 4分别展示了所设计的Stackelberg博弈策略对应于不同协作干扰节点参与时,平均每个协作节点所需消耗的干扰功率及源节点所能获得的最大安全容量.从整体平均的角度来看,当有多个节点进行协作时,每个协作干扰节点可以采用较小的功率即可使源节点获得较高的安全容量.

|
图 2 Stackelberg博弈策略与均匀分配策略的对比 |
|
图 3 不同协作干扰节点参与情况下的总干扰功率对比 |
|
图 4 不同协作干扰节点参与时,源节点所能获得的最大安全容量 |
由于各节点距离窃听节点位置的不同,其干扰信号对窃听节点的影响也不同,所以从图 5中可以明显发现,在有8个节点进行同时协作干扰时,利用Stackelberg博弈,不同节点间对于所得报偿进行的博弈竞争,促使各节点采用最合理的功率进行协作,从而实现如图 4中所示的源节点处的最优安全容量.

|
图 5 N=8时,每个协作干扰节点的功率分配 |
针对协作干扰节点的自私性,提出了一种基于Stackelberg博弈的协作激励策略.根据所建立的双层博弈模型,在有效激励协作干扰节点进行参与的同时,实现了多节点间的功率最优分配.仿真结果表明,所设计的协作策略在能效方面优于平均功率分配策略,而且在多节点协作时,所取得的单节点能效及源节点所获得的安全容量均优于少数节点协作时的表现.
| [1] | Wyner A D. The wire-tap channel[J].Bell System Technical Journal, 1975, 54(8): 1355–1387. doi: 10.1002/bltj.1975.54.issue-8 |
| [2] | Dong Lun, Yousefi'zadeh H, Jafarkhani H. Cooperative jamming and power allocation for wireless relay networks in presence of eavesdropper[C]//IEEE International Conference on Communications (ICC). Kyoto:[s.n.], 2011: 1-5. |
| [3] | Gabry I F, Thobaben R, Skoglund M. Outage performance for amplify-and-forward, decode-and-forward and cooperative jamming strategies for the wiretap channel[C]//IEEE Wireless Communications and Networking Conference (WCNC). Cancun:[s.n.], 2011: 1328-1333. |
| [4] | Han Z, Marina N, Debbah M, et al. Physical layer security game: how to date a girl with her boyfriend on the same table[C]//International Conference on Game Theory for Networks. Istanbul:[s.n.], 2009: 287-294. |
| [5] | Zhang Rongqing, Song Lingyang, Han Zhu. Improve physical layer security in cooperativ wireless network using distributed auction game[C]//2011 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS). Shanghai:[s.n.], 2011: 18-23. |
| [6] | Yates R. A framework for uplink power control in cellular radio systems[J].IEEE Journal on Selected Areas in Communications, 1995, 13(7): 1341–1347. doi: 10.1109/49.414651 |



