基于修正的Carreau本构方程,推导出了考虑剪切稀化非牛顿流变特性的雷诺方程,利用新型高压流变仪对PAO650流动曲线进行了测试,得到了聚α-烯烃(PAO)650的流变参数值;通过理论和实验研究了PAO650的弹流润滑(EHL)成膜特性.研究结果表明,基于剪切稀化弹流的理论研究结果与实测值吻合较好,剪切稀化非牛顿流变效应使PAO650发生严重油膜稀化现象,经典弹流油膜厚度公式中的卷吸速度指数需要调整,滑滚比对PAO650的成膜特性影响不大.
Based on modified Carreau constitutive equation, the Reynolds equation was deduced, which considers shear-thinning non-Newtonian property. The flow curve of poly alpha olefin (PAO)650 was measured with high-pressure rheometer. The rheological parameters were obtained by fitting the related test data. PAO650 elastohydrodynamic lubrication (EHL) film forming properties were studied. Experiment indicates that PAO650 film forming properties based on shear-thinning EHL theory very well agree with the experimental results. The shear-thinning non-Newtonian rheological effect makes PAO650 film-thinning severely. For PAO650, the entrainment rate index of classic EHL film thickness formula needs to be adjusted. The slide-roll ratio has little impact on PAO650 film-forming properties.
聚α-烯烃(PAO, poly alpha olefin)基础油以其优越的性能被认为是最具发展潜力的润滑油,广泛应用于航空航天、液压以及雷达电子等精密装备中.但是,目前对PAO的研究主要集中在其合成和摩擦磨损特性方面,而对其成膜能力的研究一直以来鲜有报道.
笔者以美孚公司生产的PAO650为研究对象,试验确定了描述其流动曲线的本构方程及其流变参数;试验测试了不同压力下PAO650的粘度值,确定了其粘度方程;理论分析了PAO650在不同工况下的成膜特性,用纳米级油膜厚度测量仪对PAO650成膜特性进行了试验研究;最后将理论分析结果与实验研究结果进行了对比.本研究对揭示PAO650的弹流成膜特性及其合成具有重要的理论意义和实际应用价值.
1 数学模型1.1 剪切稀化流变模型采用修正Carreau本构方程描述PAO650的表观粘度η与剪应力τ之间的关系.研究表明,修正Carreau本构方程能较好地描述弹流工况下润滑油的剪切稀化非牛顿流变特性[1]:
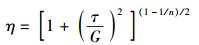
|
(1) |
其中:η为表观粘度,τ为油膜剪应力,G为牛顿极限剪应力,n为幂指数.为了便于理论计算,将式(1) 变为
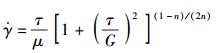
|
(2) |
其中: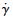
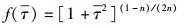
|
(3) |
其中:τ=τ/G.将式(3) 代入式(2),得式(2) 的量纲为一的形式为
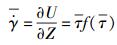
|
(4) |
其中:U为量纲为一的卷吸速度,U=uμ/(hG),u=(u1+u2)/2,u1和u2分别为上下表面的滚动速度;Z=z/h,z为油膜厚度方向坐标,h为油膜厚度.
1.2 广义雷诺方程忽略惯性力和油膜压力沿z方向的变化,单位油膜运动方程为
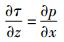
|
(5) |
其中x为滚动方向坐标.将式(5) 沿z方向积分,得量纲为一的剪应力为

|
(6) |
其中:τa为z=0处的剪应力,p为油膜压力.引入下列边界条件:
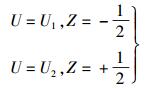
|
(7) |
其中:U1=u1μ/(hG),U2=u2μ/(hG).积分式(4) 得
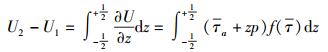
|
(8) |
x方向的流量为
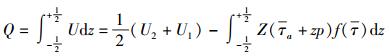
|
(9) |
质量连续方程为
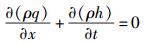
|
(10) |
其中:ρ润滑油密度,t为油膜被剪切时间,
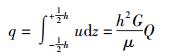
|
(11) |
将式(9) 代入式(11),式(10) 变成
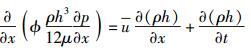
|
(12) |
其中
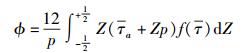
|
式(12) 为广义雷诺方程,与经典弹流雷诺方程相比,唯一的不同之处是引进了参数ϕ.若ϕ=1,则式(12) 为经典弹流雷诺方程.仅考虑稳态工况,式(12) 的量纲为一的形式为
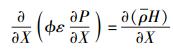
|
(13) |
其中: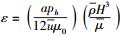
油膜厚度量纲为一的方程为
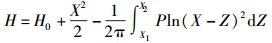
|
(14) |
其中:H=h/a;H0=h0/a,h0为无载荷中心油膜厚度.
载荷平衡量纲为一的方程为
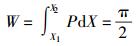
|
(15) |
Doolittle-Tail自由体积粘度方程[2]为
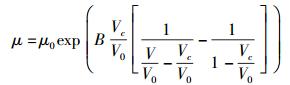
|
(16) |
其中:V为体积;V0为气压下润滑油体积;Vc和B为待定常数,在一定条件下,不同的润滑油,参数Vc和B不同. Tait方程[3]描述润滑油体积与压力的关系为
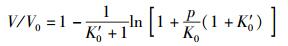
|
(17) |
其中:K0和K′0为待定常数.油膜的密压方程为式(17) 的倒数.
采用多重网格法求解式(13)~式(17) 组成的非线性定解方程组,可得油膜厚度分布和压力分布.
2 试验部分2.1 试验材料及设备高压Couette流变仪用于测试PAO650的流动曲线,该流变仪是一种可调压的同心圆筒流变仪,可测试的剪切率工况大于105/s,具体结构及工作原理见文献[4];Brookfield DV-Ⅲ粘度计对PAO650的低剪切粘度进行测量;采用纳米级膜厚测量仪测试不同工况下PAO650的弹流油膜厚度,该油膜厚度测试仪主要由显微镜、CCD、图像采集卡、计算机和冷光源等组成[5].试验中,钢球的直径为21 mm,载荷为32 N,钢球与玻璃盘的综合弹性模量为123.9 GPa,Hertz最大压力为ph=0.53 GPa;钢球和玻璃盘表面综合粗糙度值小于5 nm,接触区域的温度由外部的温控系统控制,保证达到所需温度.
2.2 试验结果图 1所示为在压力为50 MPa,温度为20 ℃工况下,PAO650相对粘度η/μ随剪应力τ的变化曲线.图中虚线为式(1) 给出的流动曲线.基于式(1),用最小二乘法拟合试验数据,得到PAO650的流变参数为n=0.74、G=31 kPa,其误差和均方误差分别为0.450和0.502 833 11. 图 1表明,修正Carreau本构方程较好地描述了PAO650的流动曲线.

|
图 1 PAO650相对粘度随剪应力变化曲线 |
表 1所示为在不同压力与温度工况下,由Brookfield粘度计测量得到的PAO650粘度值,剪切应力τ的范围为33~65 Pa.
|
|
表 1 PAO650粘度值 |
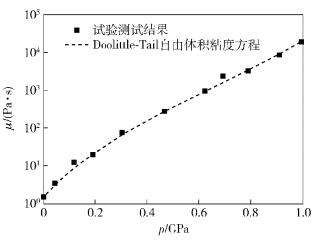
图 2所示为温度在75 ℃时,PAO650粘度随压力变化的曲线.图中虚线为Doolittle-Tail自由体积粘度方程给出的曲线,可以看出,该方程与实验数据吻合得较好.基于式(16),拟合表 1中的试验数据,得PAO650粘度方程中的参数为V0=0.669 4、B=4.422、K′0=12.82、K0=1.425 2 GPa、μ0=1.42 Pa·s.
|
图 2 PAO650粘度随压力变化曲线 |
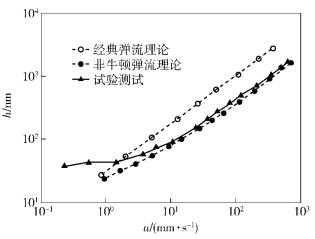
图 3所示为纯滚动工况下PAO650中心膜厚随卷吸速度变化的情况.工况条件为:Hertz最大压力为0.5 GPa,温度为75 ℃.同时,图 3也给出了基于经典弹流理论的结果.结果表明,当卷吸速度u高于28 mm/s时,理论计算值与试验测试结果基本一致,从图 3中可以看出,在此种工况下PAO650的润滑状态为EHL;当卷吸速度u低于28 mm/s时,实测膜厚明显高于理论计算值,此时PAO650的润滑状态为薄膜润滑,应用薄膜润滑理论进行分析,EHL理论不再适用. 图 3还表明,经典弹流理论预测值远远大于理论分析值和试验测试值,因此经典EHL理论不能准确预测PAO650的油膜厚度,卷吸速度越大,其误差越大.
|
图 3 PAO650的中心膜厚随卷吸速度变化曲线 |
基于方程ln(h)=a+bln(u),对理论分析膜厚值进行线性回归,回归结果b=0.599.温诗铸和杨沛然[6]提出的基于经典EHL理论回归线接触弹流中心膜厚公式为
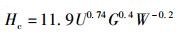
|
(18) |
其中,对应的b=0.74,与b=0.599差别较大,表明PAO650在弹流工况下发生了严重的剪切稀化,没有考虑剪切稀化效应的经典弹流理论预测的膜厚值远大于实测值.实验结果显示,当滚动速度较高时,经典弹流理论给出的膜厚为实测膜厚的2倍,因此理论分析PAO650的成膜特性时,必须考虑其剪切稀化效应.
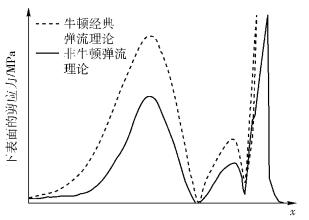
图 4所示为滚动速度为0.2 m/s时,基于经典弹流理论和剪切稀化非牛顿弹流理论,下润滑表面上的剪应力沿x方向分布情况. EHL油膜厚度是由入口区域油膜特性决定的,因此,这里只考虑x<0的情况. 图 4表明,在2种理论下油膜压力梯度几乎相同,在纯滚动工况下,油膜内的剪应力为τ(x)=(h/2)(dp/dx),由于经典弹流理论没有考虑剪切稀化效应,所以剪应力值较高,由式(18) 可知,对应的油膜厚度也较高;由于考虑剪切稀化非牛顿弹流理论润滑油的剪切稀化效应,油膜剪应力值相对较小,所以油膜出现稀化现象,这与图 3的结果相吻合.
|
图 4 油膜内剪应力沿x方向的分布情况 |
图 5所示为滚动速度为0.15 m/s时弹流中心膜厚随滑滚比S的变化情况. 图 5表明,滑滚比对膜厚的影响不大,当滑滚比从S=0.0的纯滚动工况到S=0.5的滑动工况时,弹流中心膜厚仅仅降低了约3.8%. 图 5同时给出了经典弹流理论预测的膜厚值,剪切稀化非牛顿弹流理论给出的结果与实测结果非常吻合.

|
图 5 弹流中心膜厚随滑滚比的变化关系 |
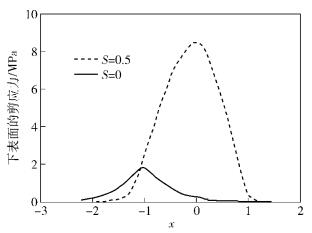
图 6所示为滚动速度为0.2 m/s时,在2种滑滚比S=0.0和S=0.5工况下,下润滑表面上的剪应力沿x方向分布情况.从图 6中可以看出,在赫兹接触区域,滑滚比S=0.0工况下的剪应力大大低于滑滚比S=0.5时的剪应力,而在该2种工况下入口区的剪应力却相差不大.由于弹流油膜稀化主要由入口区域油膜特性决定,所以图 6显示的结果与图 5显示的结果极为吻合.
|
图 6 不同滑滚比工况下油膜剪应力分布 |
1) 对于PAO650,在所分析的工况范围内,当卷吸速度u大于28 mm/s时,其润滑状态为弹性流体动力润滑;当卷吸速度u小于28 mm/s时,其润滑状态为薄膜润滑.
2) 剪切稀化非牛顿流变弹流理论能较精确预测PAO650的弹流油膜厚度,而经典EHL理论过高估计了PAO650的膜厚值.对于PAO650,应该将经典弹流油膜厚度公式中的速度指数由0.74调整为0.599.
3) 滑滚比S对PAO650的弹流成膜特性影响不大.因此,在对其油膜厚度进行理论预测时,可以忽略滑滚比S的影响.
| [1] | Habchi W, Bair S, Qureshi F, et al. A film thickness correction formula for double-Newtonian shear-thinning in rolling EHL circular contacts[J].Tribology Letter, 2013, 50(1): 59–66. doi: 10.1007/s11249-012-0078-6 |
| [2] | Liu Yuchuan, Wang Q Jane, Bair S, et al. A quantitative solution for the full shear-thinning EHL point contact problem including traction[J].Tribology Letter, 2007, 28(2): 171–181. doi: 10.1007/s11249-007-9262-5 |
| [3] | Jang J Y, Khonsari M M. Correction factor formula to predict the central and minimum film thickness for shear-thinning fluids in EHL[J].Journal of Tribology, 2008, 130(02): 4501–4504. |
| [4] |
郭关柱, 范毓润, 杨华勇. 一种新的Couette流变仪的精度校核[J]. 机械工程学报, 2009, 45(6): 147–153.
Guo Guanzhu, Fan Yurun, Yang Huayong. Accuracy verification of a new couette rheometer[J].Journal of Mechanical Engineering, 2009, 45(6): 147–153. |
| [5] | Naughton J W, Hind M D. Multi-image oil-film interferometry skin friction measurements[J].Measurement Science and Technology, 2013, 24(12): 3–14. |
| [6] | 温诗铸, 杨沛然. 弹性流体动力润滑[M]. 北京: 清华大学出版社, 1993: 1-377. |



