提出了一种基于改进Kruskal算法的无线传感器网络(WSN)故障节点检测方法.该方法首先通过集中式的改进Kruskal最小生成树算法来获取可信的节点集合,之后依据可信节点,采用邻居节点比较算法对传感器节点的感知值进行分布式分析和处理,判定发生故障的传感器节点.同时为了容忍节点的临时故障,引入了时间冗余.仿真结果表明,在节点故障率高达35%时,该方法依然能快速定位故障节点,并且同时保证很高的检测精确度.
A fault detection method for wireless sensor network based on improved Kruskal algorithm was proposed. It adopts the centralized improved Kruskal algorithm to obtain credible node set. According to the credible node, it uses the distributed adjacent node comparing algorithm to locate the fault wireless sensor network node by analyzing and processing the sensing value. Time redundancy is also employed for tolerating the transient faults in sensing and communication. Simulation shows that, even the fault note rate raises to 35%, the proposed method can still locate the fault node quickly, and can also guarantee a high accuracy.
近年来,无线传感器网络(WSN,wireless sensor networks)作为一种新兴的网络技术被学术界和工业界所关注和研究.由于WSN节点通常部署在不可控的、复杂的环境中,网络节点非常容易发生故障,这严重影响了WSN的运行质量[1].
在WSN节点故障检测的相关研究中,Krishnamachari等[1]和Luo Xuanwen等[2]基于贝叶斯故障识别算法来进行故障检测. Liu Kebin等[3]主要研究了节点故障检测过程中的能量节省问题. Lee等[4]联合时间相关性和空间相关性来诊断传感器节点故障,并通过时间冗余机制来实现对临时故障的容忍. Tsang等[5]提出了一种CSFD机制来检测网络中的故障节点. Banerjee等[6]提出了一种多项式模式下通过传感器节点的聚合树来实现区域内的事件感知方法. Yim等[7]引入节点信誉,基于最大生成树,采用分簇的结构提出了一种故障事件检测算法.然而,以上文献提出的方法在故障节点比例较高、需要快速定位时效率较低,所需计算量较大,并且检测精度也相对较低.针对以上问题,笔者提出了一种基于改进Kruskal算法的WSN故障节点检测方法.该方法综合了集中式与分布式检测方法的特点,通过集中式的Kruskal算法和分布式的邻居节点比较方法,定位发生故障的传感器节点,从而为快速恢复网络性能提供必要的依据.
1 WSN模型描述由于WSN节点能量有限,因此针对WSN的故障检测方法通常采用分布式结构. Yim等[7]提出了一种分簇方法,通过汇集节点维护簇表,使得簇内任意节点通过交换数据能获取到其他节点的感知数据.笔者将在其基础上讨论簇内节点检测方法的实现.
为了有效分析,每次故障检测算法执行之前,剩余能量最高的节点将被选为簇头节点.簇头节点负责执行故障检测算法.设簇内的节点随机分布并且具有相同的传播距离s,每个节点缓存自身前m个时刻的感知数据并且能接收并缓存其邻居节点的前m个时刻的感知数据.同时,假设区域内的节点可用性始终维持在50%以上,且区域内数据的空间特征均匀分布.基于这些分析,将进一步研究集中式的可信节点获取算法和分布式的故障节点检测方法.
2 可信节点获取算法首先介绍WSN的带权图表示方式和节点权值的计算方式,然后介绍Kruskal最小生成树生成方法以及用于故障检测的IKruskal(imporved Kruskal)可信节点集获取算法.为了方便分析,表 1给出了主要参数.
|
|
表 1 主要参数表 |
为了方便描述传感器节点与其邻居节点的关系,针对WSN构建一个无向带权图G(D)=(V, E),其中,点集V={vi|vi∈D}中的元素表示传感器节点,每个点vi={di1, di2, …, dim}具有m个属性,分别代表相应无线传感器节点每个时刻的感知数据;边集E={eij|vi, vj∈D, i≠j}包含不同传感器节点感知数据之间的关系,每条边eij具有权值wij,其中权值wij采用欧氏距离度量方式,即

|
(1) |
Kruskal算法是求解最小生成树的经典算法,它的特点是通过选择图G(D)中权值最小的边来获取最小生成树T.
设簇头节点在每次检测前通过信息交换收集簇内节点前m个时刻的感知数据,针对图G(D)=(V, E)运用IKruskal算法来获取相对可信的传感器节点集合.在求解最小生成树T=(VT, ET)时,统计子树所包含的节点数|VT|,若满足|VT|/n≥α,停止求解过程,并设该子树所有节点为可信节点,改进的算法描述如算法1所示.
算法1 Ikruskal算法
步骤1 簇头节点收集簇内节点信息,初始化时令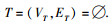
步骤2 簇头节点将所有的边eij∈E依权重wij递增排序.
步骤3 while 
按序取eij∈E,if eij∉ET,then
ET=ET∪{eij};VT=VT∪{vi, vj};
if T是生成树and |VT|/n≥α,then
保存T,return;
end if
end if
E=E-{eij};end while
步骤4 得到可信节点集VT.
通过IKruskal算法获取的可信节点集合由参数α来确定.进一步,针对网络中的其他节点,通过与可信节点的相关性对比分析来检测网络中的故障节点.与Kruskal算法相近,IKruskal的时间复杂度也为O(|E|×lg(|E|)).
3 故障节点检测方法簇头节点通过IKruskal算法获取可信节点集合并将结果VT扩散到簇内. VT内节点将会采用分布式的方法,以获取的可信节点为参考,根据邻居节点比较算法[5]来判断其邻居节点的状态,最后簇头节点会统计所有簇内节点的状态.具体的工作流程描述如下.
首先,假设用布尔变量Fi表示节点vi的工作状态,0和1分别表示正常和故障状态,则对于可信节点集合VT中的节点,其Fi取值均为0.
根据相邻节点的测量值具有空间相关性这个特点,对给定的2个相邻节点vi和vj,定义
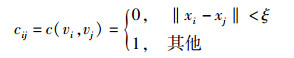
|
(2) |
其中阈值ξ是一个经验数据,它的取值与传感器网络的应用场景相关.
为了避免偶然性故障,引入了时间冗余机制[4],定义ck(vi, vj)为vi与vj在k时刻的比较函数.
对于节点vi与其所有邻居节点在不同时刻的比较结果,可以用一个r×m的矩阵Ci表示,即

|
(3) |
这样,vi和其邻居节点vj的时间域上的相似值c′ij可以用矩阵中的第j行表示,即
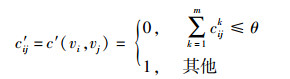
|
(4) |
其中θ为预定的阈值,表示对节点偶然性故障的容忍程度.
基于IKruskal算法获取可信节点集VT,运用VT中节点对其他剩余节点进行故障检测并修正VT中误差节点状态,具体检测步骤如算法2所示.
算法2 故障节点检测算法
步骤1 簇头节点获取相对可信节点集VT,对任意vi∈VT,if 
步骤2 簇内节点根据节点集VT初始化Fi=0,若vi∈VT,生成其邻居节点集合N(vi),初始化Fi=0;生成矩阵Ci,初始化cijk=1;若vi∉T,初始化Fi=1.
步骤3 若vi∈VT,对vi执行如下过程.
for vj∈N(vi),k=1, 2, …, m
if ‖xik-xjk‖ < ξ then cijk=0;end if
for vj∈N(vi)
if 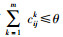
if c′ij=0 and Fi=0,then
Fj=0;VT=VT∪{vj};
生成N(vj),生成矩阵Cj;end if
if c′ij=1 and Fi=0 and Fj=0,then
Fj=1;将vj标记为故障节点
end if
对VT中所有的节点vi重复执行步骤3.
步骤4 VT中节点扩散邻居节点的状态信息F,簇头节点收集并根据这些信息统计所有簇内节点的状态信息.
算法2首先从时间关联性上进一步分析节点的可信性.当时间域上节点间的差异大于指定值γ时,可以将其从可信节点集合中删去.以可信节点集为中心的相邻节点的状态判断,则以数据的空间相关性累计值作为依据.算法2的时间复杂度为O(|VT|2+m|VT|N(VT)),属于多项式的时间域,复杂度较低.
4 仿真结果和分析下面通过Matlab对提出方法进行仿真,并对其性能进行分析.通过与以往已存在的检测算法对比,分析在不同的节点下,故障诊断精度(CDR, correct detection rate)和虚警率(FAR, false alarm rate)[2]的变化.文中ξ取1,γ取1.
在仿真实验中,假设α=0.45, m=8,并且每个时刻正常节点发生偶然性故障的概率为pf=0.1,故障节点出现正常感知值的概率为pg=0.05.为了更好地验证提出方法的性能,假设节点总数分别为40、60、80和100,并且随机分布在100×100的区域内,针对不同的节点总数n,假设故障节点的比例p分别为0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40和0.45.文中感知的数据值为温度,单位为℃.相邻节点的判断通过距离s来确定,取s=10 m.
图 1所示为故障节点比例p=0.3时,通过IKruskal方法获取可信节点集后的节点分布,其中“+”表示可信节点.可信节点随机分布在感知区域内,可以用来检测其他节点的工作状态.
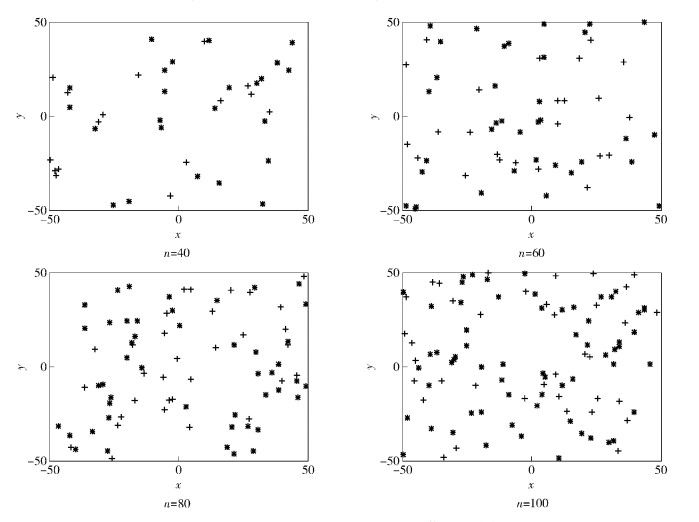
|
图 1 p=0.3时经过IKruskal选取的可信节点分布 |
图 2所示为当n=60,并且θ分别为1、2、3时的CDR和FAR对比.在时间冗余度固定时,CDR和FAR均与θ成反比,也就是说,若θ取值越小,虽然CDR有提高,但是相应的FAR也较高.在后续的仿真中,折中选择θ=2.
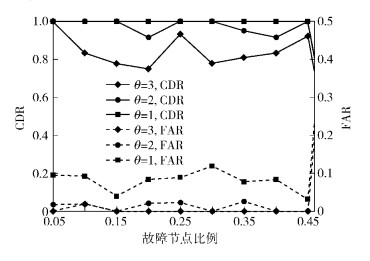
|
图 2 n=60时,CDR/FAR与θ的关系 |
图 3所示为同一次仿真中的CDR和FAR.可以看出,随着节点总数的增加,算法的性能更加趋于平稳,相应的CDR和FAR也更加精确,并且,当故障节点比例p增加到35%时,算法依然能保证很高的检测精度.
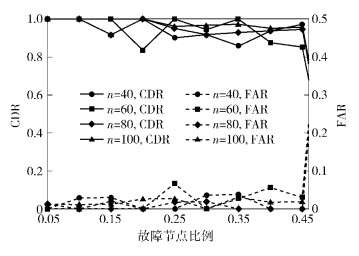
|
图 3 θ=2时,CDR/FAR随n的变化 |
图 4所示为所提算法与Bayesian算法[2]的对比.所提出的算法相对于Bayesian算法随故障节点比例的增加,能保证更佳的CDR和FAR.当故障节点比例小于40%时,提出的算法能保证很稳定的性能,但是Bayesian算法的检测性能急剧下降.
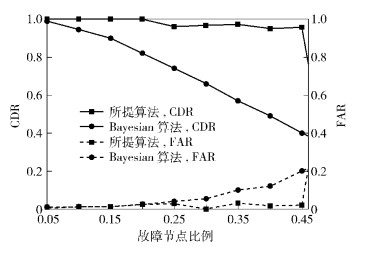
|
图 4 算法性能对比 |
提出了一种基于改进的Kruskal最小生成树求解方法的WSN故障检测方法.仿真结果显示,当检测区域内故障节点比例增至35%时,该方法依然能快速地检测故障节点并保证很高的检测精度.而且,通过与以往的检测方法对比,该方法在节点故障增加时依然能保证稳定的检测性能和检测精度.下一步的工作是在区域检测数据不均匀的状态下,研究更加有效的传感器故障节点检测方法.
| [1] | Krishnamachari B, Iyengar S. Distributed bayesian algo-rithms for fault-tolerant event region detection in wireless sensor networks[J].IEEE Transactions on Computers, 2004, 53(3): 241–250. doi: 10.1109/TC.2004.1261832 |
| [2] | Luo Xuanwen, Dong Ming, Huang Yinlun, et al. On distributed fault-tolerant detection in wireless sensor networks[J].IEEE Transactions on Computers, 2006, 55(1): 58–70. doi: 10.1109/TC.2006.13 |
| [3] | Liu Kebin, Ma Qiang, Zhao Xibin, et al.Self-diagnosis for large scale wireless sensor networks[C]//INFOCOM 2011.Shanghai:2011 Proceedings IEEE, 2011:1539-1547. |
| [4] | Lee M H, Choi Y H. Fault detection of wireless sensor networks[J].Computer Communications, 2008, 31(14): 3469–3475. doi: 10.1016/j.comcom.2008.06.014 |
| [5] | Wang Tsangyi, Chang Liyuan, Chen Peiyin, et al. A collaborative sensor-fault detection scheme for robust distributed estimation in sensor networks[J].IEEE Transactions on Communications, 2009, 57(10): 3045–3058. doi: 10.1109/TCOMM.2009.10.080244 |
| [6] | Banerjee T, Xie Bin, Grawal D P, et al. Fault tolerant multiple event detection in a wireless sensor network[J].Journal of Parallel and Distributed Computing, 2008, 68(9): 1222–1234. doi: 10.1016/j.jpdc.2008.04.009 |
| [7] | Yim S J, Choi Y H. An adaptive fault-tolerant event detection scheme for wireless sensor networks[J].Sensors, 2010, 10(3): 2332–2347. doi: 10.3390/s100302332 |



