2. 西安邮电大学 通信与信息工程学院, 西安 710061
针对每个移动终端进行动态的三维波束赋形,为了使三维波束主瓣对准期望用户并且在干扰用户方向形成零陷,构建了均匀平面阵的二维阵列信号模型,研究了基于最小均方误差算法的全局自适应算法,并在此基础上提出了基于降维的局部自适应算法. 2种自适应三维波束赋形算法可以动态地调整阵列单元的权值,自适应地改变天线阵列的方向图,为用户提供实时的跟踪服务.仿真结果表明,在一定数量的阵列天线单元的条件下,2种算法均可以实现针对期望用户的自适应三维波束赋形.
2. School of Telecommunications and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710061, China
3D-beamforming could use the vertical dimension for antenna pattern adaption, it can provide an additional degree of freedom for transmission signal optimization. A global adaptive 3D-beamforming algorithm based on uniform planar array and a dimension reduction vision algorithm based local adaptive algorithm was proposed. 3D-beamforming algorithm could adjust the antenna weight adaptively according to the user's move or the change of the wireless condition and alter the beam pattern in real time. Simulation shows that the 3D-beamforming aimed at specific user can be implemented by both of the proposed algorithms under a certain number of antenna arrays.
传统二维波束赋形技术中垂直方向的天线下倾角是固定的,只能针对目标用户所在水平方向的一个小型扇区进行波束赋形,不能复用垂直方向的空域资源.三维波束赋形可以对水平和垂直方向的三维空间进行波束赋形,提高了系统能量效率,提升了空域资源的利用率和系统容量[1].
首先构建了均匀平面阵的二维阵列信号模型,然后将自适应波束赋形算法应用于均匀平面阵的三维波束赋形技术,并提出了均匀平面阵基于降维的局部自适应波束赋形改进算法,最后对2种自适应的三维波束赋形算法进行仿真分析.
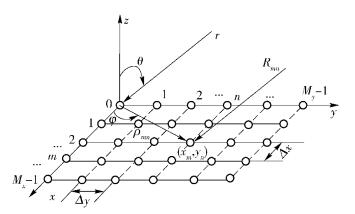
1 二维阵列信号模型常见的二维阵列有均匀圆阵、L形阵列及均匀平面阵等.均匀平面天线阵是指天线单元按行、列等间距排列在一个平面内,若阵列的边界是一个矩形,则为矩形平面阵,如图 1所示.阵列中各天线单元类型相同,尺寸相同,馈电幅度相等,沿x、y方向,天线单元间距分别为Δx、Δy,单元数分别为Mx和My.
|
图 1 均匀平面阵的阵列模型 |
假设一个波长为λ的窄带信号s从(θ, φ)方向平行入射到各个阵元,记(xm, yn)为均匀平面阵中第m行、第n列的阵元,则该阵元接收到的信号与原点处阵元接收到的信号的相位差为

|
(1) |
则在k时刻,均匀平面阵上接收到的信号为

|
(2) |
其中

|
(3) |
沿x和y方向排列的均匀直线阵的相位差分别为

|
(4a) |

|
(4b) |
沿x和y方向排列的均匀直线阵的阵列响应矢量分别为

|
(5a) |

|
(5b) |
根据几何原理易证得
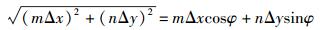
|
(6) |
因此,式(1) 可改写为

|
(7) |
因此,均匀平面阵的阵列响应矢量为

|
(8) |
假设一个期望窄带信号s从(θ0, φ0)方向平行入射到各个阵元,另外有p(p≤MxMy)个干扰信号s1, s2, …, sp分别从(θ1, φ1), (θ2, φ2), …, (θp, φp)方向入射到各个阵元,则在k时刻,均匀平面阵上接收到的信号为

|
(9a) |
或

|
(9b) |
其中n(k)为k时刻的噪声.
2 自适应三维波束赋形算法目前,波束赋形的研究主要集中在基于自适应算法[2]的二维波束赋形及基于波达方向(DoA, direction of arrival)估计的二维波束赋形研究.然而,关于三维波束赋形的研究较少. Saur和Halbauer等[3-4]研究了通过设置几个不同固定下倾角的天线来覆盖整个小区,对不同区域的用户采用不同下倾角的天线来实现三维的波束赋形.通过调整下倾角可以在一定程度上提高系统性能,但是下倾角的调整很缓慢,很难针对移动的目标用户进行连续的波束赋形.
2.1 二维阵列的全局自适应算法假设均匀平面阵接收到的信号为x(k),为了从中提取期望信号s(k),用户首先要发射特定的参考信号(训练序列),接收端根据阵列输出与参考信号d之间的误差e不断地迭代调整w,最终得到使得均方误差最小的阵列单元权值w,并以此作为最优权值处理后续的用户数据.最小均方误差(LMS, least mean square)波束赋形算法原理如图 2所示.

|
图 2 LMS波束赋形算法原理 |
LMS波束赋形算法[5]是基于最陡下降法不断迭代更新的自适应算法,最陡下降法就是沿着代价函数负梯度方向搜索,最终收敛于使代价函数最小的最优解,其权值迭代更新的公式为

|
(10) |
在收敛因子μ已经确定的情况下,为了避免因输入信号x(n)过大,而引起μe*(n)x(n)增大,减慢收敛速度并带来过载噪声,采用归一化最小均方(NLMS,normalized least mean square)算法[6],其权值迭代公式为

|
(11) |
其中收敛因子μ的取值为0和1之间的一个定值. NLMS波束赋形算法控制了权向量的改变,使每次迭代权向量的改变值达到最小,有效地抑制了LMS波束赋形算法所带来的梯度噪声,且收敛速度相比LMS波束赋形算法较快.
基于NLMS的三维波束赋形算法的每次迭代中需要计算均匀平面阵中Mx×My个阵元的权值,本研究称为均匀平面阵的二维阵列全局自适应算法.
2.2 基于降维的局部自适应算法当阵元数目较多时运算量非常大,均匀平面阵的二维阵列全局自适应算法会增加存储及计算复杂度和时延,不利于算法的应用.为此,此处考虑通过降维的方法减少运算量及计算的复杂度,采用基于降维的局部自适应波束赋形算法,即通过分别计算一个Mx阵元和一个My阵元的一维均匀线阵权值来确定均匀平面阵的Mx×My个阵元的权值.
根据MMSE准则,可得均匀平面阵波束赋形的代价函数为

|
(12) |
为了使均方误差最小,则与期望信号无关的部分应该为零.因此,均匀平面阵波束赋形的代价函数结合式(8) 可简化为

|
(13) |
令

|
(14) |
其中

|
(15a) |
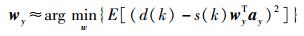
|
(15b) |
为了使均方误差最小,则有

|
(16) |
所以

|
(17) |
由此可以看出,通过分别计算一个Mx阵元和一个My阵元的一维均匀线阵的权值可以来确定均匀平面阵的Mx×My个阵元的权值.
3 仿真结果假设期望信号的入射角度为(30°, 120°),干扰信号的入射角度分别为(60°, 120°)和(45°, 180°),噪声为加性高斯白噪声,信干噪比为20 dB.均匀平面阵x、y方向阵元数分别为Mx=My=8,阵元间距为Δx=Δy=λ/2.分别用二维阵列全局NLMS波束赋形算法和基于降维的局部NLMS波束赋形算法来实现三维波束赋形,对这2种方法的波束赋形效果及收敛速度进行比较.
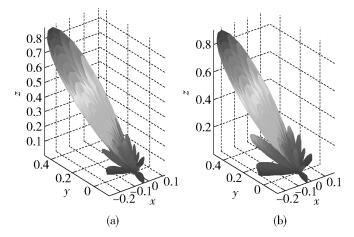
3.1 三维波束图通过二维阵列全局NLMS波束赋形算法和基于降维的局部NLMS波束赋形算法分别得到均匀平面阵各阵元的权值,然后计算出图 3所示的均匀平面阵的三维波束图.
|
图 3 均匀平面阵的三维波束 |
图 3(a)为二维阵列全局NLMS算法得到的三维波束图,图 3(b)为基于降维的局部NLMS算法得到的三维波束图.由图 3可以看出,基于降维的局部NLMS波束赋形算法得到的波束的旁瓣相对较大,这是由于二维阵列全局NLMS波束赋形算法中每个阵元的权值都是相对独立的,可以针对每个阵元处的干扰及噪声状况进行调整,而基于降维的局部NLMS波束赋形算法只是对阵列的一行和一列进行计算,然后求得整个阵列的权值,没有考虑到每个阵元上的干扰和噪声的具体情况.
为了检验以上波束赋形仿真结果中波束指向准确性,以二维阵列全局NLMS波束赋形算法的结果为例,将直角坐标系中的天线方向图映射到水平角、俯仰角及波束幅度组成的空间,仿真结果如图 4所示.

|
图 4 均匀平面阵角度空间方向图 |
图 4(a)为均匀平面阵向(30°, 120°)方向波束赋形的能量在角度空间分布的三维立体图.由图 4(b)可以看出,波束的俯仰角指向30°方向.由图 4(c)可以看出,波束的水平角指向120°方向.由图 4(d)可以看出,波束能量集中在期望信号的(30°, 120°)方向.
3.2 收敛曲线除了运算复杂度和收敛精度外,自适应算法的收敛速度是影响算法性能的重要因素,算法收敛速度越快,需要的训练序列越短,需要消耗的时频资源就越少. 图 5所示为2种算法的收敛曲线.

|
图 5 不同算法的收敛曲线 |
由图 5可以看出,基于降维的局部NLMS波束赋形算法和二维阵列全局NLMS波束赋形算法收敛速度相当.由于二维阵列全局NLMS波束赋形算法能对每个阵元的权值进行相对独立的调整,而基于降维的局部NLMS波束赋形算法仅对阵列中的一行和一列进行调整,其余阵元的权值是根据这些阵元的权值进行计算的,因此其阵元权值对应的累积误差较大、误差波动也相对较大,但这对波束赋形的效果影响并不明显.
4 结束语以NLMS算法为例,通过理论分析和仿真验证了二维阵列的全局自适应算法和基于降维的局部自适应算法调整阵列天线各阵元的权值可以实现对期望方向的三维波束赋形.二维阵列的全局NLMS算法形成的波束旁瓣较小,但其运算量较大. 2种算法的收敛速度相当,而二维阵列的全局NLMS算法收敛精度较高.下一步将研究三维阵列天线的自适应波束赋形算法来实现更加精确的三维波束赋形,同时研究快速的自适应波束赋形算法减少运算复杂度,提高算法收敛速度及精度.
| [1] | Koppenborg J, Halbauer H, Saur S, et al. 3D beamforming trials with an active antenna array[C]//Smart Antennas (WSA), 2012 International ITG Workshop on. Piscataway, N. J.: IEEE, 2012: 110-114. |
| [2] | Sun Yongjiang, Qiu Dongdong, Rao Jiaren, et al. Research on adaptive beamforming algorithm[C]//Image Analysis and Signal Processing (IASP), 2012 International Conference on. Piscataway, N. J.: IEEE, 2012: 1-3. |
| [3] | Saur S, Halbauer H. Exploring the vertical dimension of dynamic beam steering[C]//Multi-Carrier Systems & Solutions (MC-SS), 2011 8th International Workshop on. Piscataway, N. J.: IEEE, 2011: 1-5. https://www.researchgate.net/profile/Hardy_Halbauer/publication/252011232_Exploring_the_vertical_dimension_of_dynamic_beam_steering/links/5460a7a60cf27487b4516727.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail |
| [4] | Halbauer H, Saur S, Koppenborg J, et al. Interference avoidance with dynamic vertical beamsteering in real deployments[C]//Wireless Communications and Networking Conference Workshops (WCNCW), 2012 IEEE. Piscataway, N. J.: IEEE, 2012: 294-299. |
| [5] | Yasin M, Akhtar P, Valiuddin D. Performance analysis of LMS and NLMS algorithms for a smart antenna system[J].International Journal of Computer Applications, 2010, 4(9): 25–32. doi: 10.5120/ijca |
| [6] | Yang Qun, Cao Xiangyu, Yao Xu, et al. Performance of LMS algorithm in smart antenna[C]//Microwave and Millimeter Wave Technology (ICMMT), 2010 International Conference on. Piscataway, N. J.: IEEE, 2010: 1372-1375. |


