针对传统算法将残留载波间干扰(ICI)当白噪声处理引起系统性能下降的问题,提出一种白化残留ICI和噪声的最优线性ICI消除算法.首先对残留ICI和噪声进行白化,其次基于最大化系统可达速率,推出了最优线性ICI消除矩阵,并结合连续干扰消除算法,实现了时变信道带来的时间分集.仿真结果表明,该算法克服了传统算法带状近似引起系统性能损失的缺点,并适用于当前信道估计精度下的OFDM系统.
To reduce the complexity, the existing algorithms treat the residual inter-carrier interference (ICI) as white noise, which causes a decline in system performance. Consequently, an optimal linear ICI cancellation algorithm based on whitening residual ICI and noise was proposed. Firstly, the whiten matrix is constructed to whiten the residual ICI and noise simultaneously. Then, the optimal linear ICI cancellation matrix was deduced by maximizing the achievable rate in orthogonal frequency division multiplexing (OFDM) systems, which can obtain the time diversity embedded in time variant channels combining with successive interference cancellation. Simulations show that the proposed algorithm obviates the performance loss introduced by band approximation in traditional algorithms and can apply to OFDM systems in the channel estimation accuracy at present.
正交频分复用(OFDM,orthogonal frequency division multiplexing)作为一种高速无线传输技术具有抗多径能力强、频谱利用率高、在实际系统中易于实现等优点,已广泛应用到DVB、DAB、IEEE 802.11.a、IEEE 802.16g以及3GPP LTE等众多通信标准中[1].传统OFDM系统的研究均基于信道在一个OFDM符号内准静态的假设.然而,当前可演进到4G的通信标准,如WiMAX提出的802.16m和3GPP提出的LTE,都需提供终端移动速度超过120 km/h移动场景下的宽带通信服务[2].终端高速移动产生的多普勒频移导致信道随时间变化,破坏了子载波间的正交性,产生载波间干扰(ICI, inter-carrier interference).在接收端,不同入射角的传播路径具有不同的多普勒频移,多条路径信号叠加后形成多普勒扩展,估计出的频偏无法对准每一路径的频率偏移,通过单一频偏估计消除ICI的方法不再适用.因此,研究时变信道下如何消除OFDM在高信噪比时出现的误码地板具有重要意义.
时不变信道下的OFDM系统将频率选择性信道转换成平坦衰落信道,只需一个简单的单抽头均衡器就能估计信道并恢复数据.然而,在通信终端高速移动产生ICI的情况下,各子载波间相互耦合使得接收端的检测和均衡变得复杂.近些年来,国内外学者对ICI特性及其抑制方法进行了大量研究. Cai等[3]推导出双选瑞丽衰落信道下OFDM传输匹配滤波的性能界,并指出时变信道引起的大部分符号能量泄漏分布在少量子载波上,当前子载波上的ICI功率主要来自相邻几个子载波.基于该结论,文献[4-6]为降低算法实现复杂度对频域信道矩阵进行带状近似,该算法在较小的归一化多普勒频移下接近性能界,但当归一化多普勒频移较大时,信道矩阵的带状简化不符合实际信道的时变特性,没有充分利用所有观测元素,从而导致系统性能损失.
针对该问题提出一种基于白化残留ICI和噪声的最优线性ICI消除算法.并结合连续干扰消除,实现时变信道带来的时间分集,最后利用LDLH分解实现检测过程中的矩阵求逆,使算法在实际系统中易于实现.
文中涉及的各符号含义如下:(·)T和(·)H分别表示转置和共轭转置,(·)-1表示矩阵求逆,(x)N表示对x进行模N操作.大写字母加粗表示矩阵,小写字母加粗表示矢量. |·|表示取模值. FN和FNH分别表示N点的傅里叶变换和逆傅里叶变换矩阵. X(i:j, m:n)表示取矩阵X的第i到j行和第m到n列的元素组成的矩阵.
1 载波间干扰分析考虑具有N个子载波的OFDM系统,假设系统完全同步且循环前缀(CP,cyclic prefix)长度大于信道的最大时延扩展L-1.对于任意一个OFDM符号,输入-输出关系可表示为

|
(1) |
其中:


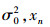
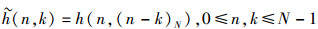

|
(2) |
其中:gk, m表示第m个子载波对第k个子载波的干扰系数,其中
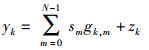
|
(3) |
将式(2) 代入式(3) 可得

|
(4) |
其中: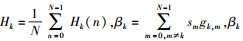
由干扰系数的表达式(2) 可看出各子载波间相互耦合,相比于传统基于信道在一个OFDM符号内时不变的假设,时变信道下接收端的检测和均衡变得复杂.传统算法为了简化接收机设计并降低检测复杂度,只考虑邻近2Q个子载波带来的干扰,根据该思想将式(3) 写成带内干扰和带外干扰2部分
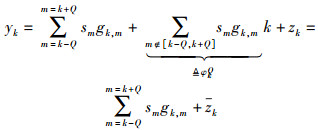
|
(5) |
其中: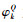
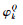
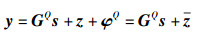
|
(6) |
其中:
然而,由于残留ICI具有很强的相关性,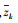
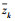
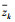
以下讨论均假设可通过信道估计来获得精确的信道频率响应矩阵G.定义z的协方差矩阵为D,由于φQ和z不相关,则D可表示为
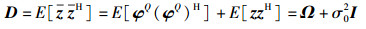
|
(7) |
其中:Ω表示残留ICI的自相关矩阵,I表示单位矩阵,利用文献[7]的结论,其元素可表示为
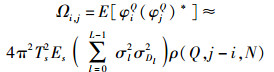
|
其中:Ts为采样间隔,Es为符号能量,σl2和σDl2分别表示第l条径的延时功率分布和均方多普勒扩展,ρ(Q, j-i, N)表示特定的级数求和,其具体计算过程可参考文献[7].
对式(6) 中的z进行白化,可得

|
(8) |
其中:
下面通过最大化系统可达速率推导出最优线性ICI消除算法.线性ICI消除方法可统一表示为

|
(9) |
其中: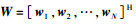

|
(10) |
其中:σj2为第j个子载波上的发送功率,在发送端未知信道信息的情况下,假设对每个子载波分配相同的功率σs2. ei表示第i个元素为1其他元素为0的N×1维单位矢量.式(10) 可表示为
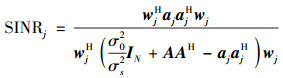
|
(11) |
可得如下最优化问题
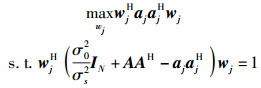
|
求解该最优化问题可得第j个子载波最优线性ICI消除矢量.因此,最优线性ICI消除矩阵W为

|
(12) |
连续干扰消除检测性能通常优于单次检测,可将以上方法扩展到非线性ICI抑制.首先检测出正确检测概率最大的信号,基于准则:fk= 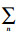

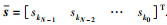
式(8) 变为
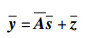
|
(13) |
根据检测顺序sk0, sk1, …, skN-1,首次检测sk0时,求出检测矢量w0,得到判决量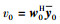
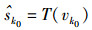

1) 将信道矩阵G带状近似为GQ,并将残留ICI和白噪声合并为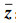
2) 构造白化矩阵D-1/2对残留ICI和白噪声进行白化得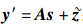
3) 排序后可得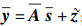
4) 计算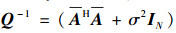
5) 计算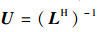
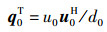
6) 计算
7) 对于j=1, 2, …, N-1;
计算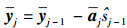
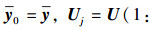
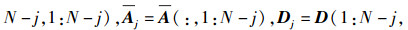
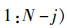
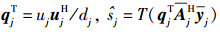
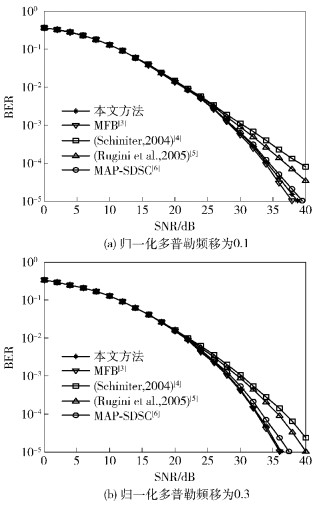
在时变信道环境下的OFDM系统中,对提出的算法进行仿真.仿真参数选取如下:子载波个数N=128,循环前缀长度Ncp=16,载波频率为2.4GHz,系统带宽为1 MHz,采用16-QAM调制,时变信道采用文献[7]中的Jakes模型,最大归一化多普勒频移fdTs分别取0.1和0.3.将提出算法与文献[4-6]中所提的带状近似算法进行比较.同时给出匹配滤波器限(MFB,matched filter bound)[3]曲线.
在信道信息精确已知的假设下,仿真结果如图 1所示.由图 1可看出,本算法的性能在不同的归一化多普勒频移下均优于对信道矩阵进行带状近似的传统算法,并且接近MFB曲线;随着最大归一化多普勒频移的增加,系统性能提升,这是因为本算法利用了传统算法摒弃的部分信道信息,可有效地实现该时间分集.
|
图 1 不同算法的BER性能曲线比较 |
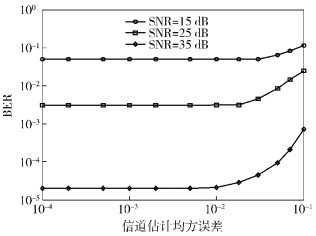
以上均以信道矩阵精确已知为前提,下面通过仿真研究信道估计误差对该算法性能的影响. 图 2给出了归一化多普勒频移为0.3时,不同SNR下信道估计误差对本算法性能的影响.由图 2可看出,当信道估计均方误差小于0.01,算法的性能基本不受影响,且系统性能随着SNR的增大对信道的估计误差更敏感,这是由于信道估计误差会引入额外的ICI,当SNR较大时,系统性能主要受ICI的影响,对信道估计误差带来的ICI比较敏感,当SNR较低时,系统性能主要受噪声的影响,因此对信道估计误差不敏感.当前快时变OFDM系统的信道估计误差[8]可达到0.01以下,适用于当前的OFDM系统.
|
图 2 信道估计误差对算法性能影响 |
与对比算法的文献相同,采用复数乘法和复数加法的总操作次数来衡量算法的计算复杂度.不同算法的计算复杂度比较如表 1所示.
|
|
表 1 不同算法的计算复杂度比较 |
结合性能比较和表 1的复杂度对比可看出,虽然本算法计算复杂度较高,但在归一化多普勒频移较大的场景下系统性能接近MFB的理论极限性能.在存在大动态多普勒且对系统性能要求较高的场景下具有重要的应用意义,如何降低该方法的计算复杂度是进一步需要研究的问题.
4 结束语针对传统ICI消除算法对时变信道矩阵进行带状近似所导致的系统性能下降问题,首先对残留ICI和噪声进行白化,其次从最大化系统可达速率的角度,推导出了最优线性ICI线性消除矩阵,并结合连续干扰消除算法进一步扩展为非线性ICI消除,最后基于复杂度及可实现性的考虑,利用LDLH分解来实现检测过程中的矩阵求逆运算.分析与仿真表明,本算法克服了传统算法将残留ICI当白噪声处理引起性能损失的缺点;当信道估计均方误差小于0.01时,本算法具有很好的鲁棒性.
| [1] | Chen Shaoping, Dai Guangfa, Rao Wengui. ICI mitigation and diversity gain for OFDM systems in time-varying multipath fading channels[J].European Transactions on Telecommunications, 2011, 22(2): 61–67. doi: 10.1002/ett.1458 |
| [2] | Senol H, Poor H V. Joint channel estimation, equalization, and data detection for OFDM systems in the presence of very high mobility[J].IEEE Transactions on Signal Processing, 2010, 58(8): 4225–4238. doi: 10.1109/TSP.2010.2048317 |
| [3] | Cai Xiaodong, Georgios B G. Bounding performance and duppressing intercarrier interference in wireless mobile OFDM[J].IEEE Trans on Commun, 2003, 51(12): 2047–2056. doi: 10.1109/TCOMM.2003.820752 |
| [4] | Schniter P. Low-complexity equalization of OFDM in doubly-selective channels[J].IEEE Trans on Signal Processing, 2004, 52(4): 1002–1011. doi: 10.1109/TSP.2004.823503 |
| [5] | Luca R, Paolo B, Geert L. Simple equalization of time-varying channels for OFDM[J].IEEE Communications Letters, 2005, 9(7): 619–621. doi: 10.1109/LCOMM.2005.1461683 |
| [6] | Panayirci E, Dogan H, Vincent P H. Low-complexity MAP-based successive data detection for coded OFDM systems over highly mobile wireless channels[J].IEEE Trans on Veh Technol, 2011, 60(6): 2849–2857. doi: 10.1109/TVT.2011.2158564 |
| [7] | Wang Haiwei, Lin David W, Tzu-Hsien Sang. OFDM signal detection in doubly selectie channels with blockwise whitening of residual intercarrier interference and noise[J].IEEE Journal On Selected Areas in Communications, 2012, 30(4): 684–694. doi: 10.1109/JSAC.2012.120503 |
| [8] | Tomasz H, Saptarshi D, Gerald M, et al. Practical estimation of rapidly varying channels for OFDM systems[J].IEEE Trans on Commun, 2011, 59(11): 3040–3048. doi: 10.1109/TCOMM.2011.082111.110075 |



