2. 北京交通大学 电子信息工程学院,北京 100044
针对传统正交频分复用降低峰均功率比算法计算复杂度较高,失真比较严重的问题,提出了一种改进的限幅滤波算法,该算法将正交频分复用信号划分为奇信号与偶信号来分别进行限幅滤波操作.仿真结果表明,与传统的限幅滤波算法相比,该算法在降低峰均功率比(PAPR)的同时,具有较低的计算复杂度,同时能较好地滤除带外干扰,显著提高系统的误码率的性能.
2. School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China
An improved clipping and filtering algorithm was proposed to improve the currently used algorithms for reducing peak-to-average power ratio (PAPR) of orthogonal frequency division multiplexing (OFDM) with high computational complexity and serious distortion. The algorithm divides OFDM signals into odd signals and even signals. And the two kinds of signals are clipped and filtered. Simulation shows that, in comparison with currently used clipping and filtering algorithms, the algorithm is with better PAPR performance with lower computational complexity and filters in-band interference more obviously. The bit error rate performance of the system can be improved through the algorithm.
正交频分复用(OFDM,orthogonal frequency division multiplexing)是一种多载波(MCM,multi-carriers modulation)传输技术,具有很多其他无线通信技术所无法比拟的优势,成为下一代无线通信系统的关键技术之一[1]. OFDM技术的一个主要的缺点是其具有较高的峰均功率比(PAPR,peak-to-average-power ratio)[2].限幅是一种最为简单的降低PAPR的方法,其核心思想是给定一个阈值,将OFDM信号中超过阈值的部分直接进行削波处理,使其不会超过放大器的动态变化范围[3].但由于该技术是一个非线性的过程,将会带来严重的带内失真和带外干扰,会影响整个系统的误比特率性能与频谱效率[4]. Jean A[5]提出了一种迭代限幅滤波算法,能够有效地解决带外干扰的问题.但每进行一次迭代需要进行3次FFT/IFFT变换,从而引入了较高的计算复杂度.同时,由于限幅操作会带来严重的带内失真和带外干扰,会影响整个系统的误码率性能与频谱效率[6].
为此,提出了一种改进的迭代限幅滤波算法,该算法将OFDM信号划分为奇信号与偶信号来分别进行限幅滤波操作.该算法在降低PAPR性能的同时,具有较低的计算复杂度,同时能滤除带外干扰,显著提高系统的BER性能.
1 改进的限幅滤波算法1.1 算法原理令OFDM的频域信号

|
(1) |
其中:
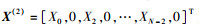
对X进行IFFT变换,即有

|
(2) |
其中:x(1)为X(1)经IFFT变换之后的时域信号,x(2)为X(2)经IFFT变换之后的时域信号.
令
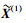

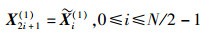
|
(3) |
如果
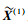

|
(4) |
令
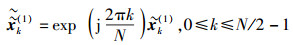
|
(5) |



|
(6) |
则

|
(7) |
同理,令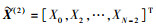


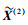
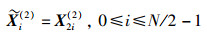
|
(8) |
如果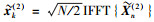

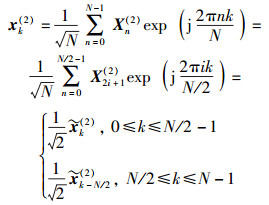
|
(9) |
则
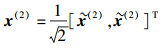
|
(10) |
由式(7) 与式(10) 可知,奇信号与偶信号的OFDM调制都能由N阶IFFT变换降为N/2阶的IFFT变换来实现.对奇信号,首先需要对其的IFFT变换结果



|
(11) |
由式(11) 可知,x的PAPR性能是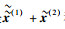

在1.1节分析的基础上,提出了一种改进的限幅滤波算法,如图 1所示为改进的限幅滤波算法的系统框图.

|
图 1 改进的限幅滤波算法系统框图 |
改进的限幅滤波算法的具体操作步骤如下.
1) 将频域信号


2) 对奇信号与偶信号分别进行L倍过采样,得到信号
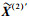
3) 将奇信号的时域信号进行相移,并将其与偶信号的时域信号分别送入限幅滤波模块,具体操作将在后文中进行详细介绍.
4) 对进行了限幅滤波操作之后的奇信号

由式(11) 可知,当

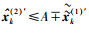
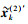

|
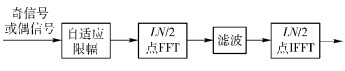
图 2 限幅滤波模块框图 |
以偶信号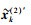

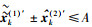
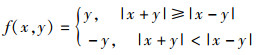
|
(12) |
在对偶信号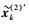


|
(13) |
如图 3所示.
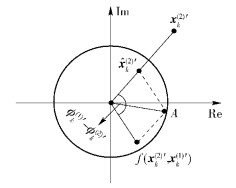
|
图 3 自适应限幅操作的示意图 |
其中,
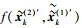
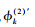


|
(14) |
那么可得偶信号的自适应限幅的表达式为
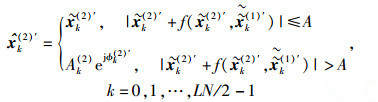
|
(15) |
然后对限幅操作后的偶信号
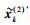
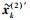

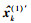

|
(16) |
则奇信号的自适应限幅阈值为
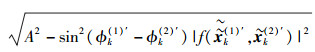
|
(17) |
奇信号的自适应限幅表达式为

|
(18) |
然后对限幅操作后的奇信号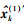
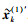
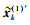
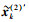
由于限幅操作会带来严重的带内失真和带外干扰,影响整个系统的误码率性能与频谱效率.为此需要对信号进行滤波和噪声消除,以避免带外干扰和带内失真造成的系统性能下降.目前有一种由Chen Hangjun和Alexander H提出的频域噪声消除算法(NC, noise cancellation)[6],能从频域出发而在接收端估计限幅噪声,由此消除其干扰.其实现框图如图 4所示.其基本思想是估算出限幅噪声,并从原始信号中去除限幅噪声的影响. 图 4中虚线模块部分为传统的限幅滤波算法,用如图 1所示的改进的迭代限幅滤波算法将其替换,可得到一种改进的频域噪声消除算法,能滤除带外干扰,提高系统的BER性能.

|
图 4 频域噪声消除算法的实现框图 |
传统的迭代限幅滤波算法中,每进行一次迭代处理需要一次LN阶的FFT和IFFT变换,复数乘法的运算量为LN/2lbLN,复数加法的运算量为LNlbLN.而笔者所提出的改进的限幅滤波算法,每次迭代中包括2次LN/2阶的FFT与IFFT变换,再加上该算法中还包括相移、信号扩展和转置操作,则其计算复杂度应比传统的算法略低.而由于改进的限幅滤波算法在每次迭代中进行了2次限幅滤波的操作,则整个系统降低PAPR的性能收敛速度较传统算法更快.
2 仿真结果采用子载波数为N=1 024的输入信号,过采样因子为L=4;限幅比(CR, clipping ratio)为1.993和2.512,所对应的限幅阈值分别为6 dB和8 dB;限幅滤波的迭代次数为4.
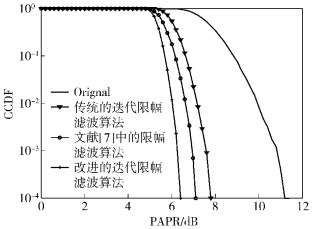
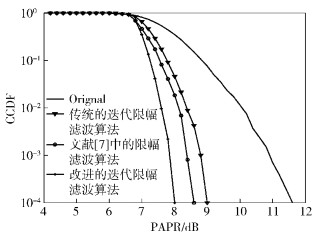
图 5与图 6分别表征了在不同的限幅阈值的情况下,传统的迭代限幅滤波算法与提出的改进的迭代限幅滤波算法降低PAPR的性能比较.通过图 5和图 6可见,笔者提出的改进的算法降低PAPR的性能要优于传统的迭代限幅滤波算法和文献[7]提出的限幅滤波算法.当限幅阈值为6 dB,互补累计分布函数(CCDF, Complementary Cumulative Distribution Function)为10-4时,改进的迭代限幅滤波算法能够比传统的迭代限幅滤波算法多获得1.3 dB左右的PAPR性能增益,比文献[7]提出的限幅滤波算法多获得0.8 dB左右的PAPR性能增益;而当限幅阈值为8 dB,CCDF=10-4时,改进的迭代限幅滤波算法能够比传统的迭代限幅滤波算法多获得1 dB左右的PAPR性能增益,比文献[7]提出的限幅滤波算法多获得0.6 dB左右的PAPR性能增益.
|
图 5 限幅阈值为6 dB时,PAPR性能对比曲线 |
|
图 6 限幅阈值为8 dB时,PAPR性能对比曲线 |
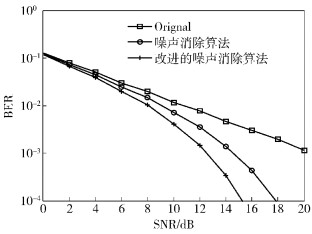
图 7显示了当采用子载波数为N=1 024的输入信号,过采样因子为L=4,限幅因子为CR=1.993,即限幅阈值为6 dB,信道为加性高斯白噪声信道时,在接收端使用频域噪声消除算法以及改进的频域噪声消除算法之后,系统的误码率BER(BER, bit error ratio)性能.由图 7可见,改进的噪声消除算法能显著提高系统的BER性能,当BER为10-4时,相比噪声消除算法,改进的噪声消除算法能获得超过2 dB的BER性能增益.
|
图 7 BER性能对比曲线 |
将传统的限幅滤波算法加以改进,在进行限幅操作之前首先将信号划分为奇信号与偶信号,之后分别对其进行限幅操作,从而达到降低整体系统的PAPR的目的.同时,针对限幅操作会带来严重的带内失真和带外干扰的问题,在接收端采用了噪声消除算法,并与改进的迭代限幅滤波算法相结合,得到一种改进的噪声消除算法,能够从频域出发而在接收端估计限幅噪声,由此消除其干扰.仿真结果表明,与传统的迭代限幅滤波算法相比,该算法在降低PAPR性能的同时能较好地滤除带外干扰,显著提高系统的BER性能.
| [1] | Chen Shanzhi, Wang Yingmin, Ma Weiguo, et al. Technical innovations promoting standard evolution: from TD-SCDMA to TD-LTE and beyond[J].IEEE Wireless Communications, 2012, 19(1): 60–66. doi: 10.1109/MWC.2012.6155877 |
| [2] | Zhu Xiaodong, Pan Wensheng, Li Hong, et al. Simplified approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].IEEE Transactions on Communications, 2013, 61(5): 1891–1901. doi: 10.1109/TCOMM.2013.021913.110867 |
| [3] | Wang Yongchao, Luo Zhiquan. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].IEEE Transactions on Communications, 2011, 59(1): 33–37. doi: 10.1109/TCOMM.2010.102910.090040 |
| [4] | Ahmad R S B, Manoneet S. A new approach for evaluating clipping distortion in multicarrier systems[J].IEEE Journal on Selected Areas in Communications, 2002, 20(5): 1037–1046. doi: 10.1109/JSAC.2002.1007384 |
| [5] | Jean A. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering[J].Electronics Letters, 2002, 38(5): 246–247. doi: 10.1049/el:20020175 |
| [6] | Chen Hangjun, Alexander H. Iterative estimation and cancellation of clipping noise for OFDM signals[J].IEEE Communications Letters, 2003, 7(7): 305–307. doi: 10.1109/LCOMM.2003.814720 |
| [7] | Yu Hua, Wei Gang. Choosing the optimal clipping ratio for clipping and filtering PAR-reduction scheme in OFDM[C]//International Conference on Wireless Communications, Networking and Mobile Computing. Shanghai: IEEE, 2007: 460-463. |


