2. 浙江省服装工程技术研究中心, 杭州 310018;
3. 北京邮电大学 电子工程学院, 北京 100876
针对服装企业产品销售的复杂性以及特殊性,提出一种有效的神经网络学习模型.在对服装销售影响因子分析的基础上建立销售预测网络模型,利用遗传算法对后向传播神经网络的各连接权值进行优化计算.方法综合了后向传播神经网格和遗传算法两者的优势,既具有神经网络强大的学习能力,又具有遗传算法的全局搜索能力.
2. Engineering Research Center of Clothing of Zhejiang Province, Hangzhou 310018, China;
3. School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
The neural network learning models was proposed, focusing on complexity and particularity of product sales in garment industry. The network model was established to predict the impact on garment sales on basis of factor analysis and optimized by using genetic algorithms for each connection weights of back propagation (BP) neural network. The method combines the strong learning ability of the BP neural and the global search capability of genetic algorithms.
基于人工神经网络构建销售预测模型,是预测未来销售情况最为有效的方法之一[1]. 2009年,Coskun H等[2]在周期性时间序列预测研究中,使用迭代人工神经网络进行建模,并对直接预测和迭代预测2种方法进行了比较.中国台湾学者Wang Taiyue等[3]使用模糊神经网络对台湾制造业的创新绩效进行了预测研究,实现了一种适应性类模糊神经网络推论系统. 2010年,Mehdi K等[4]提出了一种新的基于时间序列和人工神经网络的自动平滑整合模型. 2011年,Tsan M C[5]提出了一种最大程度学习机制对人工神经网络进行了优化,并通过对某品牌销量数据的学习训练,准确预测了服装产品的月销量.张闯等[6]采用后向传播(BP,back propagation)神经网络预测方法, 通过新浪微博数据预测电影票房.神经网络结构的优劣影响着整个网络的学习训练速率和收敛速度,过少的网络节点可能导致输出结果产生大的误差,而过多的网络节点却可能导致整个网络的学习时间延长,收敛速度变慢.笔者在对服装销售影响因素分析的基础上,构建BP网络模型,并通过遗传算法对BP网络的各连接层参数进行优化,经过多次反复训练确定最优权值的阀值范围.
1 遗传算法优化BP神经网络目前,BP神经网络凭借其强大的自适应学习能力已被广泛应用,取得了较好的成效,但在实际应用中其学习训练的结果有时也会出现较大误差.究其原因,主要是因为BP神经网络自身仍存在很多缺点.例如,BP神经网络的学习速率慢,网络训练失败的可能性较大.其隐层层数与节点数的选取在目前情况下尚无指导理论可供参考,多数情况下,研究者是根据经验和反复试验来确定隐层层数与节数.
通过遗传算法优化BP神经网络的各连接层参数,经过反复不断的训练调整,最终确定网络的最优权值阀值.通过实践证明,借助遗传算法对BP神经网络的初始权值阀值进行优化,可以取得较好的效果.采用遗传算法优化BP神经网络各连接层权值阀值的过程如下:
1) 通过遗传编码操作,对随机赋予的初始权值阀值进行遗传编码,得到随机分布的序列串,每一个序列串对应一组网络中各连结层的权值阀值;
2) 输入训练样本,计算目标输出与实际输出的误差绝对值,计算适应度函数值,以此评价网络连接权值阀值的优劣性;
3) 比较适应度函数值,选择适应度函数值较大的个体,直接遗传给子代;
4) 进行交叉和变异操作,产生新的子代种群;
5) 重复2)~4) 步,不断进化初始权值阀值,直到训练目标满足条件为止,得到最优权值阀值.
采用遗传算法优化BP神经网络结构的过程如下:
1) 随机产生多个网络结构,使用“0-1”字符串对所有网络结构进行表示,每组字符串对应一种网络结构,其中“0”代表连接层节点之间无连接,“1”代表连接层节点之间有连接;
2) 对所有网络节点随机赋予不同的权值阀值,反复学习训练;
3) 计算每个网络结构经学习训练后得到的实际输出与目标输出之间的误差,由此计算适应度函数值,适值以绝对误差和表示;
4) 比较3) 步得到适应度函数值,选择适应度函数值最小的个体遗传给下一代种群;
5) 进行交叉操作和变异操作,产生新子代种群;
6) 重复2)~5) 步,直到达到终止条件,得到最优个体.
考虑借助遗传算法设计并优化BP神经网络的学习规则,克服BP网络自身收敛速度慢、易陷入局部最小值的缺点.
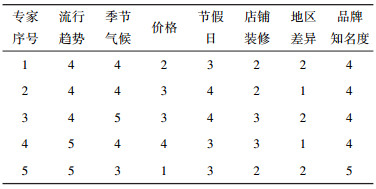
2 服装销售预测模型的建立2.1 模型的网络结构设计服装产品其销售情况受到各种复杂因素的影响,如时尚流行趋势、季节气候变化、产品价格、节假日、店铺装修、地区消费差异、品牌知名度等.将上述影响因子作为输入量构建预测.针对这些影响因子,选择5位在服装行业具有多年销售经验的职业经理人进行打分.最高分设为5分,随着分值减小,其对销售的影响程度逐渐减小.打分统计如表 1所示.
|
|
表 1 影响服装销售的宏观因子专家打分统计表 |
采用式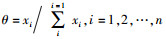
|
|
表 2 影响服装销售的宏观因子权值表 |
从平均权重w可发现,流行趋势、季节气候变化、品牌知名度以及节假日等4个因素的权重相对较大,说明其对服装产品销量产生的影响也相应较大.实际上,流行趋势具有持续的动态变化特征,而流行元素也涉及面料、款式、色彩等多个方面,因此基于历史销售数据很难挖掘出典型特征性数据.选取2012年某月份某品类的月销售量Sy、节假日因子(同月所有产品平均销量Sa)、季节因子H、品类因子C作为输入量,产品当年当月的销售量S作为输出量,构建相应的网络模型.
2.2 预测模型的算法设计预测算法包括3个步骤:BP神经网络确定、遗传算法优化计算和BP神经网络预测.
1) 整理历史销售数据,根据服装销售的影响因子,确定样本数据集,同时建立网络拓扑结构,并初始化各连接点权值;
2) 采用遗传算法优化计算各连接层的权值;
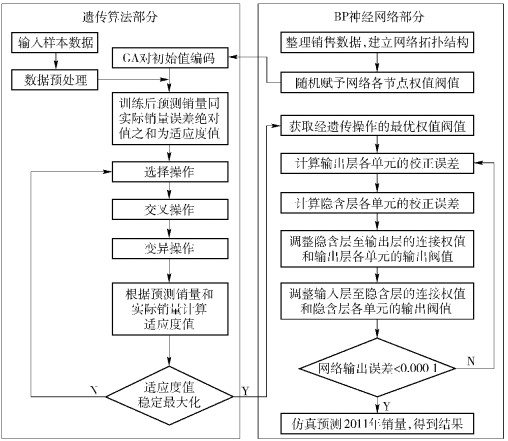
3) 利用BP神经网络进行预测,算法流程如图 1所示.
|
图 1 算法程序流程 |
选用了最为常见的3层BP神经网络模型,如图 2所示.

|
图 2 3层BP神经网络拓扑结构 |
在网络中设置较少的隐层节点数,然后逐渐增加隐含层节点数,并使用同一训练样本集重复进行多次训练,当误差达到最小时,其隐层节点数即为网络的最佳隐层节点数.
2.4 预测模型的建模步骤1) 销售数据的预处理
采用以下归一化方法将数据变换到[0, 1]区间.
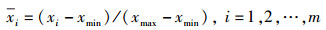
|
其中:xi代表输入或输出数据,xmin代表数据变化范围的最小值,xmax代表数据变化范围的最大值.
2) 优化初始权值
采用遗传算法的优化学习过程如下:
① 初始化种群P,包括交叉规模,交叉概率Pc(Pc=0.5,0.6,0.8),变异概率Pm(Pm=0.001,0.005,0.01),在编码过程中,采用实数进行编码,初始种群n=20,通过初始化试算,可发现随着交叉概率的增大,种群的随机化开始加大,随着变异概率的增大,种群的多样性开始扩大,随着种群规模的不断增大,算法陷入局部最优解的危险减小;
② 计算个体适应度函数值,将预测输出值和目标输出值之间的绝对误差之和作为个体适应度函数值F;
③ 采用适应度比例选择法进行遗传算子运算,根据个体适应度占群体的比例分配来选择子代个体;
④ 采用实数交叉算子,进行交叉操作,以交叉概率Pc对个体Gi和Gi+1进行交叉操作,产生新的子代个体,对没有进行交叉操作的个体直接进行复制操作;
⑤ 采用非均匀变异算子,进行变异操作,利用变异概率Pm突变产生Gj的新个体G′j;
⑥ 将新个体插入到种群P中,计算新个体的适值;
⑦ 如果找到了满意的子代个体,则算法结束,否则转入步骤③ 继续操作.
3) 建立BP神经网络模型
对于确立的BP神经网络参数建立网络模型,将经过遗传算法优化后得到的最优个体重新赋值给BP神经网络各连接层的初始权值阀值.然后,将归一化处理后的样本数据送入BP神经网络进行学习操作,反复训练,最终根据网络性能的优劣程度确定网络的系统参数,最终确立BP网络模型.
4) 销售预测
将归一化后的预测样本数据送入到训练好的BP网络模型中,预测输出数据,并进行反归一化处理.
5) 网络模型的评价
经过网络模型学习、训练、预测后,采用平均绝对误差(MAE, mean absolute error)、平方和误差(SSE, sum of squares error)、均方误差(MSE, error of mean square)将预测输出结果同目标输出的实际值进行对比分析,对系统模型性能进行总结评价.
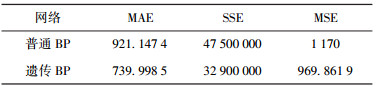
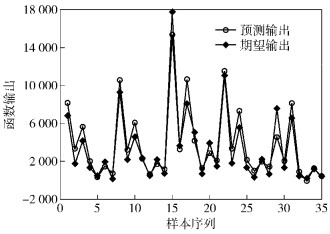
3 实验论证以X品牌的销量预测进行验证.选取2008-2010年连续3年在杭州5-9月的历史销量数据为训练样本.对女装7个品类以及男装4个品类进行月销量预测.以2011年杭州地区同时段的销量数据为预测样本检验预测性能.女装产品分为短T恤、短衬衫、长裤、短裤、半身裙、连身裙以及背心7个类别;男装产品分为短T恤、短衬衫、长裤以及短裤4个类别. 表 3所示为每类产品的当月销售量.设学习率为0.1, 期望误差为0.000 1.在输入同样的学习样本和预测样本后,预测结果如图 3和图 4所示,“
|
|
表 3 X品牌女装销量预测 |
|
图 3 使用普通BP网络的X品牌女装预测结果 |
|
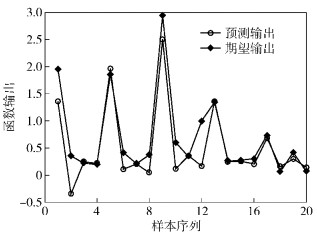
图 4 使用普通BP网络的X品牌男装预测结果 |
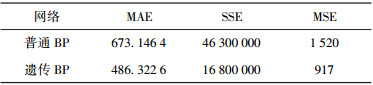
使用未经优化的普通BP神经网络和经过遗传算法优化BP神经网络模型的平均绝对误差、平方差、均方差如表 3和表 4所示,经过遗传算法优化后的BP网络其误差值小于普通BP神经网络的误差值,说明遗传BP网络模型优于普通BP网络模型.
|
|
表 4 X品牌男装销量预测 |
实验证明,相比于未经优化的普通BP神经网络,使用遗传算法优化后的BP神经网络其预测结果精度更高,同时避免了普通BP神经网络学习训练收敛速度慢、容易陷入局部最小值等缺点,并且在实际销售预测中更能准确反映产品销售趋势.借助遗传算法的特点,将其应用于BP神经网络建模预测过程中,可有效地避免BP网络的缺点,集合2种算法的优势,提高了预测精度和收敛速度.
| [1] | Celia F, Amar R, Les S. Forecasting women's apparel sales using mathematical modeling[J].Forecasting Women's Apparel Sales, 2005, 24(3): 108–121. |
| [2] | Coskun H, Diyar A. Comparison of direct and iterative artificial neural network forecast approaches in multi-periodic time series forecasting[J].Expert Systems with Applications: An International Journal, 2009, 36(2): 76–81. |
| [3] | Wang Taiyue, Lin Suli. Application of neuro fuzzy networks to forecast innovation performance—the example of taiwanese manufacturing industry[J].Expert Systems with Applications: An International Journal, 2010, 37(2): 56–59. |
| [4] | Mehdi K, Mehdi B. An artificial neural network model for time series forecasting[J].Expert Systems with Applications: An International Journal, 2010, 37(1): 64–68. |
| [5] | Tsan M C. An intelligent fast sales forecasting model for fashion products[J].Expert Systems with Applications: An International Journal, 2011, 38(6): 77–80. |
| [6] |
张闯, 姜杨, 吴铭, 等. 基于社会化媒体节点属性的信息预测[J]. 北京邮电大学学报, 2012, 35(4): 24–27.
Zhang Chuang, Jiang Yang, Wu Ming, et al. Information predictions based on node attributes of social media[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 24–27. |