为了提高二线性迭代最小二乘(BALS)算法拟合平行因子(PARAFAC)模型的速度,提出了一种新的PARAFAC模型拟合算法.该算法利用新迭代与旧迭代之间的增量值,来预测下一次迭代的初始值,对BALS中的每次迭代,为2个加载矩阵设置相应的松弛因子,并通过联合优化的方法求得最优松弛因子对,从而加速BALS的收敛速度.理论分析和仿真结果表明,与已有的BALS算法相比,所提算法在不牺牲性能的条件下,有效地提高了PARAFAC模型的拟合速度.
To speed up the convergence of the bilinear alternating least squares (BALS) algorithm of fitting the parallel factor (PARAFAC) model, a new algorithm of fitting the PARAFAC model was proposed. In each iteration, the proposed algorithm sets up their own relaxation factors for two loading matrices which are required to be estimated, and gets the optimal couple of two relaxation factors by the joint optimization. Analysis and simulation show that the proposed algorithm improves the speed of fitting the PARAFAC model without performance deterioration compared with the existing BALS algorithm.
PARAFAC模型[1]的3个维度可与无线通信中的空域、时域和频域(或码域)结合起来,无需信道、扩频码和信号等具体信息,就能实现信号检测和信道估计.因此,PARAFAC模型已得到相关学者的广泛关注和研究[2-3].在拟合PARAFAC模型的众多算法中,三线性交替最小二乘(TALS, trilinear alternating least square)算法由于简单易行,且易与其他算法结合,因此使用最为广泛.但是,由于TALS存在许多无效迭代,特别是加载矩阵中存在几乎共线性的列向量时,TALS算法需要大量的迭代次数来达到收敛.为了提高TALS算法的收敛速度,线性搜索算法[4]和加强线性搜索算法[5-7]相继被提出.对TALS中的所有迭代分别取固定的松弛因子n(n为迭代次数)的三次方根[4],对TALS中每次迭代都求最优的单实数松弛因子[5],而文献[6]和文献[7]中对TALS中每次迭代都求最优的单复数松弛因子.上述几种算法虽然在一定程度上提高了TALS的收敛速度,但仍需要较多的迭代次数,且TALS算法的拟合精度并未得到提高.若已知TALS中的一个加载矩阵,TALS算法演化为BALS算法[1, 8].同等条件下,BALS算法所需迭代次数和单次迭代的计算复杂度都小于TALS算法,且具有更高的拟合精度.但当加载矩阵特别是已知矩阵中存在几乎共线性的列向量时,BALS算法仍需大量的迭代次数达到收敛.
为了提高PARAFAC模型的拟合速度,笔者在已有BALS算法的基础上,提出了一种新的PARAFAC模型拟合算法,即NBALS算法.笔者给出了所提算法中最优松弛因子对的求解方法,并分析了所提算法的计算复杂度,最后将所提算法应用于两跳多输入多输出(MIMO, multiple-inputmultiple-output)中继通信系统,仿真结果验证了所提算法的有效性.
1 PARAFAC模型三维PARAFAC模型的标量形式可表示为[5]

|
(1) |
其中: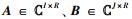

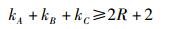
|
(2) |
其中:kA、kB和kC分别为A、B和C的Kruskal秩[2].式(1) 的3个剖面展开形式分别为
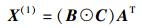
|
(3) |
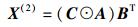
|
(4) |
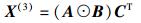
|
(5) |
其中: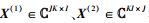

为了提高PARAFAC模型的拟合速度,所提NBALS算法利用新迭代与旧迭代之间的增量值,来预测下一次迭代的初始值.不失一般性,假设B已知,BALS算法的代价函数表示为[8]

|
(6) |
其中:‖·‖F表示Frobenius范数;

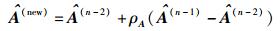
|
(7) |

|
(8) |
其中: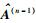
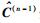






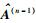
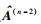
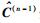
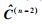
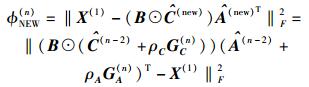
|
(9) |
定义T3、T2、T1和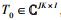

|
(10) |
为了表示方便,式(10) 省略了上标(n)和(n-2).式(10) 代入式(9) 可得

|
(11) |
其中:
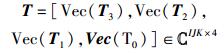
|
(12) |
Vec(·)表示向量化算子,如矩阵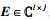
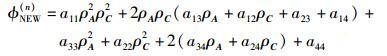
|
(13) |
定义一个复数矩阵
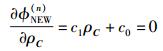
|
(14) |

|
(15) |
其中c1、c0、d1和d0的表达式为
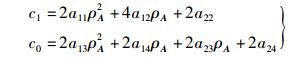
|
(16) |

|
(17) |
将ρC=-c0/c1代入式(15) 得
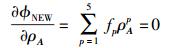
|
(18) |
其中实系数fp(p=1, 2, …, 5) 的表达式为
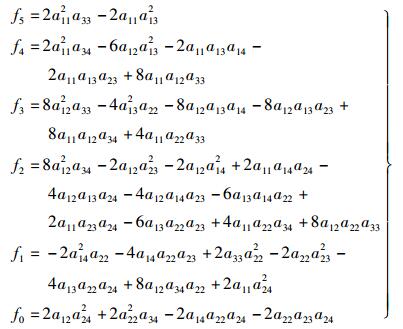
|
(19) |
求解式(18),得到5个根(ρA(u),u=1, 2, …, 5),选出其中的实根代入式(15) 求得对应的ρC,使得式(11) 最小的一组解(ρA, ρC)即为最优松弛因子对.
所提NBALS算法实现步骤如下.
步骤1 初始化
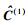
步骤2 n=n+1.
步骤3 ① 利用式(7) 与式(8) 计算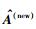
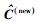
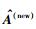
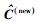
步骤4 利用B和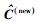

步骤5 利用
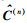
步骤6 重复步骤2~5,若满足判决条件|ϕNEW(n)-ϕNEW(n-1)| < ε(ε=10-5),迭代结束.
由于B已知,

使用复数乘法次数来分析算法复杂度.计算B⊙C需要JKR次乘法,采用SVD分解法求(B⊙C)†((·)†表示伪逆)需要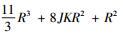
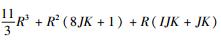
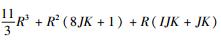
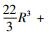
与BALS算法相比,NBALS算法增加的计算量主要在于计算Ti(i=1, 2, 3, 4) 和Q.计算T1、T2、T3和T4共需4IJKR+4JKR次乘法,计算对称矩阵Q需10IJK次乘法.因此,NBALS算法单次迭代约需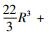
以一个具体数值为例,在图 4中,当I=4、J=3、K=4和R=4时,BALS算法单次迭代需要4 053次乘法,NBALS算法单次迭代需要5 493次乘法. BALS算法需要2 609次迭代才能达到收敛,NBALS算法只需要166次迭代就能达到收敛.那么,采用BALS算法拟合PARAFAC模型共需105 742 77次乘法,而采用NBALS算法拟合PARAFAC模型只需911 838次乘法,因此采用NBALS算法共节省了9 662 439次乘法.

|
图 4 不同训练序列块下,迭代次数对代价函数的影响 |
为了验证算法的性能,将NBALS算法应用于两跳MIMO中继系统进行信道估计,并与文献[8]中采用的BALS算法进行了比较(本算法的应用场景与文献[8]相同).根据文献[8]中式(21) 和式(22),目的节点接收的信号可建模为一个含有噪声的三维PARAFAC剖面模型:
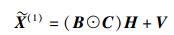
|
(20) |
其中: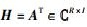
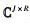
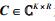
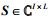

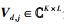
I为源节点总天线数,J为训练序列块的个数,K为目的节点总天线数,L为训练序列块的长度,R为中继节点总天线数.
假设信道H和信道C都为瑞利平坦衰落信道,信道H估计的性能由归一化均方误差(NMSE, normalizedmean-square error)表征,定义为[8]‖ 

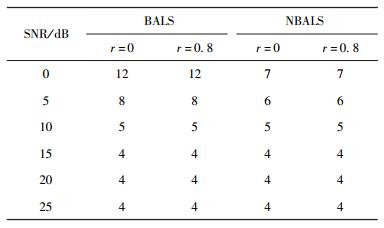
首先考虑B为通过离散傅里叶变换(DFT, discrete Fourier transform)生成的正交矩阵,训练序列块的个数J=4.定义一个相关矩阵Rr,其中[Rr]ij=r|i-j|,r为规范化相关系数.假设H=Rr1/2WRr1/2,C和W中的元素都服从均值为0、方差为1的独立复高斯分布. 表 1列出了不同相关系数下,BALS与NBALS算法所需的迭代次数.由表 1可知,与BALS算法相比,在低SNR条件下,NBALS算法需要较少的迭代次数.
|
|
表 1 不同相关系数下,2种算法所需的迭代次数 |
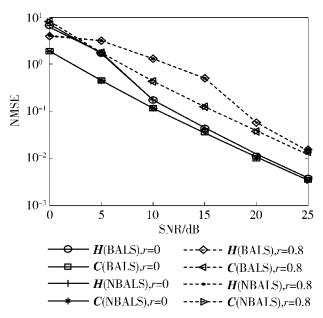
图 1所示为不同相关系数下,信道的NMSE.由图 1可知,无论采用BALS算法还是所提NBALS算法来拟合PARAFAC模型,都能有效地对信道H和C进行估计,并且2种算法所估计的信道都有近乎相同的NMSE性能.与r=0. 8(强相关)相比,r=0(不相关)时信道H和C都有着更好的NMSE.虽然只要K秩条件满足,且因子剖面不完全共线[1],BALS和NBALS都可以保证收敛,但是当加载矩阵中存在强相关列向量时,上述2种算法的拟合精度都会降低,从而影响信道估计的准确性.
|
图 1 不同相关系数下,信道的NMSE |
图 2所示为QPSK调制方式下,采用所提算法进行信道估计对系统误码率(BER, bit error rate)性能的影响. 图 2表明,信道不相关条件下,所提算法具有较好的BER性能.例如,在BER为10-2时,所提算法所需SNR约为20 dB,与理想信道(系统已知精确的信道状态信息)相比,所提算法只有2.4 dB左右的差距.

|
图 2 所提算法的BER性能 |
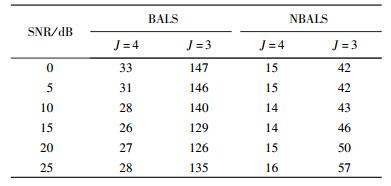
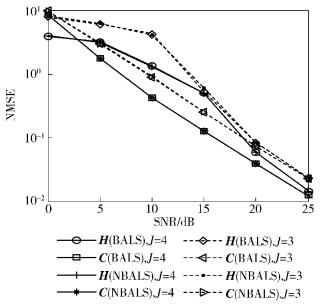
其次考虑B为随机生成矩阵,训练序列块的个数分别为J=4和J=3,不考虑相关信道(r=0). 表 2给出了不同训练序列块个数下,2种算法所需的迭代次数. 表 2显示,与BALS算法相比,NBALS算法明显地减少了迭代次数. 图 3所示为不同训练序列块个数下,信道的NMSE.由图 3可知,BALS算法和NBALS算法所估计的信道有着近乎相同的NMSE性能.与J=4相比,J=3时2种算法都需要更多的迭代次数,但是所估计的信道却具有较差的NMSE.这是因为在训练序列块数目变小的情况下,系统获取的信道相关信息变少,算法需要更多的迭代次数来拟合PARAFAC模型,但是拟合的精度仍低于前者.
|
|
表 2 不同训练序列块个数下,2种算法所需迭代次数 |
|
图 3 不同训练序列块个数下,信道的NMSE |
最后考虑B中存在几乎共线性相关列的情况,当训练序列块的个数为J=4和J=3时,不考虑相关信道,其他条件不变.当J=4和J=3时,B分别设为固定矩阵B4和B3:
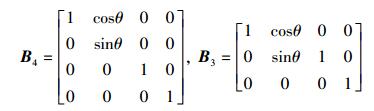
|
(21) |
B(B4或B3)中第1列和第2列的线性相关程度由θ决定,当θ=π/60时,B中第1列和第2列几乎共线. 图 4所示为不同训练序列块下,迭代次数对BALS算法和NBALS算法代价函数的影响(图中,θ=π/60,SNR为30).由图 4可知,当J=4时,BALS算法约需1 200次迭代达到收敛,而NBALS算法只需约60次迭代就能达到收敛;当J=3时,BALS算法约需2 600次迭代达到收敛,NBALS算法只需约170次迭代就能达到收敛.与已有BALS算法相比,所提NBALS算法所需的迭代次数几乎下降1个数量级.
5 结束语笔者提出了一种新的PARAFAC模型拟合算法,与已有BALS算法相比,当已知矩阵为正交矩阵时,所提算法虽然能减少迭代次数,但考虑其单次迭代的计算复杂度略高于BALS算法,所提算法不具备优势;当已知矩阵为随机矩阵时,所提算法大大地减少了迭代次数,所提算法优势明显;当已知矩阵中存在几乎共线性的列向量时,所提算法所需迭代次数几乎下降1个数量级,所提算法优势尤为明显.因此,在MIMO中继系统中,利用PARAFAC模型进行信道估计和信号检测时,当已知加载矩阵不满足正交条件时,所提算法具有其应用价值.
| [1] | Sidiropoulos N D, Giannakis G B, BroR. Blind PARAFAC receivers for DS-CDMA systems[J].IEEE Trans onSignal Processing, 2000, 48(3): 810–823. doi: 10.1109/78.824675 |
| [2] | Sidiropoulos N D, Bro R, Giannakis G B. Parallel factor analysis in sensor array processing[J].IEEE Trans on Signal Processing, 2000, 48(8): 2377–2388. doi: 10.1109/78.852018 |
| [3] | De Almeida A L F, Favier G. Raospace-time-frequency coding using semi-blind PARAFAC based receiver[J].IEEE Signal Processing Letters, 2013, 20(5): 471–474. doi: 10.1109/LSP.2013.2248149 |
| [4] | Bro R. Multi-way analysis in the food industry: models, algorithms, and applications[D]. The Netherlands: University of Amsterdam, 1998. |
| [5] | Rajih M, Comon P, Harshman R A. Enhanced line search: a novel method to accelerate PARAFAC[J].SIAM Journal on Matrix Analysis and Applications, 2008, 30(3): 1128–1147. doi: 10.1137/06065577 |
| [6] | Nion D, De Lathauwer L. An enhanced line search scheme for complex-valued tensor decompositionsapplication in DS-CDMA[J].Signal Processing, 2008, 88(3): 749–755. doi: 10.1016/j.sigpro.2007.07.024 |
| [7] | Chen Yannan, Han Deren, Qi Liqun. New ALS methods with extrapolating search directions and optimal step size for complex-valued tensordecompositions[J].IEEE Trans onSignal Processing, 2011, 59(12): 5888–5898. doi: 10.1109/TSP.2011.2164911 |
| [8] | Rong Yue, Khandaker M R A, Xiang Yong. Channel estimation of dual-hop MIMO relay system via parallel factor analysis[J].IEEE Trans on Wireless Comm, 2012, 11(6): 2224–2233. doi: 10.1109/TWC.2012.032712.111251 |