2. 北京邮电大学 计算机学院,北京 100876
针对视觉导引自动导引车的路径跟踪问题,提出了一种采用预测控制理论的分段控制模型.利用不等式约束对控制问题进行分段,提出以转弯半径为约束条件,解决了优化过程目标函数权重选择困难的问题.在每个控制阶段,采用单步预测方法找到最优的目标点,在输入约束和状态约束下用解析方法直接解出最优控制量,提高了解最优问题的速度.整个控制模型及方法目标明确,计算快速且计算量小,完全可以满足实时控制的需要,仿真结果证明了预测模型的有效性.
2. School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
A model of sectionalize control based on predictive control was presented for problems of vision-guided automated guided vehicle (AGV) path tracking. Control problems with inequality constraints were sectioned. The turning radius as constraint conditions was made, so that, the problem of the selection of objective function weights during the optimization process is solved. In each control period, a single-step prediction method was used to find the optimal target point, and obtain the optimal control variables directly by analytical methods under the input constraints and state constraints. The speed of the optimization problem is improved. This method fully meets the need of real-time controls, and it is used to calculate and small amount of computation. The validity of the model predictive is proved by the simulation results.
基于视觉导引的移动机器人极具发展潜力,近年来开始快速发展.路径跟踪是视觉导引自动导引车(AGV, automated guided vehicle)的核心技术,得到了国内外学者的广泛关注,是AGV研究的热点.
视觉导引一般通过车载摄像机获取局部视野中的指引信息,即AGV与路径标识线的相对偏差.大量的研究集中于几种常用的控制方法[1],如PID控制[2]、最优控制[3]、模糊控制[4]等. AGV是一个典型的时延、非线性不稳定系统,具有非完整性约束,上述传统方法在解决AGV的路径跟踪问题时控制参数整定困难,且难以处理客观存在的输入约束和状态约束.预测控制以系统模型为基础估计未来状态,从全局角度滚动优化整个控制过程,具有良好的可控性和鲁棒性.赵等[5]设计了一种两阶段的非线性预测控制器,解决了控制器终端镇定问题,但在解优化问题时无法避免参数选择的难题.武等[6]设计了一种智能预测控制模型,避免了参数选择的问题,取得了不错的控制效果,但在解优化问题时只能通过找到某一初值然后不断的迭代达到最优控制量,算法略显繁复.
提出了一种分段预测控制模型,根据控制目标的不同,将预测控制器分为3个阶段,各阶段的优化性能指标明确,并以解析方法直接得到了最优控制量,控制算法快捷简便.在最后一个阶段,设计了可同步消除所有偏差的预测控制算法,保证了控制器最终的稳定.
1 AGV运动学模型AGV在行驶过程中会产生2种偏差,即角度偏差和位置偏差.设k时刻,车体相对于路径标识线的角度偏差为eα(k),位置偏差为ed(k).设右轮线速度为VR,左轮线速度为VL,两驱动轮间距为Dw,则

|
AGV的线速度Vc和角速度ωc分别为
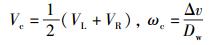
|
位置偏差分直线运动和圆弧运动2种情况.
1) 当两驱动轮之间的差速度Δv不为0时,AGV绕转动瞬心做圆弧运动,转动半径Ra为
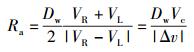
|
2) 当两驱动轮之间的差速度Δv为0时,AGV做直线运动.
得到AGV经过时间T的状态转移方程为
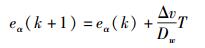
|
(1) |
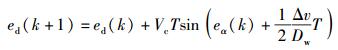
|
(2) |
当AGV的角度偏差与位置偏差满足一定关系时,如图 1所示,AGV可以同时消除2种偏差.

|
图 1 偏差同步消除模型 |
在路径上选择一点D为预定到达地点,D点满足|AC|=|AD|,D点即为最终的平衡点.由几何原理可知,当AGV沿CD弧行驶时,可以同步消除所有偏差,车体中心线与路径中心线完全重合.
转动半径Ra为
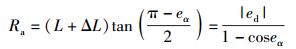
|
(3) |
AGV在任意瞬时都是绕车体做瞬心转动,则

|
即
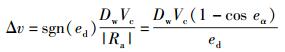
|
(4) |
式(4) 表明,当控制量一直为Δv时,AGV可驶向平衡点.
2.2 预测模型设计本研究以AGV当前偏差状态及AGV对平衡点的转动半径为依据,将控制过程分为3个阶段,第1阶段为纠偏阶段,第2阶段为过渡阶段,第3阶段为调节阶段.每一阶段依次向下一阶段转化,最终目标是进入第3阶段,并将AGV的偏差消除为零.据此,将AGV的偏差状态按不等式约束分成3个区域:偏离域、趋近域和终端域,分别对应3个控制阶段.
由AGV执行机构的限制,得到
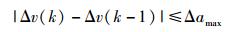
|
(5) |

|
(6) |
其中Δamax为控制变量的最大改变量,是对AGV机械性能的限制.式(5) 描述了对控制量的加速度限制,式(6) 描述了对控制量大小的极限限制.
以式(1)、式(2)、式(5)、式(6) 4个约束条件为基础,得到3个阶段优化控制问题的数学模型.
1) 第1阶段:纠偏阶段
纠偏阶段AGV向远离路径标识线的方向行驶,需快速扭转AGV的运动方向,优化的目标是以最快的速度将角度偏差减小到零并改变符号,得到如下的数学模型.

|
s.t. 式(1)、式(2)、式(5)、式(6)
终止条件:
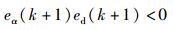
|
(7) |
当满足式(7) 时,控制系统进入下一阶段.
由J1可知,角度偏差为零时目标函数最小,得到AGV在纠偏阶段的控制量为

|
(8) |
当控制量不满足式(5) 时,将控制量修正为
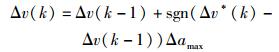
|
(9) |
2) 第2阶段:过渡阶段
过渡阶段AGV向路径标识线靠拢,但无法在平衡点同时消除2种偏差,需要调整AGV 2种偏差的关系,使AGV进入调节阶段.
首先引入终端域进入条件:
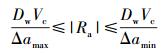
|
(10) |
其中Δamin为对AGV纠偏快速性的要求,可根据实际需求更改.满足式(10) 后,AGV可以进入终端域,Ra由式(3) 算出.当AGV在趋近域时,Ra的取值为以下2种情况:
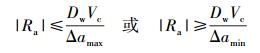
|
2种情况的目标不同,一种是尽快减小Ra;另一种是尽快增大Ra.该阶段AGV以偏差减小的趋势行驶,优化的目标是以最小的控制步数使AGV进入终端域,以第1种情况为例进行分析.

|
s.t. 式(1)、式(2)、式(5)、式(6)
终止条件:
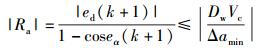
|
(11) |
当满足式(11) 时,控制系统可以进入下一阶段.
分析J2可知趋近终止条件的最优值为所求目标函数的极值
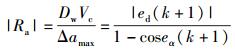
|
(12) |
将式(1)、式(2) 代入式(12),化简并求解,得到第1种情况的控制量为
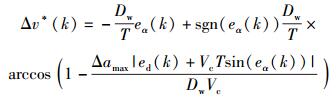
|
(13) |
同理得到第2种情况的控制量为
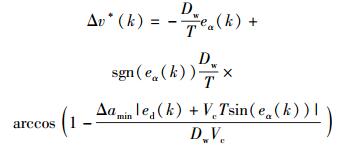
|
(14) |
当所得控制量不满足式(5) 的约束时,将控制量修正为式(9) 的形式.
3) 第3阶段:调节阶段
在AGV进入终端域后,系统趋近于平衡点,优化目标是使AGV在终端域内以最小的控制步数到达平衡点.

|
(15) |
s.t. 式(1)、式(2)、式(5)、式(6)、式(8)
式(15) 为终端域步数预测方程,表示在当前偏差状态,需要N步来消除偏差.
分析目标函数J3,对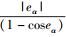
当AGV由Ra较大的方向进入终端域时,若预测控制步数满足需求,则直接用式(4) 得到控制量;若不满足需求,需控制AGV向Ra减小的方向行驶,得到控制量为
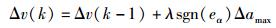
|
(16) |
其中λ为试探步长.由于在减小半径后的下一步控制需要将控制量变换到由式(4) 所确定的控制量,2个控制量必须满足式(5) 的约束,引入终止条件:
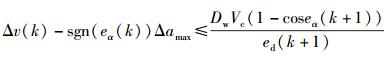
|
(17) |
当不满足式(17) 时,停止搜索,得到控制量,否则继续搜索.
综上,控制方案流程如图 2所示.
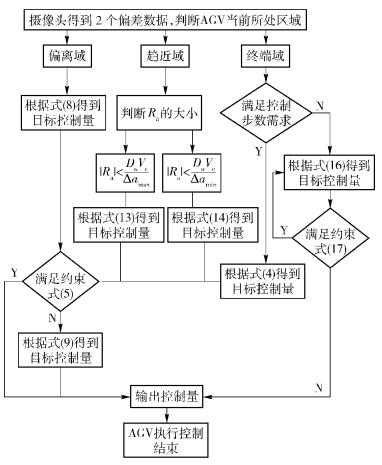
|
图 2 控制流程 |
为了验证分段预测控制模型的有效性,对各个控制阶段进行了仿真实验.系统初始参数设置为Vc=40 cm/s,Dw=28.5 cm,T=0.1 s,λ=0.1,Δamin=1 cm/s,Δamax=10 cm/s,Δvmax=30 cm/s.
1) 纠偏阶段的仿真如图 3(a)所示,初始角度偏差为15°,位置偏差为2 cm. AGV刚开始处于纠偏阶段,以纠正角度偏差为主,位置偏差增大,在0.5 s内进入过渡阶段;在过渡阶段2种偏差一起减小并在1 s左右进入调节阶段;调节阶段调用偏差同步消除算法,最终在2 s同时消除了2种偏差.
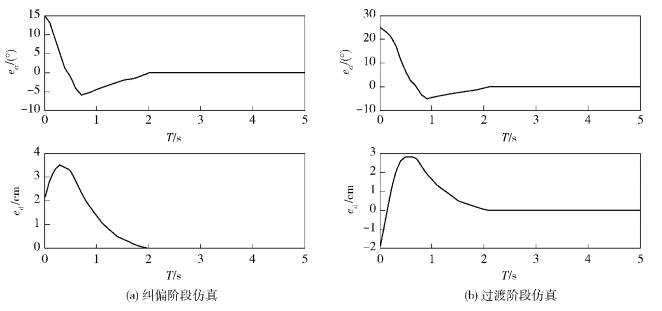
|
图 3 仿真结果 |
2) 过渡阶段某种情况的仿真如图 3(b)所示,初始角度偏差为25°,位置偏差为-2 cm. AGV刚开始处于过渡阶段,由于各种约束的限制,无法直接进入调节阶段,在纠偏过程中,位置偏差改变了符号并继续增大,0.7 s左右AGV进入了纠偏阶段,此后的过程与图 3(a)大致相同,在2 s时消除了偏差.
仿真结果表明,该分段预测模型在各个阶段控制策略清晰,纠偏速度可以满足实际需要,可平稳地消除2种偏差.
4 结束语利用分段控制思想将控制问题转化为多阶段决策问题,采用新的建模方法细分各个决策问题的约束条件和目标函数,并直接找到AGV的最佳目标点,简化了求解最优问题的计算过程.该方法结合了人工知识和代数优化的优点,且计算速度快,控制过程平稳,很好地解决了由AGV路径跟踪中的非线性和时滞性导致的控制难题,具有很好的实用价值.
| [1] |
艾青, 詹跃东, 王晓亮, 等. 视觉AGV差速转向控制方法研究[J]. 昆明理工大学学报:理工版, 2009, 34(2): 25–29.
Ai Qing, Zhan Yuedong, Wang Xiaoliang, et al. Control methods for AGV difference speed steering based on vision[J].Journal of Kunming University of Science and Technology: Science and Technology, 2009, 34(2): 25–29. |
| [2] |
李进, 陈无畏, 李碧春, 等. 自动导引车视觉导航的路径识别和跟踪控制[J]. 农业机械学报, 2008, 39(2): 20–24.
Li Jin, Chen Wuwei, Li Bichun, et al. Road recognition and tracking control of an vision guided AGV[J].Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(2): 20–24. |
| [3] |
王荣本, 储江伟, 冯炎, 等. 一种视觉导航的实用型AGV设计[J]. 机械工程学报, 2002, 38(11): 135–138.
Wang Rongben, Chu Jiangwei, Feng Yan, et al. Design for a new type of AGV based on machine vision[J].Journal of Mechanical Engineering, 2002, 38(11): 135–138. doi: 10.3321/j.issn:0577-6686.2002.11.029 |
| [4] |
张立明, 王振宇, 王翊, 等. 基于视觉的AGV两轮差速转向模糊控制[J]. 昆明理工大学学报:理工版, 2007, 32(4): 28–32.
Zhang Liming, Wang Zhenyu, Wang Yi, et al. Fuzzy control of a two-wheel difference speed steering AGV based on vision[J].Journal of Kunming University of Science and Technology: Science and Technology, 2007, 32(4): 28–32. |
| [5] |
赵韩, 尹晓红, 吴焱明. 非完整约束AGV轨迹跟踪的非线性预测控制[J]. 中国机械工程, 2011, 6: 681–686.
Zhao Han, Yin Xiaohong, Wu Yanming. A nonlinear, model predictive control of trajectory tracking for nonholonomic AGV[J].China Mechanical Engineering, 2011, 6: 681–686. |
| [6] |
武星, 楼佩煌, 杨雷. 基于视野状态分析的机器人路径跟踪智能预测控制[J]. 机器人, 2009, 4: 357–364.
Wu Xing, Lou Peihuang, Yang Lei. Intelligent predictive control based on state analysis of visual field for robot path tracking[J].Robot, 2009, 4: 357–364. doi: 10.3321/j.issn:1002-0446.2009.04.010 |


