2. 哈尔滨商业大学 计算机与信息工程学院,哈尔滨 150028
提出了一种基于Moran过程的接入网络选择方法,将选择策略的演化过程描述为有限个体间的群体博弈,并证明了每个群体策略演化是一个随机生灭过程.在此基础上,从多策略角度改进了局部更新机制,以揭示选择策略的演化机理.仿真实验结果表明,该方法能在有限演化次数内收敛到纳什均衡解,同时能避免无限群体博弈模型所产生的“乒乓效应”.
2. School of Computer and Information Engineering, Harbin University of Commerce, Harbin 150028, China
A new approach for multiple wireless networks access selection based on finite Moran process, namely access selection based on finite Moran process (ASFMP), was proposed, in which the process of selection strategy is described as a finite population game model, and each strategy evolution is proved to be a random birth-death process. The local update mechanism is then improved from a multi-strategy perspective, which is used to reveal the revolution mechanism of selection strategies. Simulation shows that the proposed method can convergence to Nash equilibrium within finite evolution times, and can also avoid the "Ping-Pong effect" caused by infinite population game.
B3G或4G移动通信系统提出了将所有无线接入技术进行整合,随时随地为移动用户选择最佳的接入网络和提供优质服务;在IEEE 802.21标准的支持下,移动终端可同时接入到多种网络实现并行业务传输,也可以根据业务需求在不同网络间切换.因此,如何在动态复杂的多网环境中选择最优的接入网络,已成为当前的热点研究问题.现有的接入网络选择方法主要分为以下2类.
1) 从多目标决策的角度研究接入网络选择问题[1-3],采用的决策参数涵盖主观指标和客观指标,如用户偏好、服务质量、能量消耗等,通过调整各个参数因子和约束条件将网络选择转化为单目标优化问题.这类方法充分挖掘促进网络优选的各种指标参数,却带来了较高的计算复杂度.
2) 从揭示选择过程的角度研究接入网络的选择策略及优化问题.这类方法用少量参数对网络选择过程进行博弈建模,典型的代表有文献[4]和文献[5].文献[4]从联合竞价的角度,将网络选择建模为一个Stackelberg博弈过程;文献[5]针对异构无线网络负载平衡问题,提出了一种基于群体博弈的用户网络关联方案,却没有对选择参数全局考虑,特别是基于群体博弈的选择方案建立于群体规模无限大、个体相互连接等假设上,与现实情况不符.
针对以上问题,笔者提出了一种基于Moran过程的接入选择方法(ASFMP, access selection based on finite Moran process),主要工作:① 从多参数决策的角度刻画接入网络选择的效用函数,作为后续群体博弈的收益函数,克服了现有方法中参数单一的局限;② 引入Moran过程,将网络选择过程描述为有限个体下的群体博弈;③ 通过仿真实验与对比分析,验证了算法的有效性.
1 无线网络接入问题的形式化描述设m个网络用X={1, 2, …, m}表示,S={1, 2, …, n}代表每个接入网络具有n个性能指标,sj表示第j个性能指标,如可用带宽、平均延迟、平均丢包率等.接入网络集合X对性能指标集合S的判决矩阵为A=(aij)m×n,其中aij(1≤i≤m, 1≤j≤n)∈[0,1]表示可用网络i对于性能指标sj的决策结果,或是网络i提供sj性能的概率(aij=1表示网络i可以提供100%的sj性能;aij=0表示不能提供sj性能).由于指标参数量纲不一致,因而需要对判决矩阵A进行标准化处理.对于效益型指标(如可用带宽)和成本型指标(如传输费用)的处理方法如式(1) 所示,数值越大,则指标越优.
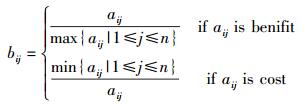
|
(1) |
因而得到标准化判决矩阵B为
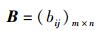
|
(2) |
假设存在q个移动终端,拟通过m个接入网络使用某种类型的网络服务,移动终端对n个网络资源的需求矩阵U为

|
(3) |
其中uij为终端i对网络性能sj的需求量.
由于各个度量参数在选择过程中的作用不同,所以采用信息熵来确定各个性能指标的权值.令P=(pij)m×n,其中
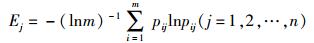
|
(4) |
当pij=0时,pijlnpij=0,偏差度dj=1-Ej,则性能指标sj的权值wj为
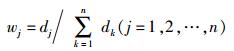
|
(5) |
因此,性能指标集的权值向量可表示为W(B)=(w1(b), w2(b), …, wn(b))T.如果移动节点未感知到备选网络k时,相应的权值wk(b)=0.该权重计算方法同样适合于用户资源需求矩阵U,需求矩阵U的权重向量可表示为W(U)=(w1(u), w2(u), …, wn(u))T.
在决策矩阵B和需求矩阵U的基础上,定义F为收益矩阵,采用移动终端对资源需求满足程度来度量,令F=(fij)q×m,元素fij计算如式(6) 所示.其中,∀l, wi(b)blj-wi(u)uil≥0说明如果有任何一项指标得不到满足,则对该网络资源的满意度为零.因此,fij越大,表明用户的满意度越高.如果没有合适的分配机制,移动终端总是选择满意度高的网络,致使其负载过高,性能迅速下降.同时,收益矩阵F中每个元素fij不是一个常量,任何接入策略的实施都可能引起F的变化,因此F必须周期性地更新.
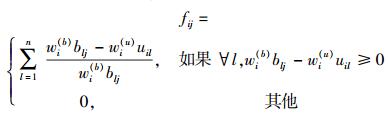
|
(6) |
终端用户的需求具有相似性,如看新闻、看视频等,同一类用户对网络资源的需求是等价的,也就是在矩阵F中存在元素fij=fi′j,移动终端i和i′对网j有着相同的资源需求,因此可以把移动终端i和i′划归到同一个子群中,意味着i和i′都可以采用接入网j的策略,据此可对总体进行分群.如果fij≤0,说明网j不能满足终端i的需求.如果不存在网络资源满足终端i的需求,则终端i就不参与本次资源分配,直到有满足条件的闲置资源出现.
q个终端在m个可用网络上的选择可看作是一个有限群体博弈,采用相同策略的终端可视为同一群体,因此每个个体均被划分到某一确定子群中;博弈过程采用异步演化策略,这种有限群体博弈的参与者、策略及演化过程可描述如下.
1) 参与者为所有移动终端:假设可用接入网络集合M中的用户终端数量为q,则用户终端集合表示为R={r1, r2, …, rq}.
2) 策略为终端对接入网络的选取:每个移动终端可选择的接入策略集合为Y=(y1, y2, …, ym), yx∈Y(x∈{1, 2, …, m})表示选择接入网络yx;每个移动终端均有|Y|=m个可选策略,但只能依概率选其一;经演化达到纳什均衡后,对每个用户而言获得的是一个纯策略,对每个子群也是一个纯策略平衡.
3) 策略演化为终端选取网络的规则:选取一个终端进行异步策略演化,也就是某一时刻的演化过程只针对单一个体进行,使整个网络服务处于一个相对稳定的状态.对于yx对应的群体Gyx而言,由于每次策略演化均会导致Gyx增加或减少一个个体(或保持不变).
从时间T=[0, ∞]上观察群体Gyx的变化.设过程{Gyx(t), t∈T}的状态空间为I={0, 1, …, q},总体中有‖Gyx‖个移动终端选择策略yx,在随机配对的情况下,则选择yx的平均收益为式(7);根据收益函数,移动终端集合Gyx继续选择使用yx演化的概率为式(8),使用yk≠yx演化的概率为式(9).

|
(7) |
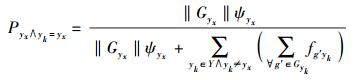
|
(8) |
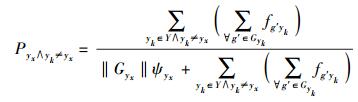
|
(9) |
其他策略群体Gyk(yk∈Y∧Gyk≠Gyx)中的个体采用yx进行演进的概率仍然是Pyk∧yx=yk.每步更新后,使用yx策略的终端数量‖Gyx‖有以下3种情况.
1) ‖Gyx‖增加一个个体,这是因为其他群体Gyk(yk∈Y∧Gyk≠Gyx)中有个体采用策略yx演化;
2) ‖Gyx‖减少一个个体,这是因为当前策略群体Gyx没有任何个体采用策略yx进行演化;
3) ‖Gyx‖保持不变,这是因为当前策略群体Gyx中有个体继续采用了策略yx进行演化.
使用策略yx的移动终端数‖Gyx‖可以用状态离散且状态空间为{0, 1, …, q}的Markov过程来描述,其转移概率为

|
(10) |
综上,这是一个时间连续状态离散的Markov生灭过程.
2.2 基于Moran过程的博弈策略演化机制为了避免网络选择的“乒乓效应”,借鉴Moran过程来实现策略异步演化.演化过程:在每一时间步中,从总体中随机选择1个个体,按其适应度的大小产生1个同类型后代,并替换总体中所选择的其他个体,总体数量保持不变;总体中只有1个个体复制且每次至多更新1个个体.但是这种策略选择需全局信息,该假设与现实情况不符.
笔者提出的移动终端博弈策略可采用局部更新机制.所谓局部更新,在每次策略演化时,随机选取1个个体与随机选取的另外1个个体进行收益比较,根据比较结果计算出此次演化所采用策略概率分布.文献[6]提出的局部更新是针对2种策略的选择,因此需要进行多策略演化的改进.
假定存在|Y|=m > 2个策略,已知个体a使用策略yx,对个体a进行策略更新时,需从其他m-1个群体Gyk(yk∈Y∧yk≠yx)随机选出m-1个个体组成集合N{b1, b2, …, bm-1};如果个体b∈N使用策略未知,那么个体a采用b策略的概率为

|
(11) |
其中: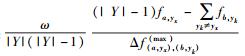
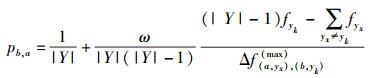
|
(12) |
当a和b的策略相互已知时,上述概率式(11) 和式(12) 分别转化为式(13) 和式(14),这与文献[6]的局部策略演进概率一致.
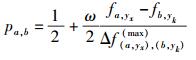
|
(13) |

|
(14) |
基于Moran过程的群体博弈算法ASFMP如下.该多策略演进方法本质上仍然是一个Moran过程,文献[6]证明了其纳什均衡的稳定性依赖于群体规模,通过Moran理论确知有限群体博弈的收敛性以及纳什均衡点的有效性.
算法1 Access Selection based on Finite Moran Process (ASFMP)
输入:任意移动用户的策略概率分布向量
输出:任意移动终端所使用的策略
1 计算决策矩阵B=(bij)m×n;//根据式(2),m个网络和n个判决需求
2 计算需求矩阵U=(uij)q×n;//根据式(3),q个终端对n个判决参量的需求
3 计算初始收益矩阵F=(fij)q×m;//根据式(6),q个移动终端能获得所需求资源的程度
4 进行分群;//将收益矩阵F中fij=fi′j所有的移动终端分为一个群体,可划分出m个群体
5 对每个群体的每个个体随机分配策略概率向量(py1, py2, …, pym);
6 计算每个群体的平局收益;//根据式(5)
7 对群体中每个个体计算出自身收益,对任何一个个体a,如果自身收益低于平均收益,开始异步更新过程;
8 从其他的m-1个群体中,每个群体中随机选取一个个体组成集合N={b1, b2, …, bm-1};
9 计算个体a,采用个体bi(i=1, 2, …, |Y|-1) 的当前策略的概率为pa, bi;//根据式(8)
10 按照概率pa, bi更新个体a策略概率向量;
11 判断每个个体是否为一个纯策略,如果所有个体为纯策略,执行步骤13;
12 否则,更新收益矩阵F,重新执行步骤6;
13 更新结束,输出每个个体的策略.
3 仿真分析场景及参数:在一个半径为100 m的圆形区域内,WLAN、WIMAX和UMTS 3种接入网络共存,忽略信号衰落带来的带宽衰减;但任何一种网络的接入延迟随接入终端数量的增加而呈指数级增长,根据容纳能力的不同,接入延迟为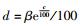
1) 视频服务,需求带宽为1 Mbit/s,允许的最大接入延迟为5 ms;
2) 数据服务,需求带宽为0.1 Mbit/s,允许的最大接入延迟为50 ms;
3) 音频服务,需求带宽为0.5 Mbit/s,允许的最大接入延迟为10 ms.
对总体为500的移动终端,随机分为3个群体,每个群体的个数不少于10,每个群体中使用3种策略(y1, y2, y3);演化前使用(0.0, 0.5, 0.5)、(0.0, 0.5, 0.5)、(0.0, 0.5, 0.5) 策略分配向量来置乱每个群体,然后再进行演化,结果如图 1所示.每个群体选择某一纯策略的概率为1的情况很难达到,因此设定当每个群体选择某一纯策略的概率超过0.9时,算法终止.由此可以看出,每个群体都能平稳地收敛到一个纯策略点,也就是纳什均衡点.在收敛过程中,同一群体中选择某个纯策略的概率逐步提高,说明这种局部更新机制能避免“乒乓效应”.
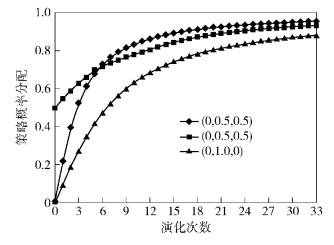
|
图 1 个体总数为500的策略分配概率 |
图 2为ASFMP和复制动态方程群体博弈算法(简称复制动态方程法)的对比情况.复制动态方程法在起始阶段有大量节点频繁切换接入网络,“乒乓效应”明显;ASFMP每次只有特定节点进行接入转换,在有效避免出现“兵乓效应”的同时,收敛速度在可以接受的范围内.由于“乒乓效应”会造成网络性能的严重下降,所以牺牲少量收敛速度来换取网络性能的稳定是值得的.

|
图 2 节点接入数量对比 |
群体平均收益变化情况如图 3所示. ASFMP的每次演化只是选择有限个体进行,收敛速度较复制动态方程法稍慢,然而后者的稳定性较差.在ASFMP中,演化策略导致群体规模发生变化,并最终引起平均收益发生波动,而其中个体并没有在收益波动中频繁切换接入策略.

|
图 3 ASFMP方法的收益变化 |
图 4为ASFMP和复制动态方程法的吞吐量对比情况.复制动态方程法在演化初期吞吐量波动较大,收敛速度较快;而ASFMP的系统吞吐量逐步提高,收敛速度略慢于复制动态方程法.随着演化次数的增加,ASFMP每个群体的收益逐渐达到上界,也就是纳什均衡点.当群体规模相对较大时,对单个群体而言,每次演化总是选择低于平均收益的节点与期望收益较高的节点进行,使每个群体的平均收益在演化过程中稳定上升,在演化初期上升速度较快,后期逐渐收敛到纳什均衡点.
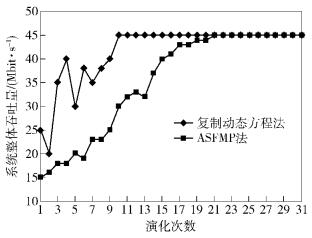
|
图 4 系统吞吐量对比 |
将多网选择问题抽象成有限群体博弈模型,引入Moran过程及改进的局部更新机制来揭示策略演化机理,克服了同步演化策略(如复制动态方程)所引起的“乒乓效应”,同时克服了传统算法中参数单一和全局假设问题,符合现实中移动终端的独立性和差异性现状.
| [1] | Kaleem F, Mehbodniya A, Islam A, et al. Dynamic target wireless network selection technique using fuzzy linguistic variables[J].China Communications, 2013, 10(1): 1–16. |
| [2] | Chamodrakas I, Martakos D. A utility-based fuzzy TOPSIS method for energy efficient network selection in heterogeneous wireless networks[J].Applied Soft Computing, 2012, 12(7): 1929–1938. doi: 10.1016/j.asoc.2012.04.016 |
| [3] | Farooq B, Victor C M L. Automated network selection in a heterogeneous wireless network environment[J].IEEE Network, 2007, 21(1): 34–40. doi: 10.1109/MNET.2007.314536 |
| [4] | Swamy C. The effectiveness of stackelberg strategies and tolls for network congestion games[J].ACM Transactions on Algorithms, 2012, 8(4): Art. No. 36. |
| [5] |
姜永, 胡博, 陈山枝. 异构无线网络用户网络关联优化:一种基于群体博弈的方法[J]. 计算机学报, 2012, 35(6): 1249–1261.
Jiang Yong, Hu Bo, Chen Shangzhi. User-network association optimization in heterogeneous wireless networks: a population game-based approach[J].Chinese Journal of Computers, 2012, 35(6): 1249–1261. |
| [6] | Traulsen A, Claussen J C, Hauert C. Coevolutionary dynamics: from finite to infinite populations[J].Physical Review Letters, 2005, 95(23): 1–4. |


