2. 伦敦大学 国王学院,伦敦 WC2R 2LS
邻接矩阵法可以对杆件的数目变化进行表示和演算,但这种方法对于变胞机构中复合铰链的构态变换及描述铰链的邻接关系变化的情况不完全适用,且矩阵所含信息较少,不能直观地反映机构构态特性.为此,应用邻接图表示机构的拓扑结构,并提出了描述机构详细信息的铰链邻接矩阵,此矩阵可与初等变换矩阵构造变胞方程,从而实现机构从初始构态到任意构态的矩阵演算.通过实例验证可知,基于邻接图的矩阵描述和演算方法获得的结果包含直观和全面的机构构态信息,便于计算机辅助分析.
2. King's College London, University of London, London WC2R 2LS, UK
Metamorphic mechanisms are widely studied and applied in theory and practice because of their characteristics of variable topological structures. The adjacency matrix is used in representation and operation of link changes. But this method is not available in configuration transformation with multiple joints and characteristics change of joints of metamorphic mechanisms, also the information of the matrix is poor. So it doesn't represent the configurations of metamorphic mechanisms intuitively. This article used adjacency graph to represent the topology of mechanism. The adjacency matrix of joint was proposed to represent the concrete information of the metamorphic mechanism. The metamorphic equation is constructed by multiplying elementary matrixes, and it is used to describe the transformations from one configuration to another. The verified examples indicate that the results obtained with the method have intuitive and comprehensive information of the configuration, and the method is easy to computer aided analysis.
传统的机构学理论基于固定的构件和运动副数目,因此有固定的自由度,而变胞机构[1]具有变拓扑的特性,能根据环境和工况要求进行自我重组和重构,因此具有多构态和多功能性,适用于不同的任务和场合. Dai等[2-3]讨论了变胞机构的构态变换及其矩阵演变.
邻接矩阵的表示方法基于拓扑图得出,其中行列均表示构件编号,利用初等变换实现邻接矩阵的改变.吴艳荣等[4]应用Huston低序体阵列描述变胞机构的拓扑结构.王德伦等[5]提出了一种符号邻接矩阵,用单位阵描述运动副的变化.李端玲等[6]提出了描述变胞过程中复合铰链情况的扩展关联矩阵,提出了用双色约束图表示运动链的拓扑结构[7].张忠海等[8]用位移子群表示运动链的拓扑结构.笔者所述方法对构态变换过程中任意杆件或铰链进行合并,得出简洁的矩阵表达式.该方法可实现:1) 描述杆件合并或铰链重合;2) 描述运动链中复合铰链和单铰链及其变换过程;3) 运动链的结构可通过矩阵直观得到;4) 通过计算机编程实现自动演算可得变换后任意构态的邻接关系.
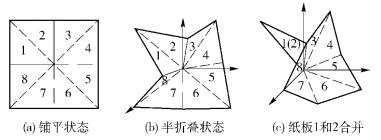
1 现有方法描述复合铰链变换及演变的局限性图 1所示为花样折纸的折叠过程,若将纸板当做刚性杆件,折痕当做铰链.由图 1(b)到图 1(c)为球面八杆机构的两杆合并后变为球面七杆机构的过程.其机构简图如图 2所示.
|
图 1 正四边形折叠纸板及其折叠过程 |
|
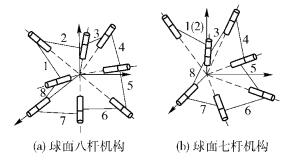
图 2 球面八杆机构向球面七杆机构演变的机构简图 |
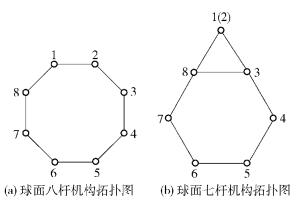
图 2中杆2折叠到杆1并与其合并用1(2) 表示,由图 2(b)可知,杆1(2)、杆3和杆8之间形成复合铰链.构态变换后的拓扑图如图 3(b)所示,应用戴建生等[3]所述构态变换方法可得邻接矩阵如式(1) 所示.
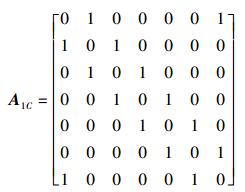
|
(1) |
|
图 3 球面八杆机构演变为球面七杆机构的拓扑图 |
式(1) 矩阵描述与纸板折叠后图 3(b)的拓扑图不符,实际杆1和杆2重合后,杆3和杆8铰接于杆1(2) 形成复合铰链.此种矩阵表示方法不能表示出复合铰链的信息,且需要对折叠后的杆件重新排序才能与矩阵对应.经分析,如图 1所示花样折纸的折叠过程不仅包含杆件合并,还包括铰链重合.之前的学者的研究都是基于拓扑图,只表示杆件之间的合并.对于铰链重合后铰链类型发生变化的情形不适用.
2 描述变胞机构的邻接图、铰链邻接矩阵及矩阵演算针对上述问题,笔者提出了邻接图表示和矩阵描述方法.首先定义杆件为作平面或空间运动的刚性体,且每个杆件至少有2个端点.分析发现,在开环或闭环运动链中,杆件的端点数目总是大于或等于杆件数.因此,用杆件端点的连接关系表示机构的拓扑变换能更全面地反应机构的拓扑结构.
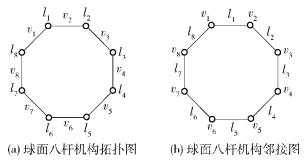
2.1 变胞机构的邻接图表示在邻接图中,顶点(○)表示杆件端点,线(—)表示杆件. 2个杆件连接于同一个顶点,则称此铰链为单铰链;3个及以上杆件连接于同一顶点称做复合铰链,用(◎)表示.杆件用lm顺序表示,顶点用vm顺序表示,这种表示机构的杆件顶点和杆件关系的方法即为邻接图. 图 4(a)所示为机构拓扑图;图 4(b)所示为机构邻接图.
|
图 4 球面八杆机构拓扑图和邻接图 |
铰链邻接矩阵与2.1节所述拓扑图的邻接矩阵表示不同.铰链邻接矩阵的行列用顶点符号vm表示;顶点重合用vi(vj1,vj2, …)表示;矩阵元素表示杆件,用符号lm表示,通过矩阵运算后的杆件重合用li+lj+…表示.一个运动链可以表示成s×s阶的方阵,如式(2) 所示.

|
(2) |
其中,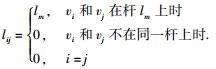
机构的拓扑变换有2种,即杆件的连接特性变化和杆件数目的变化[3].所述铰链邻接矩阵的矩阵元素为与铰链连接的杆件,所以演变过程为铰链的连接特性和铰链数目的变化.
矩阵演算中用到的2个矩阵:行变换矩阵用U表示,消去矩阵用E表示.
行变换矩阵U的表示方法:
U[vi(vj)]表示单位矩阵的vj行叠加到vi行;
U[vi1(vj1), vi2(vj2), …]表示多行同时叠加,叠加过程可用一个U矩阵表示.
消去矩阵E的表示方法:
E[(s-1)×s]表示消除其中的1行1列,得到(s-1)×(s-1) 阶方阵;
E(t×s)表示消除其中的(s-t)行和(s-t)列,得到t×t的方阵.
消去过程可以用一个矩阵表示,同时消去矩阵中vj1, vj2, …对应的行和列.
式(3) 在变胞方程中表示矩阵的第j行和第j列分别叠加到第i行和第i列;式(4) 表示消去矩阵的第j行和第j列.

|
(3) |

|
(4) |
变胞方程为B1=Et×sUi, jB0(Et×sUi, j)T,表示矩阵的行和列叠加及行和列消除后得到最终变换矩阵的过程,并用重合杆件表示B1对应杆件.
演算的规则为0+0=0, 1+0=1, 1+1=0.将演算规则及变胞方程用数学软件编程可直接得到从一种构态到另一种构态的铰链邻接矩阵.
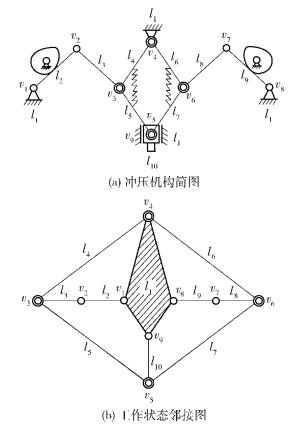
3 实例验证3.1 复合铰链的矩阵表示及矩阵演算图 5(a)为冲压机构简图,其对应的邻接图如图 5(b)所示.在工作状态,复合铰链v4和复合铰链v5处于分开状态,当处于恢复状态时,铰链v4和铰链v5重合得到新的复合铰链.此过程为两复合铰链重合为新复合铰链的情形.
|
图 5 冲压机构简图及工作状态邻接图 |
如图 5(a)所示机构的铰链邻接矩阵如式(5) 所示.

|
(5) |
冲压机构由工作状态到恢复状态的过程,杆件和铰链的拓扑演变描述为:铰链v4和铰链v5重合为v4(v5).
由此演变过程可得描述机构构态变换矩阵U和消去矩阵E,并将两矩阵代入变胞方程B1=Et×sUi, jB0(Et×sUi, j)T,得到如式(6) 所示矩阵形式:

|
(6) |
由变换后的邻接矩阵式(6) 可得,杆l4和杆l5重合,杆l6和杆l7重合;杆l1和杆l10重合,因此,矩阵元素l1用l1+l10代替表示重合杆件,如式(7) 所示.铰链v4(v5)为复合铰链.铰链v9为端铰链.恢复状态的邻接图如图 6所示.
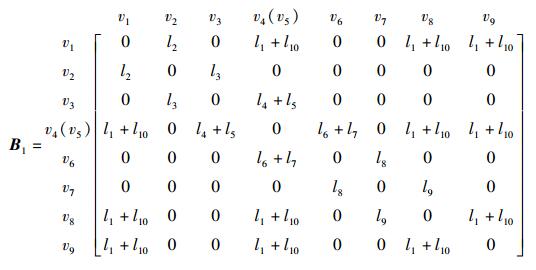
|
(7) |

|
图 6 修正后的恢复状态邻接图 |
提出的邻接图及其铰链邻接矩阵的描述与演算方法能描述含复合铰链的变胞机构的构态变换并且可以通过观察得出复合铰链位置.该方法不仅适用于变胞机构中杆件数目变化的描述及演算,而且适用于铰链数目变化的情形.应用邻接图和铰链邻接矩阵描述能更直观和全面地表示铰链和杆件邻接特性;变胞方程可以实现机构任意构态的矩阵演算,便于通过计算机编程演算;矩阵演算获得的铰链邻接矩阵与变换后的邻接图一一对应,并且可以对演变后的机构结构和性质进行预测和分析.
| [1] | Dai Jiansheng, Rees J J. Mobility in metamorphic mechanisms of foldable/erectable kinds[C/CD]//The 25th ASME Biennial Mechanisms and Robotics Conference. Baltimore, New York, 1998. New York: ASME, 1998: 375-382. |
| [2] | Dai Jiansheng, Zhang Qixian. Metamorphic mechanisms and their configuration models[J].Chinese Journal of Mechanical Engineering, 2000, 13(3): 212–218. doi: 10.3901/CJME.2000.03.212 |
| [3] |
戴建生, 丁希仑, 王德伦. 一空间变胞机构的拓扑结构变换和对应的矩阵演算[J]. 机械工程学报, 2005, 41(8): 30–34.
Dai Jiansheng, Ding Xilun, Wang Delun. Topological changes and the corresponding matrix operation of a spatial metamorphic mechanism[J].Chinese Journal of Mechanical Engineering, 2005, 41(8): 30–34. |
| [4] |
吴艳荣, 金国光, 李东福. 变胞机构的构态分析及其运动学仿真研究[J]. 机械科学与技术, 2006, 25(9): 1092–1095.
Wu Yanrong, Jin Guoguang, Li Dongfu. Research on configuration analysis and kinematic simulation of metamorphic mechanisms[J].Mechanical Science and Technology, 2006, 25(9): 1092–1095. |
| [5] |
王德伦, 戴建生. 变胞机构及其综合的理论基础[J]. 机械工程学报, 2007, 43(8): 32–41.
Wang Delun, Dai Jiansheng. Theoretical foundation of metamorphic mechanism and its synthesis[J].Chinese Journal of Mechanical Engineering, 2007, 43(8): 32–41. |
| [6] | Li Duanling, Zhang Zhonghai. Configuration analysis of metamorphic mechanisms based on extended adjacency matrix operations[J].Chinese Journal of Mechanical Engineering, 2011, 24: 1–7. doi: 10.3901/CJME.2011.01.001 |
| [7] | Li Duanling, Zhang Zhonghai, Mccarthy J M. A constraint graph representation of metamorphic linkages[J].Mechanism and Machine Theory, 2011, 46: 228–238. doi: 10.1016/j.mechmachtheory.2010.09.003 |
| [8] |
张忠海, 李端玲. 变胞机构结构变换的位移子群描述方法[J]. 北京邮电大学学报, 2013, 36(3): 44–48, 59.
Zhang Zhonghai, Li Duanling. Description of displacement subgroup for structure transformations of metamorphic mechanisms[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(3): 44–48, 59. |


