2. 中国电信股份有限公司北京研究院 市场研究部, 北京 100035
为了解决现有子空间聚类算法时间复杂度偏高和对输入参数敏感的问题,提出了一种基于联合熵矩阵的子空间聚类算法.通过计算每个属性实例分布的熵降维,计算任意两个维度的联合熵,形成联合熵矩阵,在联合熵矩阵中搜索最高阶全1子矩阵作为兴趣子空间,最后在兴趣子空间完成聚类.在人工数据集和公开数据集上的实验表明,与传统子空间聚类算法相比,新算法能以较低的开销识别维度更高的兴趣度子空间.
2. Department of Marketing Research, China Telecom Corporation Ltd Beijing Research Institute, Beijing 100035, China
Recent subspace clustering research results suffer from two problems: firstly, they typically scale exponentially with the data dimensionality or the subspace dimensionality of clusters. Secondly, present methods are often sensitive to input parameters. To overcome these limitations, a subspace clustering algorithm based on united entropy matrix (UEM) is presented. In the method, entropy is used to filter out redundant attributes and UEM is used to store united entropy of each two attributes. This method finds all interesting subspaces in UEM by searching all-one sub matrix. Finally, all subspace clusters can be gotten by clustering on interesting subspaces. The evaluation on both synthesis and real datasets show that our approach outperforms traditional subspace clustering methods and provides enhanced quality for finding subspace clusters with higher dimensions.
高维数据对传统的聚类分析技术是一项巨大的挑战.受维度灾难[1]的影响,任意两个实例之间的距离相差无几,传统的聚类算法中基于距离的度量方式将失去效用,有意义的簇往往仅存在于少数维度组成的低维子空间中.高维数据聚类的关键是搜索簇和它们所在的子空间.目前主流的方法可以分成3类:子空间搜索方法、基于相关性的聚类方法和双聚类方法.子空间聚类方法搜索存在于给定高维数据空间的子空间中的簇,其中子空间用整个空间中的维度子集来定义.
CLIQUE[2]算法是最早提出的子空间聚类算法,它采用类Apriori的机制探测所有可能存在簇的子空间. ENCLUS[3]是CLIQUE算法的改进. FINDIT[4]算法采用面向维的距离及维度投票的方式完成子空间聚类. EWSSC[5]算法利用模糊可扩展聚类策略,与熵加权软子空间聚类算法EWSC[6]相结合,提出了基于数据流的软子空间聚类算法. SSCC[7]算法发现线性相关的对象子集,分析不同的子空间投影以完成聚类.然而,现有的子空间聚类算法通常存在两方面的缺点:一是设定全局密度阈值造成了算法对参数敏感;二是大部分算法都无法准确识别包含交叠簇的数据集.
1 联合熵与密集子空间1.1 联合熵在信息技术领域,信息熵的概念得到广泛应用.在子空间中也存在一种能衡量实例在空间中分布均匀程度的“熵”.根据信息熵的定义,对一个m维空间D内存在的N个实例,其熵值可定义为

|
(1) |
其中:k为每个维度上均匀分箱的个数,一般k设置为10;ni为空间D中km个单元中第i个单元所包含的实例数量.当m=1时,对应由一个维度组成的单维子空间的熵,称为单维熵.当m=2时,代表 2个维度组成的2维子空间的熵,定义为2维联合熵.
熵作为衡量指标能有效地描述实例分布的均匀程度,当完全均匀时熵达到最大值,而完全不均匀时熵为0.基于该特性,可以通过熵值的高低来判定有意义的簇所在维度,进而找出子空间的位置. 3维及以上子空间上计算熵较为复杂,可行的方法是投影为更低维度的子空间,将兴趣子空间的存在信息映射到联合熵矩阵中,从而避免对高维子空间的直接处理.一般地,联合熵指2维联合熵.
相应地,空间D的联合熵矩阵可表示为式(2),矩阵中元素即D中某两个维度的联合熵.
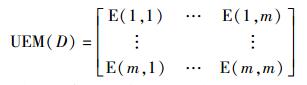
|
(2) |
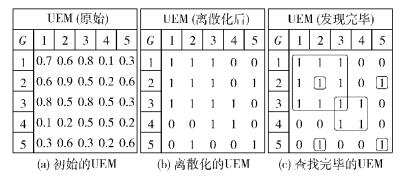
原始的联合熵矩阵必须离散化才能应用,即以矩阵所有非对角线元素平均值作为阀值,高于阀值则置为0,低于阈值置为1.然后,基于该矩阵进行兴趣度子空间即全1子矩阵的搜索.离散化和搜索过程如图 1所示.
|
图 1 联合熵矩阵的离散化和全1子矩阵 |
定义兴趣空间和非兴趣空间如下.
对于一个包含N个实例的空间D,当D中存在某个区域d满足式(3),则空间D被定义为兴趣空间.其中n是d包含的实例数,Vd和VD分别是d和D的超空间体积.一般地,α大于1.
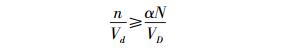
|
(3) |
而对于同样的D,如果D中所有的子区域都满足式(4),则空间D被定义为非兴趣空间.其中参数表意与式(3) 一致.基于式(3) 和式(4),提出并证明如下3个定理.
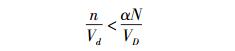
|
(4) |
定理1 一个非兴趣空间在其所有维度上的单维度投影子空间至少有1个是非兴趣空间.
证明 用反证法.假设标准化后的非兴趣空间D有m个维度和N个实例. D在第i个维度上的投影子空间P(D)i一定是兴趣空间.因为P(D)i是兴趣空间,由式(3),必然有1个包含ni个实例的区间[Ai, Bi]满足

|
(5) |
从1~m,将非负等式左右分别连乘,有式(6)~式(8),说明D内存在区域d满足式(3),D是兴趣空间,与假设矛盾.证毕.
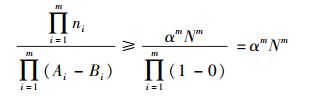
|
(6) |
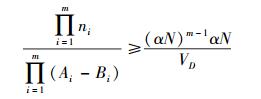
|
(7) |
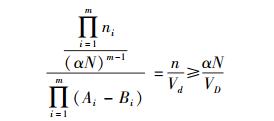
|
(8) |
定理2 一个兴趣空间的所有子空间都是兴趣空间(密集子空间的向下封闭性).
证明 用反证法.假设兴趣空间D有m个维度,存在有m个维度的非兴趣空间D是D的子空间.
由定理1,d在m个维度中的单维度投影P(d)i不可能都是兴趣空间,存在P(d)i (i∈{1,2,…,m})是非兴趣空间.由于d是D的子集,所以d的维度均是D的维度,维度i也属于D,同时D在第i维投影P(D)i是非兴趣空间.因为D在1个维度上投影是非兴趣空间,所以D内不可能存在任何区域满足式(3),D是非兴趣空间,与前提条件矛盾.证毕.
定理1证明了若存在全1子矩阵,则必然存在对应的兴趣子空间;定理2证明了若存在兴趣子空间,则必然表现为全1子矩阵;两者结合即证明全1子矩阵与兴趣子空间互为充要条件.
定理3 若1个空间的所有低1维度子空间都是兴趣空间,则该空间为兴趣空间(密集子空间的向上包络性).
证明 用反证法.假设存在非兴趣空间D有m个维度,且其m-1维的所有子空间Dm-1都是兴趣空间.因为D是非兴趣空间,由定理1,存在i∈{1,2,…,m},P(D)i是非兴趣空间.因为任意Dm-1是兴趣空间,所以P(Dm-1)i是兴趣空间.因为Dm-1是D的子空间,且Dm-1并集为D,所以i属于Dm-1中相对D缺失第i个维度的子集,由定理1可知,存在P(Dm-1)i是非兴趣空间.同时由定理2,因为Dm-1是兴趣空间,P(Dm-1)i是Dm-1的子空间,P(D)i是兴趣空间,产生矛盾.证毕.
定理3是CLIQUE和ENCLUS等自底向上方法的类Apriori策略能有效搜索兴趣子空间的理论基础.
2 子空间聚类算法UEMC2.1 问题描述子空间聚类问题可以描述如下:空间D包含m个维度和N个实例,如果D的子空间D内部存在簇C,且C在D内不能聚集成簇,则d称作兴趣子空间,在D内找到d的过程称为寻找兴趣子空间.而在已知的d内找到C的过程称为子空间聚类.由于聚类的方法较为丰富,子空间聚类问题的核心难点不在于聚类,而在于如何在D内找到所有满足条件的d.这有两方面的要求:第一是完整性;第二是简便性,即计算的复杂度不应太高.
2.2 算法步骤笔者提出一种基于联合熵矩阵的子空间聚类算法(UEMC,united entropy matrix clustering),步骤如下.
1) 过滤冗余维度.首先,利用实例分布熵来衡量1个维度内存在簇的可能性.一般地,划分等距单元格的参数k取10,而在第2) 步中计算联合熵的过程中,k相应取100.这一过程与ENCLUS基本一致,区别是采用平均值作为衡量冗余程度的阀值,不需要输入参数,避免了参数敏感带来的不利影响.当1个维度上实例分布在k个等距分箱内的数量差异形成的熵高于所有维度的平均值,则将该维度从候选维度列表中剔除.
2) 计算联合熵矩阵(UEM, united entropy matrix).对非冗余维度两两计算其联合熵形成联合熵矩阵.利用联合熵矩阵所有非对角线元素的平均值为阀值进行离散化,高于阀值为0,反之为1.
3) 查找全1子矩阵.因为对角线上的所有成员都是单维熵,必然小于联合熵而置为1,所以最小的全1子矩阵就是对角线上的单元素矩阵.对于元素Uii,如果有Uij=0(i≠j),则表示维度i与联合熵矩阵中其他维度没有关系,将{i}从联合熵矩阵中剔除.对于所有Uij=1(i≠j),由于Uii=Ujj=1,所以{i, j}是2维全1子矩阵.向更高维扩展的方法是:1个新的维度q能加入现有子空间{i, j}的充要条件是Uqr=1(r∈{i, j}).
4) 子空间聚类.找到全1子矩阵就意味着找到了兴趣子空间,因此最后一步是在兴趣子空间内聚类.并不限定某一种聚类算法,但建议使用基于密度的算法.
3 实验方法为了评估有效性,基于Java平台上实现了UEMC算法,并基于人工数据集和公开数据集进行了实验.评估标准分为两方面:一是完备性,即寻找兴趣子空间的结果;二是算法效率,即时间开销.
实验采用的人工数据集由随机数发生器在有偏置的条件下产生,包括10 000个实例,30个维度;10个簇,每个簇包含1 000个实例.公开数据集Plants(http://archive.ics.uci.edu/ml/datasets/Plants)来自加利福尼亚大学欧文分校(UCI,university of california irvine)Machine Learning Repository,包括34 781个实例和70个维度,每个实例是1种植物,69个有效维度代表有某植物生长的地理区域,其中美国53个,加拿大14个,丹麦、法国各1个.建模的研究目的是找出在这些地理区域内是否存在一些区域的组合空间,在该空间内植物的分布具有明显的聚集特征.
所有的实验都是基于同一台配置为2.5 GHz双核处理器、4 GB内存、320 GB硬盘的计算机.
4 实验结果4.1 找到兴趣子空间的能力表 1所示为人工数据集上的仿真结果.由于噪声点比例高达90%,4种算法均存在误判,既有漏掉维度,又有错误地分解子空间. UEMC在人工数据集上识别兴趣子空间的能力相比ENCLUS有7个更优、3个相等,相比FINDIT有5个更优、5个相等,相比SSCC有3个更优、5个相等和2个更劣. UEMC精度最高,SSCC其次,而ENCLUS最低.
|
|
表 1 人工数据集实验结果(“|”代表独立空间) |
表 2所示为在公开数据集上,UEMC搜索能力优于ENCLUS和SSCC,虽然FINDIT能搜索到14维子空间,但结果与其他3种自底向上的方法有明显差异.
|
|
表 2 公开数据集实验结果 |
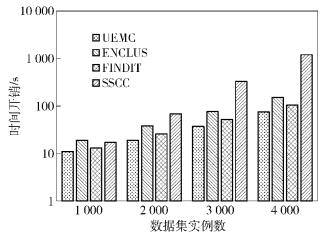
如图 2所示为不同算法针对维度数量的可伸缩性. UEMC与ENCLUS、FINDIT和SSCC类似,计算时间随着维度数增加呈线性增长. UEMC通过降维有效降低了计算量,因此时间开销更低.如图 3所示,UEMC、ENCLUS和FINDIT的计算时间随着实例数量的增加呈线性增加,而SSCC呈指数增长:由于UEMC仅扫描数据集1次,其时间开销低于FINDIT、ENCLUS和SSCC约10%~50%.
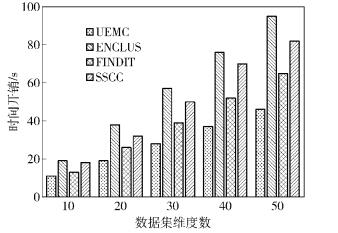
|
图 2 算法对维度的可伸缩性(实例数=1 000) |
|
图 3 算法对实例数的可伸缩性(维度数=10) |
在用联合熵计算求出的联合熵矩阵的基础上,提出了一种快速高效的子空间聚类算法.新方法将全空间的子空间检测转换为联合熵矩阵的子矩阵检测,节省了传统算法的多次迭代计算带来的时间开销.此外,算法不包含任何输入参数,解决了多数方法对输入参数取值敏感的问题.实验结果表明,新算法在寻找兴趣子空间的能力和时间开销上均有良好表现.下一步的工作重点是研究如何将高维数据的子空间聚类算法平滑移植到大数据环境下.
| [1] | Parsons L, Haque E, Liu H. Subspace clustering for high dimensional data: a review[J].ACM SIGKDD Explorations Newsletter, 2004, 6(1): 90–105. doi: 10.1145/1007730 |
| [2] | Agrawal R, Gehrke J, Gunopulos D, et al. Automatic subspace clustering of high dimensional data[J].Data Mining and Knowledge Discovery, 2005, 11(1): 5–33. doi: 10.1007/s10618-005-1396-1 |
| [3] | Cheng Chunhung, Fu Waichee, Zhang Yi. Entropy-based subspace clustering for mining numerical data[C]//Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM Press, 1999: 84-93. |
| [4] | Woo K G, Lee J H, Kim M H, et al. FINDIT: a fast and intelligent subspace clustering algorithm using dimension voting[J].Information and Software Technology, 2004, 46(4): 255–271. doi: 10.1016/j.infsof.2003.07.003 |
| [5] |
朱林, 雷景生, 毕忠勤, 等. 一种基于数据流的软子空间聚类算法[J]. 软件学报, 2013, 24(11): 2610–2627.
Zhu Lin, Lei Jingsheng, Bi Zhongqin, et al. Soft subspace clustering algorithm for streaming data[J].Journal of Software, 2013, 24(11): 2610–2627. |
| [6] | Jing Liping, Ng M K, Huang Joshuazhexue. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data[J].IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026–1041. doi: 10.1109/TKDE.2007.1048 |
| [8] | Stephan G, Ines F, Kittipat V, et al. Subspace correlation clustering: finding locally correlated dimensions in subspace projections of the data[C]//Proceedings of 18th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. Beijing: ACM Press, 2012: 352-360. |




