提出了一种考虑工艺变化下快速时序优化的缓冲器插入方法,该方法在布线区域内对线网结构进行图变换,把随机问题变为确定性问题,也就是把工艺变化下缓冲器插入时序优化问题等效成统计最短路径问题;同时,在构建图的过程中提出一种有效节点存储算法,将有效节点个数从指数级降为平方级,大大提高了存储和运行的效率.针对90 nm、65 nm和45 nm工艺下全局互连线缓冲器插入对本方法进行分析和验证,插入结果与已有方法的结果一致,证明了本方法的有效性;将该方法应用于直线线网和树型线网这两类集成电路中实际的互连线网,在分别插入17个缓冲器和3个缓冲器下达到了最优时序优化结果.
A buffer insertion method of a rapid timing optimization under process variation is proposed. The method carries out graph transformation on wire net in routing area, and so the random problem becomes a deterministic problem i.e. the buffer insertion problem for reducing time delay will be equivalent to statistics the shortest path problem. Moreover, we propose a valid node storage algorithm, which is optimized in constructing the graph process, and is greatly improving the memory space and working efficiency. In experiment section, the method is firstly used in 90 nm, 65 nm and 45 nm process global interconnect buffer insertion and analysis, and the insertion results are consistent with reference result, which confirms the validity of this method. Meanwhile, the algorithm was applied to two kinds of actual interconnect nets in integrated circuit: simple wire net and tree type wire net, which gets perfect timing optimization results based 17 inserted buffers and 3 inserted buffers respectively.
随着超大规模集成电路设计发展到超深亚微米阶段,连线的寄生效应不可忽略,互连线的时延在电路总时延中所占的比例不断增加,从而取代门的时延成为决定电路性能的主要因素.缓冲器插入优化技术是最为有效的减少互连线延时的方法.在解决缓冲器插入问题时,传统的方法要求相关电路参数为固定值,并且只能计算出插入缓冲器的个数,不能给出插入缓冲器的位置.但是,随着集成电路尺寸的不断变小,相关电路参数表现为随机性,参数的波动逐渐成为影响电路性能的重要指标.目前考虑工艺变化时缓冲器插入问题的研究主要分为两类:基于统计的方法;随机问题变为确定问题方法.
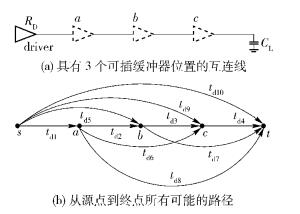
1 缓冲器插入问题的形式化及图表示1.1 缓冲器插入问题的形式化给定一个布线图G=(V, E),V表示节点,E表示两个节点之间的连接沿.两端线网源点s∈V,漏点t∈V;可行的缓冲器插入点a,b,…∈V.为了说明问题,只假定有3个可行的缓冲器插入点.求解布线图上一条从s到t的通路,特别地,该通路可以不经过任何缓冲器.优化目标,该通路的总延时最小,求最小缓冲器插入数目和位置.
1.2 缓冲器插入问题的图表示互连线上用插入缓冲器来减小延时,使互连线上的延时在给定约束条件或者称为成本函数下,达到最优化,即使成本函数最小.为了求出使成本函数最优化时缓冲器在互连线上的插入数目和位置,将缓冲器插入的位置等效为节点,将互连线等效为节点间的连接线,节点间的延时为该连接线的权重,这样缓冲器插入问题便等效为一个图的最短路径优化问题,如图 1所示.
|
图 1 缓冲器插入问题等效为图的最短路径问题示意图 |
随着集成电路尺寸的不断变小,器件参数的波动逐渐成为影响电路性能的重要指标[1],并带来大量的性能损失.因此,在考虑缓冲器插入延时时,延时是某依概率分布的随机变量,这样缓冲器插入模型中,图的边权重便不是固定值,这时的最短路径问题便成为统计最短路径问题.
2 统计最短路径的缓冲器插入算法2.1 图变换及有效节点存储算法因为缓冲器插入涉及有向图[2],设有向图G,需要找到从源点S到终点T的一条路径P,这条路径使得成本函数为最小,LP是它的长度,μP、σP2是它的均值和方差,成本函数为任意的函数.对于G中的任意沿e,设Xe为其分布函数,μe、σe2是它的均值和方差.所有沿的分布都假设为相互独立.对于2个独立的随机变量X和Y,若有Z=X+Y,则Z的均值和方差可以通过2个变量的均值和方差相加得到.但对于一般情况下的成本函数,并没有方差可以线性相加的性质.这需要找到一种新的方法来解决此问题,即统计最短路径问题.
Liang Deng等[1]提出了解决统计最短路径的算法,首先将G变换为G′,使G′是所有边沿具有固定权重参数的有向图,即边权重为延时均值μi,每个节点携带其到源点的某条路径的方差σP2.由此可以使用传统的算法找到G′中的最短路径.可以证明,G与G′中的路径是一一对应的,因而在G′中的最短路径对应G图中的路径,即为使成本函数最小化的最短路径[1].
但是遍历原图G所有路径随着节点数量的增多会呈2的指数倍增加,当节点个数为50时,这已经是1015数量级.因为G一定为有向无环图,可以将其节点进行拓扑排序.下面将介绍笔者提出的节点存储优化方法,这样可以有效节省存储空间和提高运算速度.
在创建G′图时,G图中每一个节点在G′中会裂变出多个节点,设G′中由G中同一节点分裂出来的为同一层,以互连线上具有50个等距离分布的候选缓冲器插入位置为例,并将源点到终点各个节点按次序分别编号为0~49.在G′中便有50层,G′中不同层的两点间延时和方差为其相应两层在G中对应的节点之间的延时和方差.若ui为G′中的一点,其下标i即为其到源点的路径总方差.例如,ui和vj间有连接弧,u和v分别代表不同层数,那么由文献[7]中的算法,则有j=i+σuv2,ui和vj间连接弧的权重为μuv.
减少存储的主要方法为在同一拓扑层使用合并相同方差节点的方法,即先判断某一层中vj点是否需要创建时,这样可以少创建很多的节点,节省相当多的存储空间而提高运算速度,这是因为:若不使用这种合并时,当创建第i层时,需要新创建的节点个数为前i-1层所包含的节点总数之和.即第0层创建1个点,第1层创建1个点,第2层创建2个点,第3层创建4个点,第i层时,需创建2i-1个点,若G中共50个节点时,在第49层需创建近1015数量级的节点.考虑到在G′中每一层创建点时,取决于已有节点和该层节点的方差,因为G′中裂点就是为了携带上方差的信息.这样,在第i层中会出现多少不同的总方差便只需创建多少节点.由于假设G中所有节点均匀分布,那么,在G′中两点间的均值和方差取决于两点所对应的层数差.例如,第0层中的节点和第2层的节点的方差与第1层中的节点和第3层的节点的方差一致.第0层中的节点和第1层的节点的方差与第2层中的节点和第3层的节点的方差一致.这样第3层节点方差中,从第0层→第1层→第3层,与第0层→第2层→第3层所在第3层产生的方差是一样的,那么这种情况的节点便可以合并.那么相当于,在创建第i层时,需要创建的节点个数,相当于i有多少种整数拆分,例如i=3时,3=1+1+1=1+2=3+0,这样第3层只需创建3个节点即可.需要新创建的节点个数和i的总的拆分数相同.由i的k拆分数公式[3]可得
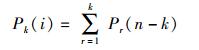
|
(1) |
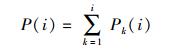
|
(2) |
假设G中有n个节点时,改进的图变化算法如下,此算法能有效的改善节点的存储空间.
创建第0层、第1层
for第2层至第n-1层
for G′中所有已创建的点ui
if i+σuv2不存在
创建新的vj,该点方差j= i+σuv2
ui和vj间插入弧,弧权重为μuv
else vj点已存在,ui和vj间插入弧,弧权重为μuv
创建终点t′,设为第n层
for第n-1层的所有节点ti
在ti和t′插入弧,弧权重为Φ(i)
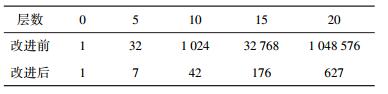
改进的图变换算法使节点合并后大大地减少了所需创建的节点个数,如表 1所示.而实际创建时,每层所需创建的节点个数可能要比改进后的还要少,这是因为可能会出现不同拆分情况下得到的总方差相同,不管如何,这种算法极大地节省了存储空间,提高了运算速度和效率.
|
|
表 1 不同层数节点个数对比 |
当将G ′图构建完毕后,问题便成为典型的最短路径问题,解决最短路径的算法有很多,如Dijkstra(迪杰斯特拉)算法、A*算法、SPFA算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法[4-5],笔者使用最经典的迪杰斯特拉算法来处理最短路径问题.迪杰斯特拉算法是典型的最短路径路算法,用于计算一个节点到其他所有节点的最短路径.主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止.迪杰斯特拉算法能找出最短路径的最优解.
将G ′图经过迪杰斯特拉算法处理后,便可得到最短路径的长度,但此时只能记录1条最短路径,当最短路径不止1条时,而不能记录所有的最短路径.为得到缓冲器插入的位置信息,必须将所有可能的路径都记录下来.
笔者提出一种新的方法能有效地记录所有最短路径和缓冲器插入的位置信息.本算法利用迪杰斯特拉算法在计算源点到终点的最短路径的长度时,数组dist记录了所有点到源点的最短路径长度.设源点为0,终点为t,dist[t]即为源点到终点的最短路径长度,由十字链表存储的特性可以很方便地找到与某点连接的所有点,以及其弧的信息即弧权重(设为μ).从终点t开始进行,遍历G ′图中的所有和t有连接弧的节点,如果节点μ满足式(3),则说明该节点在某条最短路径上.
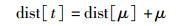
|
(3) |
若有多个节点满足式(3),则说明这些节点均在某条最短路径上,下一步将如遍历t节点一样遍历其他节点,直到遍历至源点结束.这样便生成了包含所有可能的最短路径上的节点,由它们在图中的连接关系反溯便可得到所有的最短路径,即能定位插入缓冲器的位置.
3 仿真实验首先对90 nm、65 nm和45 nm工艺下20 mm长全局互连线利用第2节提出的方法进行统计缓冲器插入分析;接着利用该方法对各个影响互连线缓冲器插入的电路参数进行了灵敏度分析;同时利用该算法对电路参数变化大小不同对缓冲器插入的影响进行了分析;最后将该方法应用于两类集成电路中实际的互连线网:直线线网和树型线网.笔者使用埃莫尔互连模型,在PentiumDual-Core E5300 PC上用标准C语言实现了该方法.
缓冲插入互连延时是由缓冲器的延时和互连线的延时2部分组成[1],故在考虑方差σ 2时,同样有2部分组成,即
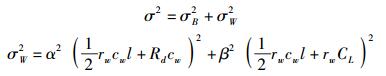
|
(4) |

|
(5) |
而参数α、β和θ为0.1~0.15的常数[1],其代表工艺参数有20%~30%的工艺变化,其他参数模型如图 2所示.
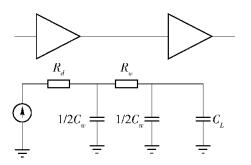
|
图 2 互连线的缓冲器插入参数模型 |
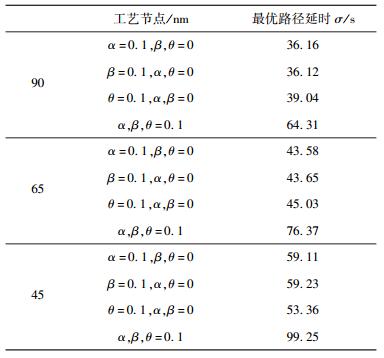
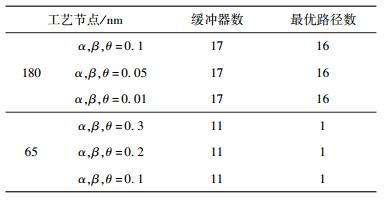
90 nm、65 nm和45 nm工艺下,相应的工艺参数来源于ITRS 2009[6].为了仿真的一致性,所有工艺下的α、β和θ取值都为0.1,在90 nm、65 nm和45 nm工艺下的仿真结果如图 3所示,互连线最优延时的均值和标准差都随着工艺尺寸的减小而增加,这与ITRS预测的结果相一致.不同工艺下,对于互连寄生电阻、电容和插入缓冲器电路参数变化造成互连延时的变化进行了灵敏度分析,结果如表 2所示.同时对180 nm和65 nm工艺下工艺变化大小不同对缓冲器插入影响进行了仿真分析,结果如表 3所示,从中可以看出工艺变化很大时,对于缓冲器插入个数也没有影响.进一步地,极限情况下利用固定电路参数值的传统缓冲器插入方法得到的结果和利用统计方法插入得到的结果相同,这与文献[1]中的结论一致,但最优路径的延时标准差越来越大,这对电路的时序分析影响越来越大,结果如表 4所示.
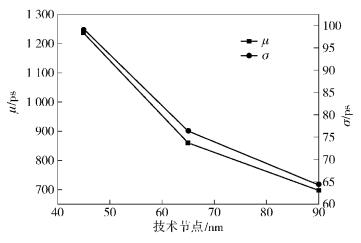
|
图 3 不同工艺下20 mm全局互连线统计延时分布 |
|
|
表 2 不同工艺下统计缓冲器插入情况 |
|
|
表 3 不同工艺变化情况对缓冲器插入影响结果 |
|
|
表 4 传统方法与统计方法插入缓冲器结果 |
最后把该方法应用于工业典型的180 nm工艺下2类线网,对于简单互连线网络缓冲器插入,当节点数为50时其输出结果如图 4所示.共有16条最短路径,每条最短路径上插入了17个缓冲器.插入缓冲器数目随线长的变化的关系曲线如图 5所示.从图 5可以明显看出,缓冲器插入的数目和线长呈近线性的关系,这种关系与固定参数的缓冲器插入类似,这同样说明在参数变化条件下,统计最短路径的缓冲器插入与固定参数最短路径缓冲器插入问题有很强的相似性.
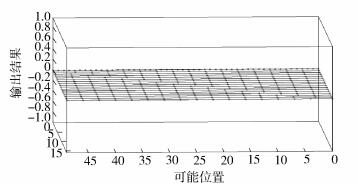
|
图 4 最内侧为50个可能位置的线,其余为16条缓冲器插入的最优路径 |
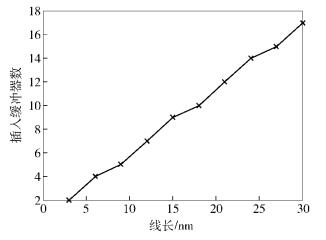
|
图 5 线长和插入缓冲器个数的关系 |
对于树型互连线的常见结构(见图 6),统计最短路径下缓冲器插入问题与一维简单线模型类似,最终将其等效为一维的问题加以解决.树型模型与一维模型的明显区别在于其图连接关系要比一维线模型复杂得多,具有多个终点,图 6中有4个终点T1、T2、T3和T4,其中每个拐点都是缓冲器候选插入点.同时每个节点的延时参数比一维情况下复杂得多,以图 6中节点4为例,从源点到节点4的延时计算为

|
(6) |

|
图 6 树型互连模型 |
对于图 6所示的树型互连结构,利用一维线模型的算法,计算出S-T1的最短路径结果,根据其缓冲器插入情况更新相应的延时参数.接着计算S-T2的最短路径结果,更新参数后,重新计算S-T1的最短路径结果.如此反复迭代,最终得到如图 7所示的树型互连线在统计最短路径下缓冲器插入位置信息,也就是共插入3个缓冲器.

|
图 7 最优缓冲器插入结果 |
提出一种考虑工艺变化下快速时序优化的缓冲器插入方法,该方法在布线区域内对线网结构进行图变换,把随机问题变为确定性问题.经过仿真实验,首先用90 nm、65 nm和45 nm工艺下全局互连线缓冲器插入实验,证实该方法的有效性;其次利用该算法对各个影响互连线缓冲器插入的电路参数进行了灵敏度分析,结果表明,90 nm互连线的寄生电阻变化对互连延时变化有很大影响,同时随着工艺尺寸变小互连电容变化对延时变化的影响越来越大;接着利用该算法对电路参数变化对缓冲器插入的影响进行分析认为,工艺变化对缓冲器插入个数和位置影响不大,但对互连时序有较大影响;最后将该方法应用于2类集成电路中实际的互连线网:直线线网和树型线网,得到比较好的时序优化结果,说明该方法可应用于集成电路布局布线后的时序优化和分析.
| [1] | Liang Deng, Martin D F W. An exact algorithm for the statistical shortest path problem [C]//Proceedings of the 2006 Asia and South Pacific Design Automation Conference, Yokohama, Japan, January 24-27. New York: IEEE, 2006: 965-970. |
| [2] | Gao Y, Wong D. A graph based algorithm for optimal buffer insertion under accurate delay models [C]//Proceedings of the Conference on Design, Automation and Test in Europe, Munich, Germany, March 12-16. New York: IEEE, 2001: 535-539. |
| [3] | 卢开澄, 卢华明. 组合数学[M]. 北京: 清华大学出版社, 2006: 70-80. |
| [4] | Elliott S C, Alan B P A, James J S. The stochastic shortest route problem[J].Oper Res, 1980, 28(5): 1122–1128. doi: 10.1287/opre.28.5.1122 |
| [5] | Frank H. Shortest path in probabilistic graphs[J].Oper Res, 1969, 17(4): 583–599. doi: 10.1287/opre.17.4.583 |
| [6] | International Technology Roadmap for Semiconductors[EB/OL].http://www.itrs.net.. |