2. 西安邮电大学 通信与信息工程学院, 西安 710061
为了利用垂直维度的空域资源进行三维波束赋形, 提高终端接收信号的信干噪比和系统容量以及系统能量效率, 实现绿色节能的通信, 对均匀平面阵列天线的三维波束赋形技术的基本原理进行了研究.波束在垂直方向的角度分辨率直接影响着垂直维度的空域资源利用率, 通过Matlab仿真分析了不同因素对垂直方向角度分辨率的影响.仿真结果表明, 水平角度对垂直方向的角度分辨率基本没有影响, 随着俯仰角的增大, 均匀平面阵在垂直方向的角度分辨率明显降低, 但可以通过增加阵元的数目提高垂直方向的角度分辨率, 实现对特定目标方向有效的三维波束赋形.
2. School of Telecommunications and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710061, China
3D-Beamforming is a promising technique for mobile wireless communication systems to improve the system performance and realize green communications. By exploring the vertical dimension of the spatial area, 3D-Beamforming could enhance the signal to interference plus noise ratio of the received signal, raise the spectrum utilization rate and improve the energy efficiency. The fundamental theory of array antenna's 3D-Beamforming is studied. The half-power beam width (HPBW)of the beam at vertical dimension has been computed by Matlab simulation under influence of different factor. Simulation shows that horizontal angular does not affect the basic level of HPBW, with the increase of vertical angular, the HPBW increase significantly, but it can be decreased by adding more antenna array unit.
波束赋形(beamforming)是智能天线[1]系统的一种关键技术,可以区分来自不同方向的信号,针对目标用户发送信号,提高目标用户的信噪比和系统能量利用效率,同时又能够减少对其他用户的干扰,降低系统干扰,提高小区边缘用户吞吐率和平均吞吐率,此外还能够利用相同的时频资源向不同位置的用户进行信号传输实现空分复用,充分利用空域资源从而提高频谱利用率和系统容量.
笔者研究了均匀平面阵列天线的三维波束赋形技术的基本原理,利用Matlab编程分析了水平角度、俯仰角及阵列数目等因素对垂直方向角度分辨率的影响并做了简要分析.通过改变不同的参数,绘制了不同因素对均匀平面阵的三维波束赋形效果图, 从中可以直观地感受不同因素对三维波束赋形效果的影响.
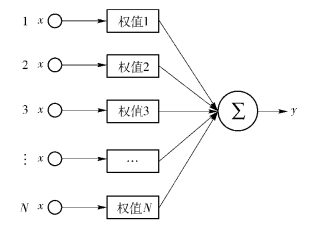
1 波束赋形基本原理实现波束赋形的最基本的方法是对各个天线阵元的信号进行适当延迟后相加,使目标方向的信号同相叠加得到增强,而其他方向均有不同程度的削弱,该方法通常用于模拟信号.数字信号可以通过对各个天线阵元的信号乘以复加权系数后相加,如图 1所示.加权系数不仅可以调整信号相位,而且可以调整信号幅度.对于窄带信号而言,不仅可以增强目标方向的信号,而且可以通过合理设置零点来抑制其他方向的干扰和噪声.
|
图 1 波束赋形基本原理图 |
目前,波束赋形的研究主要集中在二维波束赋形[2]的到达方向角(DoA,direction of arrival)估计及二维波束赋形权值的自适应算法研究. Akbari等[3]和Varade等[4]研究了基于多信号分类(MUSIC,multiple signal classification)算法和最小方差无畸变响应(MVDR,minimum variance distortionless response)算法的一维DoA估计. Sun等[5]介绍了基于最小均方误差(LMS,least mean square)算法和采样矩阵求逆(SMI,sample matrix inverse)的自适应波束赋形算法. Srar等[6-7]研究了基于RLMS(RLS-LMS)的自适应波束赋形算法,通过级联递归最小二乘法(RLS,recursive least square)和LMS网络来提高估计的准确度、收敛速度以及降低算法对信干噪比(SINR,signal to interference plus noise ratio)的依赖度.传统二维波束中垂直方向的天线下倾角是固定的,只是复用水平方向的空域资源,而三维波束赋形可以根据目标用户的位置,同时对水平和垂直方向的三维空间进行动态的波束赋形,提高了空域资源的利用率及频谱利用率.
二维波束赋形的相关研究已经非常成熟,然而目前关于三维波束赋形的研究较少. Saur等[8]通过设置几个不同固定下倾角的天线来覆盖整个小区,对不同区域的用户采用不同下倾角的天线来实现三维的波束赋形.通过调整下倾角可以在一定程度上提高系统性能,但是下倾角的调整很缓慢,很难针对移动的目标用户进行连续的波束赋形.真正意义上的动态三维波束赋形要能从根本上克服传统天线的不足,根据用户位置为每个用户产生具有不同下倾角的细窄波束.
三维波束赋形技术研究面临的主要问题有三维信道建模、三维天线设计、二维角度估计及自适应的三维波束赋形权值算法研究等.笔者重点研究水平角度、俯仰角及阵列数目等因素对垂直方向角度分辨率的影响,为保证有效的三维波束赋形提供了信号空间角度范围及天线数目等因素选择的参考.
2 阵列信号模型假设阵列信号是窄带信号,信号源位于阵列的远场,因此可以使用平面波传播理论,认为信号平行入射,各阵元接收到的信号之间没有幅度差异,只存在传播延迟造成的相位差异.
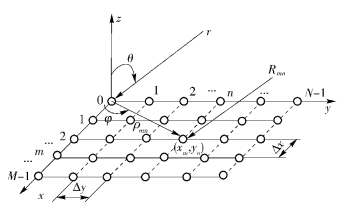
均匀平面天线阵是指天线单元按行、列等间距排列在一个平面内,若阵列的边界是一个圆,则为圆形平面阵,边界是一个矩形,则为矩形平面阵等.本研究主要讨论矩形网格矩形边界的平面阵,如图 2所示.阵列中各天线单元类型相同,尺寸相同,馈电幅度相等,天线单元间距分别为Δx、Δy,单元数分别为M和N.沿x和y方向排列的均匀直线阵的相位差分别为

|
(1a) |
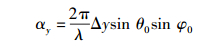
|
(1b) |
|
图 2 均匀平面阵的阵列信号模型 |
沿x和y方向排列的均匀直线阵的阵列响应矢量分别为
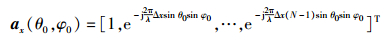
|
(2a) |
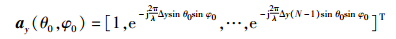
|
(2b) |
因此,均匀平面阵的阵列响应矢量为
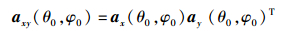
|
(3) |
均匀平面阵的方向图函数[10]为
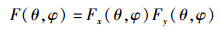
|
(4) |
其中,
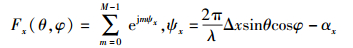
|
(5a) |
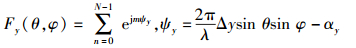
|
(5b) |
以上公式说明,矩形网格矩形边界的均匀平面阵总场方向图函数可以分解为沿x和y方向排列的均匀直线阵的方向图函数的乘积.由前面均匀直线阵的知识,可得平面阵归一化总场方向图函数为
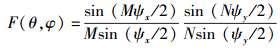
|
(6) |
空间角度分辨率[11]表示阵列天线对空间中不同角度的区分能力,对二维波束的角度分辨率通常用半功率波束宽度(HPBW,half-power beam width)的倒数来表示.垂直维度空间资源的利用主要受俯仰角的分辨率影响,下面通过仿真讨论垂直角度对三维波束赋形俯仰角分辨率的影响.
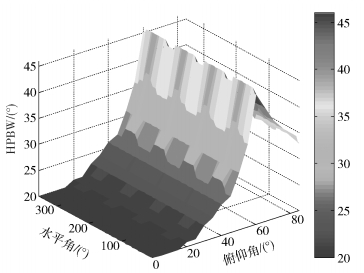
采用阵元数目为N=8、M=8,阵元间距为d=λ/2的均匀线阵天线,在水平及俯仰方向以5°为间隔角度向三维空间进行三维波束赋形,并计算各个方向俯仰角的HPBW.仿真结果如图 3所示.
|
图 3 半功率波束宽度变化图 |
由图 3可以看出,均匀平面阵垂直方向的分辨率受俯仰角变化的影响很大,基本不受水平角度变化的影响.在同一水平角处,当均匀平面阵俯仰角较小时,其HPBW基本保持不变,随着俯仰角的增大,其HPBW迅速增大,但当俯仰角增大到一定角度时,俯仰角的HPBW减小.这是由于在俯仰角增大的过程中,波束阵列的等效孔径在不断地减小,垂直方向波束主瓣逐渐不对称,主瓣俯仰角较大一侧的HPBW增加较快,当俯仰角增加到60°左右时,主瓣俯仰角较大的一侧与阵列天线平面相交,导致主瓣宽度计算不完全,因此表现出HPBW减小.在同一俯仰角处,均匀平面阵水平角的变化使俯仰角的HPBW有小幅波动,但基本保持不变.
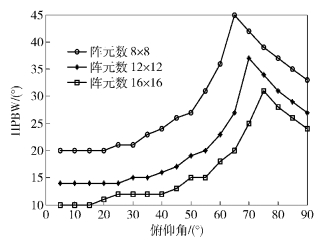
3.2 阵元数量对三维波束赋形的影响增大阵元数量可以提高阵列的等效孔径.下面通过仿真来验证不同阵元数目对俯仰角HPBW的影响,仿真结果如图 4所示.
|
图 4 阵元数目对俯仰角HPBW的影响 |
由图 4可以看出,随着阵元数的增加,俯仰角的HPBW不断减小,但两者并非呈线性关系变化.增加阵元数量能够增大阵元天线的等效阵列孔径,从而减小波束主瓣的半功率波束宽度,提高阵列天线的角度分辨率,但增加阵元数量就意味着更大的天线面积和成本增加.
不仅阵列数目会影响空间角度的分辨率,阵列的排列方式也会影响三维波束的空间分辨率.采用阵元数目为N=16、M=1,阵元间距为d=λ/2的均匀线阵天线,此时阵列天线为均匀线阵,向目标方向θ0=π/4, φ0=π/3发射一个窄带信号,得到如图 5所示的三维天线方向图.

|
图 5 均匀线阵的三维天线方向图 |
由图 5可以看出,均匀线阵在(θ0, φ0)方向的三维波束赋形结果是一个喇叭形的波束,而不是预期的指向(θ0, φ0)方向的定向波束,这并不是真正意义上三维波束赋形.这是因为直线排列的天线阵列只能分辨与天线排列方向的夹角,但不能分辨出三维空间的二维角度信息.均匀线阵所形成的喇叭状的三维波束实际上只是其二维波束以天线排列方向为轴进行旋转得到的,且其与天线排列方向的角度φ1与目标三维方向角度(θ0, φ0)的关系满足sin θ0cos φ0=cos φ1.由此可以看出,一维的均匀线阵并不能实现真正意义上的三维波束赋形,因此必须采用二维的天线阵列实现三维波束赋形.
3.3 三维波束赋形仿真采用x、y方向阵元数分别为M=8, N=8,阵元间距为dx=dy=λ/2的均匀平面阵,向目标方向θ0=π/4, φ0=π/3发射一个窄带信号,得到如图 6(a)所示的三维波束赋形效果图.
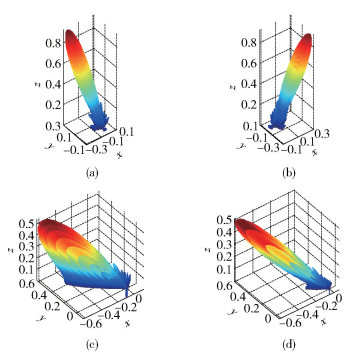
|
图 6 均匀平面阵的三维波束赋形效果图 |
为了检验相同阵元数目的均匀线在水平及垂直方向的赋形效果,保持阵元数目及垂直方向角度不变,改变水平方向的角度使φ0=-π/4,得到如图 6(b)的结果,由图可以看出,均匀线阵对水平方向不同角度的波束赋形效果相同.保持阵元数目及水平方向角度不变,改变垂直方向的角度使θ0=π/3,得到如图 6(c)的结果,可以看出,增大垂直方向的角度后,均匀线阵形成的三维棒状波束在垂直方向变宽,说明随着垂直角度的增加,均匀线阵对垂直方向角度的分辨率降低,导致垂直方向波束赋形效果变差.为了改善图 6(c)中的波束赋形效果,保持水平及垂直方向角度不变θ0=π/3, φ0=3π/4,增加天线阵元数目N=15, M=15,得到的结果如图 6(d)所示.结果表明,可以通过增加天线阵元数来弥补垂直方向大角度波束赋形效果不佳的问题.
4 结束语均匀平面阵垂直方向的分辨率基本不受水平角度变化的影响,但随着俯仰角增大而显著减小,可以通过增加阵元数目来增大垂直方向的分辨率.但当俯仰角增加到一定程度后,通过增加阵元数提高垂直方向角度分辨率的代价将成倍增长.一维的均匀线阵不能分辨三维空间的垂直和水平方向的角度,所以不能实现真正意义上的三维波束赋形.下一步将研究三维空间的多信源二维波达方向(DoA)估计或自适应的波束赋形算法,以实现多用户三维波束赋形,通过时域、频率、空域及功率等资源的联合调度提高系统资源利用率及能量效率.
| [1] | Nicolaescu I, Stoica D. Smart antennas for wireless communications systems[C]//ICECom, 2010 Conference Proceedings.[S.l.]: IEEE, 2010: 1-4. |
| [2] |
王曼珠, 张喆民, 崔红跃. MATLAB在天线方向图中的应用与研究[J]. 电气电子教学学报, 2004, 26(4): 24–27.
Wang Manzhu, Zhang Zhemin, Cui Hongyue. The application and study of antenna radiation pattern based on MATLAB[J].Journal of Electrical & Electronic Engineering Education, 2004, 26(4): 24–27. |
| [3] | Akbari F, Moghaddam S S, Vakili V T. MUSIC and MVDR DOA estimation algorithms with higher resolution and accuracy[C]//Telecommunications (IST), 2010 5th International Symposium on.[S.l.]: IEEE, 2010: 76-81. |
| [4] | Varade S W, Kulat K D. Robust algorithms for DOA estimation and adaptive beamforming for smart antenna application[C]//Emerging Trends in Engineering and Technology (ICETET), 2009 2nd International Conference on.[S.l.]: IEEE, 2009: 1195-1200. |
| [5] | Sun Yongjiang, Qiu Dongdong, Jin Huasong, et al. Research on adaptive beamforming algorithm[C]//Image Analysis and Signal Processing (IASP). 2012 International Conference on.[S.l.]: IEEE, 2012: 1-3. |
| [6] | Srar J A, Chung K S. Performance of RLMS algorithm in adaptive array beam forming[C]//Communication Systems, 2008. ICCS 2008. 11th IEEE Singapore International Conference on.[S.l.]: IEEE, 2008: 493-498. |
| [7] | Srar J A, Chung K S. RLMS algorithm for fixed or adaptive beamforming[C]//Communications (MICC). 2009 IEEE 9th Malaysia International Conference on.[S.l.]: IEEE, 2009: 163-167. |
| [8] | Saur S, Halbauer H. Exploring the vertical dimension of dynamic beam steering[C]//Multi-Carrier Systems & Solutions (MC-SS). 2011 8th International Workshop on.[S.l.]: IEEE, 2011: 1-5. |
| [9] | 卢万铮. 天线理论与技术[M]. 西安: 西安电子科技大学出版社, 2004. |
| [10] | Johson D H, Dudgeon D E. Array signal processing: concepts and techniques[M]. New Jersey: Prentice-Hall, 1993. |


