给出杨波等基于证书签名方案的一个伪造攻击, 攻击显示诚实但好奇的认证中心可在不知用户秘密值的情况下, 仅通过选取随机参数便能成功伪造任意用户对任意消息的有效签名.分析发现原方案不安全的原因在于证书生成阶段计算的承诺值R并没有作为签名阶段Hash函数的输入之一, 通过将R增加为Hash函数的输入, 给出了一个改进方案.改进方案在效率上与原方案是同等的, 在离散对数困难性假设下可证明是安全的.
A forgery attack on Yang bo et al.'s certificate-based signature scheme was presented. It is found that the "honest-but-curious" certificate authority could forge a valid signature in any message on behalf of any user by choosing random parameters without knowing the secret value of the user. Analysis describes that the reason of insecurity of the original scheme is that the commitment value R computed in the stage of certificate generation is not used as an input of the hash function in the stage of signature generation. An improved scheme was proposed by adding R to the hash function. The improved scheme is as efficient as the original scheme. It is provably secure under the intractability of discrete logarithm problem.
基于证书的密码体制作为一种新型公钥密码体制,结合了公钥基础设施和基于身份密码体制的优点,克服了其存在问题,从提出开始,就引起了广泛的关注,一系列利用双线性对的基于证书签名方案被相继提出.然而,运行一次双线性对运算所耗费的时间约为椭圆曲线上点乘运算的20倍,是目前较为复杂的密码操作.因此,为了提高效率,无对的基于证书签名对诸如无线传感器网络等能量受限的系统来讲就更具吸引力. 2008年,Liu等[1]首次提出了一个无对的基于证书签名方案,但是Liu等在其方案中附加一个关于私钥的知识证明来防止替换公钥攻击,导致方案的效率降低.随后,在2009年,Zhang[2]指出Liu等提出的方案不能抵抗Ⅰ型敌手AⅠ和Ⅱ型敌手AⅡ的攻击,并对其进行了改进,然而改进的方案仍然使用了对运算.同年,Yang等[3]也提出了无对的基于证书签名方案,而Li等[4]于2013年也指出Yang等的方案无法抵抗AⅡ的攻击,并给出改进的方案.
1 主要工作杨波等[5]于2012年利用离散对数问题(DLP, discrete logarithm problem)的困难性提出的基于证书签名方案具有很好的特性,比如方案没有使用映射到点特殊的Hash函数,其签名阶段只需要有限域上的2个加法和2个乘法运算,验证阶段也不需要复杂的双线性对运算,计算效率较高.杨波等[5]声称所提方案在最强的敌手模型中是安全的,可以抵抗超级AⅠ和超级AⅡ的伪造攻击.然而,当AⅠ替换用户的公钥后,必须向挑战者C提供被替换公钥所对应的秘密值才能获得可通过验证的消息签名对,否则无法证明C模拟的签名和真实签名不可区分,敌手可以不接受C返回的签名而导致模拟过程失败.另外,该签名方案实际上仍然无法抵抗AⅡ的攻击.具体来讲,一个超级敌手AⅡ是一个恶意但被动的认证中心(CA, certificate authority),该CA在系统初始化阶段就有预谋地针对预选用户设置含有陷门信息的系统参数,这种特殊的系统参数与正常系统参数是不可区分的,因此,相对于其他敌手,CA就拥有更大的优势来计算用户的私钥,进而伪造用户对任意消息的签名.然而,经分析发现,杨波等[5]的方案甚至不能抵抗一个普通敌手AⅡ的攻击,一个诚实但好奇的CA在得不到任何用户秘密值的情况下,仅通过选取随机参数以及多项式时间内的计算,便能以显著的概率成功伪造任意用户对任意消息的有效签名.笔者讨论了出现这种伪造攻击的原因,并针对原方案的缺陷进行了必要的改进,分析结果表明,改进后的方案在保留原方案计算效率高等优点的同时,有效克服了原方案的安全隐患.
2 对文献[5]方案的伪造攻击限于篇幅,杨波等[5]提出的方案不再赘述,下面给出一个诚实但好奇的CA对签名的伪造攻击过程,可证明该方案是不安全的.
1) CA随机选取u*∈Zq*,计算U*=gu*(mod p),h2*=H2(ID‖U*‖PKID‖M), h 3*=H3(ID‖U*‖PKID‖M).
2) CA计算R*=YID(-h*3/h2*),h1*=H1(R*‖YID‖ID),v*=u*+xh1*h2*,最后输出消息M的伪造签名σ*=(U*, v*, R*).
下面证明伪造签名σ*=(U*, v*, R*)是有效的.因为

|
即gv*=U*(R*Xh1*)h2*YIDh3*成立,这说明σ*=(U*, v*, R*)是用户ID在公钥YID下对消息M的有效签名,因此,杨波等[5]的方案无法抵抗普通的Ⅱ型敌手AⅡ的伪造攻击.
对原方案而言,在v=u+zIDh2+yIDh3中使用2个不同的Hash函数H2和H3是必要的.即使2个Hash函数的输入相同,但两者的输出是不同的,而且输出结果具有一定的随机性.若使用相同的Hash函数H,CA只需要计算U*=gu*U,h*=H(ID‖U*‖PKID‖M),然后计算v*=u*+zID(h*-h)+v,就能将σ*=(U*, v*, R)作为伪造的签名输出.很容易验证σ*也是用户ID在公钥YID下对消息M的有效签名.必须注意到,原方案在证书生成阶段计算的R=gr(mod p)并没有作为签名阶段的Hash函数H2和H3的输入,这是敌手能计算h2*、h3*和R*= YID(-h3*/h2*)进而伪造签名成功的原因,因此可以将R值绑定到H2和H3中来避免这种攻击.
3 改进方案及效率分析通过在签名阶段将杨波等[5]的方案在证书生成阶段计算的承诺值R增加为Hash函数的输入之一,提出了一个改进方案,改进方案的系统初始化及密钥生成算法与原方案相同,下面只给出其签名及验证算法.
1) Sign:用户ID随机选取u∈Zq*,计算U=gu(mod p),h2=H2(ID‖YID‖U‖R‖M),h3= H3(ID‖YID‖U‖R‖M),然后计算v=zID+(yIDh2+u)h3,最后将σ=(U, v, R)作为消息M的签名输出.
2) Verify:给定消息签名对(M, σ)、签名者ID的公钥YID,用户计算V=gv(mod p),h1=H1(R‖YID‖ID),h2=H2(ID‖YID‖U‖R‖M),h3=H3(ID‖YID‖U‖R‖M),最后验证V=RXh1(UYIDh2)h3是否成立.
由改进方案可以看出,若CA计算U*=gu*后将无法再计算h2*和h3*,因为此时R*尚未计算,CA也无法先计算R*=YID(-h3*/h2*),因为h2*和h3*的值与R*绑定,因此改进方案克服了对原方案的攻击.
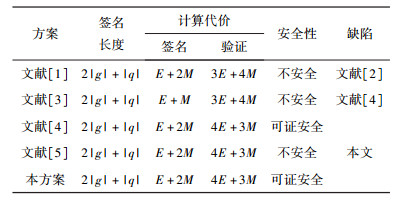
将目前已提出的无对的基于证书签名与改进方案进行比较,如表 1所示.其中,|g|表示Zp中元素的长度,|q|表示Zq中元素的长度,M和E分别表示Zp的乘法和指数操作.
|
|
表 1 方案比较分析 |
由表 1分析发现,改进方案无须花费额外的计算代价,保留了原方案计算复杂度低的优点,在签名长度和计算效率上是高效的基于证书签名方案.
4 安全性证明参考文献[4]中的证明技巧,下面分别给出改进方案对敌手AⅠ和AⅡ的不可伪造证明.
定理1 若存在一个Ⅰ型敌手AⅠ在T时间内,最多执行qHi(i=1, 2, 3) 次Hash询问、qcu次CreateUser询问、qusk次Corruption询问、qrpk次ReplacePublicKey询问、qcert次CertGen询问和qsign次Sign询问后,能以SuccCBSEF(AⅠ)的概率攻破所提基于证书签名方案,那么存在另外一个适应性选择消息和身份攻击的算法C,能利用AⅠ在期望时间T′≤(qcu+2qcert+4qsign)tex+2T内具优势AdvCBSEF(AⅠ)≥(1-1/qH1)qcert+qsignSuccCBSEF(AⅠ)/qH1来解决DLP的一个实例,其中tex为Zp上的一次指数运算耗时.
证明 假设C收到了DLP的一个随机实例(g, gμ),其目标是输出μ∈Zq*.为了利用AⅠ解决DLP,C需要模拟一个挑战者并回答AⅠ的所有询问. C首先置系统公钥为X=gμ并将系统参数params={p, q, g, X, H1, H2, H3}发送给AⅠ.其次,C随机选取IDk满足(1≤k≤qH1)作为游戏的挑战身份,其中qH1为可询问H1的最大次数.不失一般性,C需要维护5个初始为空的列表Lcu、LHi(i=1, 2, 3) 和Lcert.Lcu用来维护CreateUser、ReplacePublicKey和Corruption询问的记录,LHi(i=1, 2, 3) 用来维护Hash询问的记录, Lcert用来维护CertGen询问的记录.下面是C仿真挑战者与AⅠ的交互.
1) CreateUser询问:当AⅠ向C发布对IDi的公钥询问时,C查看Lcu列表,若存在{IDi, yIDi, YIDi},C返回YIDi给AⅠ;否则,C随机选取yIDi∈Zq*,计算YIDi=gyIDi并将YIDi返回给AⅠ.最后将{IDi, yIDi, YIDi}添加到Lcu列表.
2) Hash询问:当AⅠ向C进行Hi(i=1, 2, 3) 询问时,C分别随机选取αi、βi、λi∈Zq*为对应的Hi(i= 1, 2, 3) 值返回给AⅠ,并将对应值分别加入到LH1{Ri, YIDi, IDi, αi}、LH2{IDi, YIDi, Ui, Ri, Mi, βi}和LH3{IDi, YIDi, Ui, Ri, Mi, λi}列表.
3) ReplacePublicKey询问:当AⅠ向C发布对{IDi, Y′IDi}的询问时,C检查Lcu列表并将{IDi, yIDi, YIDi}改为{IDi, ⊥, Y′IDi}.
4) CertGen询问:当AⅠ向C发布对{IDi, zIDi, Ri}的询问时,C响应如下.
① 若i≠k,C随机选取zIDi、αi∈Zq*并计算Ri=gzIDiX-αi,然后检查LH1列表是否已存在{Ri, YIDi, IDi},若存在则需要重新选取zIDi和αi以防止碰撞. C将{Ri, YIDi, IDi, αi}和{IDi, zIDi, Ri, YIDi}分别添加到LH1和Lcert列表,最后返回{zIDi, Ri}给AⅠ.
② 若i=k,C终止.
5) Corruption询问:当AⅠ向C发布对IDi的秘密值询问时,C查看Lcu列表,若存在{IDi, yIDi, YIDi},C返回yIDi给AⅠ;否则,C随机选取yIDi∈Zq*,计算YIDi=gyIDi并将yIDi返回给AⅠ.最后将{IDi, yIDi, YIDi}添加到Lcu列表.
6) Sign询问:当AⅠ向C发布对{IDi, Mi}的签名询问时,C响应如下.
① 若i≠k且Lcu列表中存在{IDi, yIDi, YIDi}满足yIDi≠⊥,即公钥未被替换,则C首先查找Lcert列表中是否存在{IDi, zIDi, Ri, YIDi},若不存在则自己对{IDi, YIDi}分别进行CertGen和Corruption询问来产生{zIDi, yIDi},然后直接使用签名算法对消息M进行签名并将结果返回给AⅠ.
② 若i=k,或者i≠k且IDi对应的公钥YIDi被替换过,则AⅠ必须向C提供被替换公钥所对应的秘密值. C首先随机选取vi、αi、βi、λi∈Zq*,计算Ui= (gviYIDi-βiλi)λi-1和Ri=X-αi,然后置H1(Ri‖YIDi‖IDi)=αi,H2(IDi‖YIDi‖Ui‖Ri‖Mi)=βi,H3(IDi‖YIDi‖Ui‖Ri‖Mi)=λi.若Hi(i=1, 2, 3) 列表中已存在对应项,则需要重新选择αi、βi、λi以防止出现碰撞;否则,C将{Ri, YIDi, IDi, αi}、{IDi, YIDi, Ui, Ri, Mi, βi}和{IDi, YIDi, Ui, Ri, Mi, λi}添加到LHi(i=1, 2, 3) 并将(Ui, vi, Ri)返回给AⅠ.
假设C在模拟过程中不失败,AⅠ将至少以SuccCBSEF(AⅠ)的概率输出目标用户{ID*, YID*}对消息M*的有效伪造签名σ*=(U*, v*, R*),满足

|
(1) |
若ID*≠IDk,C将终止;否则,根据分叉引理,C通过输入{R, YID, ID}来重放AⅠ对H1的询问得到{R, YID, ID, α′}并将其添加到LH1列表.最后,C可在期望时间t=120 686qH1T/SuccCBSEF(AⅠ)输出一个新的有效签名σ′=(U*, v′, R*),满足
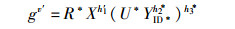
|
(2) |
这里需要注意的是,H2和H3的输出值h2*和h3*在C重放AⅠ对H1的询问前后保持不变.根据式(1) 和式(2),C最终输出μ=(v*-v′)/(h1*-h′1)作为DLP一个实例的解.若以下条件同时成立,C具优势AdvCBSEF(AⅠ)来求解DLP.
E1:C在整个模拟过程中不失败.
E2:AⅠ成功输出伪造签名σ*=(U*, v*, R*).
E3:若E2发生,在(ID*, σ*)中有ID*=IDk.
从上述仿真过程易知,C的成功概率AdvCBSEF(AⅠ)=Pr[E1∧E2∧E3].若AⅠ查询用户ID*的证书,由于C不知道μ值,因此C不发生终止的概率Pr[E1]≥(1-1/qH1)qcert+qsign;C在AⅠ输出一个有效的伪造签名而没有终止的概率Pr[E2|E1]=SuccCBSEF(AⅠ);若AⅠ不选择ID*作为伪造阶段的签名者,那么C也无法解决DLP,此事件不发生的概率Pr[E3|E1∧E2]≥1/qh1.下面计算AdvCBSEF(AⅠ)的下限.

|
C的运行时间等于它模拟安全性证明的时间与2倍的AⅠ的运行时间之和.在CreateUser、CertGen和Sign询问阶段,分别需要进行qcu、2qcert和4qsign次Zp上的指数运算,因此C的整个运行时间为T′≤(qcu+2qcert+4qsign)tex+2T,证毕.
定理2 若存在一个Ⅱ型敌手AⅡ在T时间内,最多执行qHi(i=1, 2, 3) 次Hash询问、qcu次CreateUser询问、qusk次Corruption询问、qrpk次ReplacePublicKey询问和qsign次Sign询问后,能以SuccCBSEF(AⅡ)的概率攻破所提基于证书签名方案,那么存在另外一个适应性选择消息和身份攻击的算法C,能利用AⅡ在期望时间T′≤(qcu+qusk+4qsign)tex+2T内具优势AdvCBSEF(AⅡ)≥(1-1/qH1)qusk+qrpk+qsignSuccCBSEF(AⅡ)/qH1来解决DLP的一个实例.
证明 与定理1证明过程类似,C首先随机选取x∈Zq*,然后置系统公钥为X=gx并将系统参数params={p, q, g, X, H1, H2, H3}和x一起发送给AⅡ.下面是C仿真挑战者与AⅡ的交互.
1) CreateUser询问:当AⅡ向C发布对IDi的公钥询问时,C查看Lcu列表,若有{IDi, yIDi, YIDi},C返回YIDi给AⅡ.否则,若i≠k,C随机选取YIDi∈Zq*,计算YIDi=gYIDi并将YIDi返回给AⅡ,同时将{IDi, yIDi, YIDi}添加到Lcu列表;若i=k,C直接置YIDi=gμ并将YIDi返回给AⅡ,同时将{IDi, ⊥, YIDi}添加到Lcu列表.
2) Hash询问:与定理1中的Hash询问回答类似.
3) Corruption询问:当AⅡ向C询问IDi的秘密值时,若i≠k,同定理1;若i=k,C终止.
4) ReplacePublicKey询问:当AⅡ向C发布对{IDi, Y′IDi}的询问时,若i=k,C终止;否则,C检查Lcu列表并将{IDi, yIDi, YIDi}改为{IDi, ⊥, Y′IDi}.
5) Sign询问:与定理1中的签名询问回答类似.
如果C在证明过程中不退出,AⅡ将至少以SuccCBSEF(AⅡ)的概率输出{ID*, YID*}对消息M*的有效伪造签名σ*=(U*, v*, R*),满足

|
(3) |
若ID*≠IDk,C将终止;否则,C通过输入{ID, YID, U, R, M}来重放AⅡ对H2的询问得到{ID, YID, U, R, M, β′}并将其添加到LH2列表.最后,C可在期望时间t=120 686qH2T/SuccCBSEF(AⅡ)输出一个新的有效签名σ′=(U*, v′, R*),满足
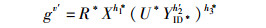
|
(4) |
这里需要注意的是,H1和H3的输出值h1*和h3*在C重放AⅡ对H2的询问前后保持不变.根据式(3) 和式(4),C最终输出μ=(v*-v′)/(h2*-h′2)h3*作为DLP一个实例的解.同理,C的成功概率为
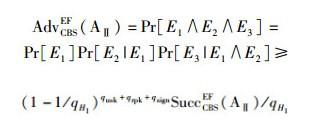
|
C的运行时间等于它模拟安全性证明的时间与2倍的AⅡ的运行时间之和.在CreateUser、Corruption和Sign询问阶段,分别需要进行qcu、qusk和4qsign次Zp上的指数运算,因此C的整个运行时间为T′≤(qcu+qusk+4qsign)tex+2T,证毕.
5 结束语首先指出了杨波等[5]所提的基于证书签名方案的安全缺陷,然后给出了一个改进方案,最后证明了改进方案的不可伪造性可归约到求解DLP.效率分析结果表明,改进方案是目前效率最高的基于证书签名方案之一,尤其适合计算能力及带宽受限的环境.如何构造在更强的敌手模型下的基于证书签名方案是一个公开问题,是下一步要努力的方向.
| [1] | Liu J K, Baek J, Susilo W, et al. Certificate-based signature scheme without pairings or random oracles[C]//ISC 2008. Berlin: Springer-Verlag, 2008: 285-297. |
| [2] | Zhang Jianhong. On the security of a certificate-based signature scheme and its improvement with pairings[C]//ISPEC 2009. Berlin: Springer-Verlag, 2009: 47-58. |
| [3] | Yang Ming, Wang Yumin. Efficient certificate-based signature scheme[C]//ISA 2009. Xi'an: IEEE, 2009: 87-90. |
| [4] | Li Jiguo, Wang Zhiwei, Zhang Yichen. Provably secure certificate-based signature scheme without pairings[J].Information Sciences, 2013, 233(6): 313–320. |
| [5] |
杨波, 肖自碧. 基于证书的签名方案[J]. 北京邮电大学学报, 2012, 35(5): 73–76.
Yang Bo, Xiao Zibi. Efficient certificate-based signature scheme[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(5): 73–76. |