针对多输入多输出-正交频分复用系统中最大似然检测算法难以硬件实现以及传统的信道估计性能较差等缺陷, 提出了一种联合估计检测算法.该算法使用离散傅里叶变换-最小二乘(DFT-LS)算法进行信道初估计, 利用广义空间迭代期望最大化(SAGE)算法对估计的信道信息进行校正, 并结合改进的粒子群优化(IPSO)算法完成对信号的迭代检测, 使系统性能得到改善.仿真分析结果表明, 算法能以较少的迭代次数估计出信道状态信息和检测数据; 在相同误比特率的情况下, 性能优于经典检测算法, 与理想状态下的最大似然检测算法仅相差1 dB左右.
The maximum likelihood detection algorithm for multiple input multiple output-orthogonal frequency division multiplexing (MIMO-OFDM) system is difficult to realize in hardware and the performance of traditional channel estimation is poor, in order to solve these problems, a joint estimation detection algorithm is proposed. To revise estimated channel using the discrete Fourier transform-least square algorithm for channel estimation and the space alternating generalized expectation maximization algorithm, the iterative signal detection is realized by combining the improved particle swarm optimization algorithm. Simulations show that the proposed algorithm can estimate the channel state information and detect data as well with less iteration number whose performance is much better than the traditional detection algorithm under the same bit error rate. There is only 1 dB difference between the bit error rate performance and the maximum likelihood detection algorithm under ideal channel.
在多输入多输出-正交频分复用(MIMO-OFDM,multiple input multiple output-orthogonal frequency division multiplexing)系统的接收端中,为了实现MIMO-OFDM系统的优良传输性能,对信道的精确估计和对信号的可靠有效检测是非常必要的[1-2].
近年来,联合半盲信道估计的检测技术因在信道状态信息不够准确的条件下具有优越性能而得到迅速发展[3]. Ylioinas等[4]提出了基于期望最大化算法的半盲信道估计算法,其利用算法的叠加信号处理思路来分离和估计出每个收发天线对之间的信道状态信息,然后通过迭代得到估计值,虽然该算法避免了矩阵求逆运算,但在每次迭代时需要更新整个参数集信息,其算法复杂度较高且对迭代初值要求较高.
目前,有效解决上述问题的研究不多,因此,提出了一种基于改进粒子群优化的联合信道估计检测算法,该算法通过联合内部粒子群优化迭代检测算法和广义空间迭代期望最大化(SAGE, space alternating generalized expectation maximization)算法迭代来更新信道状态信息和检测信息,提高了信号检测的可靠性.
1 系统模型MIMO-OFDM系统模型如图 1所示. MIMO-OFDM系统有NT根发射天线和NR根接收天线,假设信道最大多径时延路径数为L,OFDM符号的子载波数为K,在发射端,信源数据经信道编码后,进行串并转换分解成多个并行子数据流,每个子数据流进行映射编码,经过离散傅里叶变换后成为时域信号,并插入大于L的循环前缀(CP, cyclic prefix)以消除码间干扰,加入训练序列,再进行上变频,最后由多根发射天线同时发送出去.在接收端,通过下变频后提取训练序列信息进行信道初估计,然后去除时域信号的循环前缀并对其进行散傅里叶反变换,再经过联合估计检测处理,最终空时解码数据经信道解码后送至信宿,则第m根接收天线接收信息可以表示成
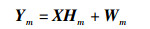
|
(1) |

|
图 1 MIMO-OFDM系统模型 |
其中:发送向量为X =[X1, X2, …, XNT],Xi=diag[Xi(0), Xi(1), …, Xi(K-1)],接收向量为Ym= [Ym(0), Ym(1), …, Ym(K-1)]T,噪声向量为W m=[Wm(0), Wm(1), …, Wm(K-1)] T,Hm是接收天线m的信道频域响应,Hm=[H1, m, H2, m, …, HNT, m]T,Hj, m是从发射天线j到接收天线m的信道频域响应,Hj, m=[Hj, m(0), Hj, m(1), …, Hj, m(L-1)] T,hj, m是从发射天线j到接收天线m的信道时域响应,hj, m=[hj, m(0), hj, m(1), …, hj, m(L-1)]T,hm是接收天线m的信道时域响应,h m=[h1, m, h2, m, …, hNT, m]T.
令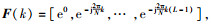
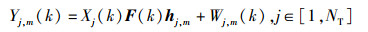
|
(2) |
则第m根接收的信号可表示为不同发射天线信号的叠加,即

|
(3) |
粒子群优化(PSO, particle swarm optimization)算法是随机产生一群粒子,并为每个粒子独立分配一对位置信息xi和速度信息vi,然后粒子利用设定的适应度函数评价出的粒子个体极值和全局极值,来改变粒子的速度与位置信息,通过迭代找到最优解[5].其中粒子群优化算法中粒子的速度和位置更新如下
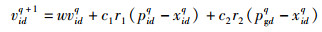
|
(4) |
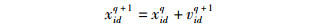
|
(5) |
其中:q为迭代搜索次数,d是维数,c1,c2为加速系数,r1和r2为(0, 1) 的随机数,vidq为在第q次迭代中粒子i的第d维速度,xidq为在第q次迭代中粒子i的第d维位置,pidq为在第q次迭代中粒子i个体极值点的第d维位置,pgdq为在第q次迭代中全局极值点的第d维位置,w为惯性权重,其用来控制历史速度对当前速度的影响.
3 联合估计检测过程3.1 联合估计检测联合估计检测是将OFDM解调数据进行信息提取,将接收到的训练序列数据经过离散傅里叶变换-最小二乘(DFT-LS,discrete Fourier transform-least square)估计输出初始信道估计信息,再经过SAGE算法的内部迭代环,当达到收敛条件时输出更新后的信道状态信息,然后将其提取的OFDM符号进行改进的粒子群优化(IPSO, improved particle swarm optimization)信号检测和SAGE算法内部迭代环处理,达到收敛条件时输出更新后的信道状态信息,最终经过IPSO检测输出检测数据信息,并将更新后的信道状态信息作为下一符号的初始信道估计信息.循环操作直至整帧数据检测操作完成.
3.2 训练序列的信道估计MIMO-OFDM系统在发送数据时,以帧为单位进行数据传输,在每帧帧头都存在一个训练符号子块,接收时系统将去掉保护间隔的OFDM符号经过OFDM解调后,将接收码符号分成n+1个子块,第1个子块为已知导频信息,其他子块为n个OFDM符号.根据每一帧前端已知的块状导频数据,对于接收信号基于LS的信道估计为
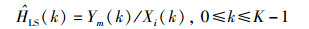
|
(6) |
去除信道估计中噪声对信道的影响,将大于循环前缀长度的估计值置零.将LS信道估计值进行离散傅里叶反变换得到

|
(7) |
其中IDFTK{·}是K点的离散傅里叶反变换.所有有用的信道信息都包括在前LCP个抽样点上,其余的抽样点都是纯粹噪声.因此只保留前LCP个抽样点,忽略噪声区间.其信道响应方程表示为
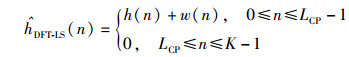
|
(8) |
进行离散傅里叶变换,从而得到DFT-LS信道估计为
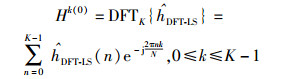
|
(9) |
其中DFTK{·}是K点的离散傅里叶变换.
3.3 SAGE迭代算法SAGE算法是通过潜在数据将不完全数据与待估计量之间建立对应关系,并在每次迭代估计中更新部分估计数据空间来简化处理[6].假设接收信号Y为不完全数据,发送数据X为潜在数据,h为待估计量,对于第k个子载波,在第m根接收天线上基于SAGE算法的信道估计如下
初始化,分别对j∈[1, NT],计算中间变量为
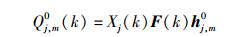
|
(10) |
当第r步迭代时,计算j=1+r modNT,得
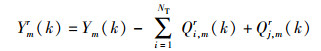
|
(11) |
然后更新计算信道冲激响应,得

|
(12) |
根据最小二乘准则,求解可得
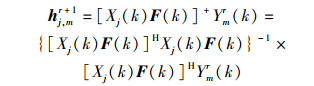
|
(13) |
由于系统为恒模调制,将式(13) 简化,可以得到更新后的第j个发射天线和第m个接收天线之间的信道冲激响应

|
(14) |
更新中间变量

|
(15) |
最后对于其他{i≠j}∩{i∈[1, NT]},有

|
(16) |
重复SAGE算法的操作,直到达到最大迭代次数时完成迭代过程,至此完成了第0个子块的信道状态信息跟踪,将其作为第1个子块的信道状态信息初值.
3.4 IPSO算法粒子群优化算法在迭代检测过程中,很容易陷入局部最优.本研究采用极值扰动机制当粒子群优化算法陷入局部极值后,通过调整粒子的个体极值和全局极值,使所有粒子从原区域迁移聚集到其他区域,经历新的搜索路径和领域搜索到全局极值的概率变大.极值扰动算子为
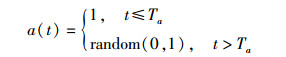
|
(17) |
其中Ta为停滞次数的阈值.对粒子群优化式(6) 和式(7) 添加极值扰动算子后得到
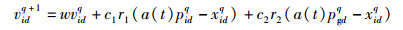
|
(18) |

|
(19) |
适应度函数是用来评估系统检测性能好坏的标准,针对MIMO-OFDM系统,根据式(1),利用最大似然估计可以得到检测信号为

|
(20) |
其中φ为MIMO-OFDM系统的所有可能发射信号向量空间.
取MIMO-OFDM信号检测的目标函数为
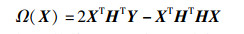
|
(21) |
由于目标函数值可正可负,为确保适应度函数的非负性,则信号检测中适应度函数修正为
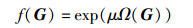
|
(22) |
其中μ为正常数,这里取0.1. MIMO-OFDM信号最佳检测问题可以利用粒子群优化算法通过适应度函数求解最优个体问题来解决.
在MIMO-OFDM系统中将需要检测出的符号信息作为目标,使用系统适应度函数计算出系统内各粒子与目标的距离,利用统计出的离目标最近粒子的位置和速度更新系统各粒子的位置和速度,使粒子向目标靠近,直至粒子移动到目标,检测出符号信息.粒子群优化算法与信号检测相结合,具体检测步骤如下:
步骤1 粒子群初始化,设置最大迭代次数为Q,粒子种群个数为N,在D维空间随机产生各粒子的位置信息xi0和速度信息vi0;
步骤2 根据式(22),通过适应度函数计算每个粒子在所对应位置处的评价值fi;
步骤3 将当前各粒子的对应位置处的评价值与本身存储的个体极值piq-1的评价值相比较,将最优值对应粒子的位置存储于个体极值piq;
步骤4 将更新后的各粒子个体极值的评价值与全局极值pgq-1的评价值相比较,将最优值对应粒子的位置信息存储于全局极值pgq;
步骤5 根据极值扰动机制在粒子群中选取适应度函数值较优的N/2个粒子,根据式(18) 和式(19) 更新每个粒子的速度viq+1和位置xiq+1,其他粒子按照式(4) 和式(5) 更新每个粒子的速度和位置,保持各粒子个体极值piq和全局极值pgq不变;
步骤6 当达到设定的迭代次数时停止搜索检测,粒子的全局极值点对应的位置信息即为检测出的数据信号,否则跳回步骤2执行.
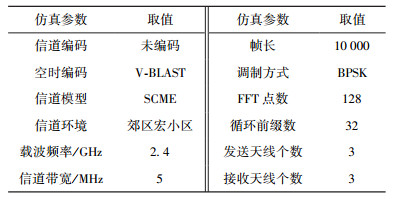
4 仿真结果与分析对所提出的SAGE-IPSO联合估计检测算法设计方案进行系统性能仿真,仿真参数如表 1所示.假设发送天线和接收天线都相互独立,并且1帧内信道参数基本保持不变,分别对系统检测的误比特率进行对比.
|
|
表 1 仿真参数 |
图 2所示为在参数如表 1所示的理想信道情况下,IPSO检测算法误比特率随IPSO种群个数和IPSO内迭代次数变化的性能曲线.仿真结果表明,随着IPSO种群个数和内迭代次数的增加,系统的误比特率有了显著的下降,其中种群个数和内迭代次数小于15的IPSO算法所取得的性能增益最为明显.其检测技术在种群个数和内迭代次数都取20后,算法基本趋于收敛,因此在实际中考虑到系统的复杂度,分别选取IPSO检测算法的种群个数和内迭代次数为15.

|
图 2 种群个数和内迭代次数对IPSO算法性能的影响 |
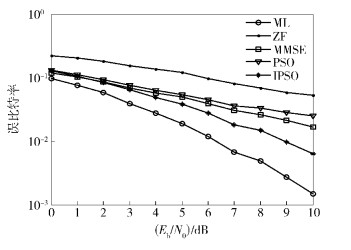
图 3给出了最大似然(ML,maximum likelihood)检测算法、迫零检测算法、最小均方误差(MMSE,minimum mean squared error)检测算法以及种群个数和内迭代次数选取为15的粒子群优化检测算法和笔者提出的改进粒子群优化检测算法,在仿真参数如表 1的理想信道情况下,不同信噪比的误比特率性能曲线.仿真结果表明,随着信噪比的增加,所有检测算法的误比特率都随之显著下降.在相同信噪比的情况下,所提的改进粒子群优化检测算法与传统的迫零检测和最小均方误差检测算法相比,其性能有了明显改善,算法与经典的ML检测算法相比,误比特率相差不大.
|
图 3 理想信道情况下的误比特率曲线 |
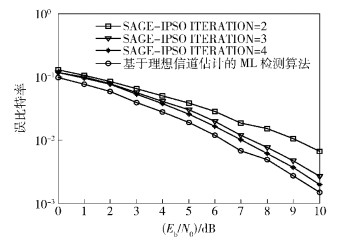
图 4为在IPSO检测算法的种群个数和内迭代次数选取为15,仿真参数如表 1的情况下,SAGE-IPSO算法误比特率随SAGE算法外迭代次数的变化曲线.仿真结果表明,随着迭代次数的增加,系统的误比特率有了明显的改善,其中前3次迭代所取得的性能增益最为显著. SAGE算法外迭代检测技术在4次迭代后,算法基本趋于收敛.因此在实际中考虑到系统的复杂度,选取SAGE算法外迭代次数为3.
|
图 4 外迭代次数对SAGE-IPSO算法误比特率性能的影响 |
图 5给出了基于理想信道估计的ML检测算法、基于LS信道估计的ML检测算法、基于MMSE信道估计的ML检测算法和笔者提出的SAGE-IPSO联合估计检测算法,在设定的仿真参数为表 1的情况下不同信噪比的误比特率性能曲线,其中IPSO检测算法的种群个数和内迭代次数选取为15,SAGE算法外迭代次数选取为3.仿真结果表明,在相同误比特率情况下,所提SAGE-IPSO联合估计检测算法的性能优于传统的基于LS信道估计的ML检测算法和基于MMSE信道估计的ML检测算法,其检测性能有了较大改善,在相同误码率的情况下与理想信道估计下的最大似然检测算法仅相差1 dB.

|
图 5 SAGE-IPSO联合估计检测算法的性能 |
针对MIMO-OFDM系统,结合SAGE算法,提出了一种基于改进粒子群优化的联合估计检测算法,给出了具体的实现方案.算法的主要思想是采用DFT-LS对信道进行初估计,利用SAGE迭代过程获得信道状态信息,联合改进粒子群优化算法进行检测,从而在MIMO-OFDM系统信道状态信息不够准确的情况下,获得精确检测.在所设定的仿真参数条件下,对提出的算法进行了仿真分析和性能比较.仿真结果表明,提出的联合估计检测算法优于经典传统检测算法,其性能接近于理想信道估计条件下的ML信号检测算法,在相同误码率的情况下,信噪比损失在1 dB左右.算法具有一定的工程实用价值.
| [1] | Zhang Jian, Huang Xiaojing, Suzuki H, et al. Gaussian approximation based interpolation for channel matrix inversion in MIMO-OFDM systems[J].IEEE Transactions on Wireless Communications, 2013, 12(3): 1407–1417. doi: 10.1109/TWC.2013.011513.121024 |
| [2] | Salvo R P. On throughput of MIMO-OFDM systems with joint iterative channel estimation and multiuser detection under different multiple access schemes[J].IEEE Communications Letters, 2011, 15(8): 831–833. doi: 10.1109/LCOMM.2011.060811.110714 |
| [3] | Piechocki R J, Nix A R, Mcgeehan J P, et al. Joint blind and semi-blind detection and channel estimation[J].IEEE Proceedings Communications, 2003, 150(6): 419–426. doi: 10.1049/ip-com:20030716 |
| [4] | Ylioinas J, Raghavendra M R, Juntti M. Avoiding matrix inversion in DD SAGE channel estimation in MIMO-OFDM with M-QAM[C]//2009 Vehicular Technology Conference Fall(VTC2009-Fall). Anchorage: IEEE Press, 2009: 1-5. |
| [5] | Wang Jyunsheng, Lain J K. Genetical swarm optimization-based symbol detection for MIMO systems[C]//2008 Asia-Pacific Conference on Communications(APCC2008). Tokyo: IEEE Press, 2008: 1-4. |
| [6] | Xu P, Wang J K, Qi F, et al. Space-alternating generalised expectation-maximisation-basedh-infinity channel estimator for multiple-input multiple-output-orthogonal frequency division multiplexing systems[J].Communications, IET, 2011, 5(14): 2068–2074. doi: 10.1049/iet-com.2010.0487 |