2. 北京邮电大学 自动化学院, 北京 100876
通过对目标函数和约束条件进行灵敏度分析, 生成目标函数和约束函数的灵敏度附加项, 提出了2种基于灵敏度附加目标函数的可靠性稳健优化设计模型; 针对不同评价者对目标获取信息的局限性, 基于灰色系统理论把评价者对目标的评估分配在一定范围内, 给出了计算各目标函数权重系数的专家评估方法.应用Matlab7.1语言的优化工具箱和符号工具箱实现圆柱螺旋压缩弹簧的多目标可靠性稳健优化设计.算例表明, 该方法具有较高的精度和可靠度, 为机械零件的可靠性设计提供了理论依据.
2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
Additional items of sensitivity of objective and constraint functions are generated through analyzing the corresponding functions objective functions and constraints. Two models of optimization design for reliability are proposed based on the additional items of sensitivity. According to the limitations of information for objective functions obtained from different evaluators, the objective functions and the evaluators' assessment based on gray system theory was allocated in a certain range. The expert assessment method is presented to calculate the weight coefficients of the objective functions. Reliability-based robust optimization design of cylindrical helix spring is achieved by using the optimization toolbox and symbolic toolbox of Matlab. Numerical examples prove that the proposed approach which provided the theoretic basis for the reliability design of the mechanical elements has a higher precision and reliability.
稳健设计往往是多目标优化问题,传统优化方法[1-4]中目标和约束仅在随机参数均值处取值,未考虑其方差的影响,其方差仍停留在原始设计水平上;罗佑新等[5]提出了一种基于设计变量敏感度的多目标稳健设计方法,同时考虑了设计变量均值和方差的影响,并将可靠度作为目标函数引入多目标优化设计中.但是,以可靠度最高作为目标函数并不尽合理,要求可靠度尽可能大也就是无限趋近于1,当可靠度足够大时,设计尺寸的增加对可靠度数值的影响并不再明显,很难寻得最优解.
笔者在设计阶段以可靠度作为约束条件,同时对目标和约束进行灵敏度分析产生灵敏度附加项,建立了2种可靠性稳健优化设计模型;利用灰色系统理论,给出了计算各目标权重系数的专家评估方法,采用Matlab7.1语言的优化工具箱来实现圆柱螺旋压缩弹簧的多目标可靠性稳健优化设计.
1 多目标可靠性优化设计思想1.1 可靠性随机摄动技术结构可靠性分析的目的就是计算可靠度

|
(1) |
将基本随机参数x=[x1, x2, …, xn]T和功能函数g(x)表示为

|
(2) |

|
(3) |
其中:ε为一小参数,下标d的部分表示基本随机参数中的确定部分,下标p的部分表示随机部分.
对式(2)、式(3) 两端分别取均值和方差,则有
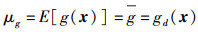
|
(4) |
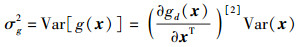
|
(5) |
其中:

根据可靠性指标定义
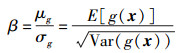
|
(6) |
多目标优化设计的数学模型表达式一般表示为

|
(7) |
其中:x=[x1, x2, …, xn]T和y=[y1, y2, …, yq]T分别为设计变量和预设定的参数向量,f(x, y)是目标函数,g(x, y)是不等式约束,h(x, y)为等式约束.
若要求可靠度指标不小于系统结构给定的可靠度要求R0,则可以求得对应的可靠度指标β0=Φ-1(R0),进而可得可靠度指标约束条件为

|
(8) |
则基于随机摄动技术的多目标可靠性优化设计可以用数学模型表示为
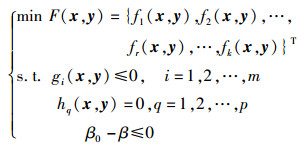
|
(9) |
基于上述模型,加入灵敏度分析产生的目标函数和约束条件的附加项,重新建立目标函数和约束函数,构建基于灵敏度附加项多目标可靠性稳健优化设计模型.
2.1 构建目标函数和约束函数灵敏度附加项令z=[x, y]T=[z1, z2, …, zn]T,那么目标函数对不确定参数的灵敏度为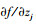
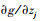
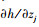
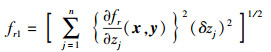
|
(10) |
同时考虑目标函数和约束函数对不确定参数的灵敏度,则目标函数的灵敏度附加项定义为
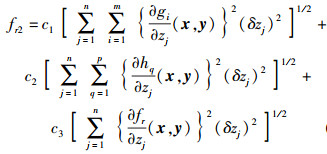
|
(11) |
其中:

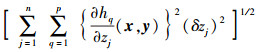
|
为等式函数灵敏度附加项,c1、c2和c3为等式右边3项的权重系数,具体取值参照文献[5].
第i个不等式约束函数基于灵敏度的表达式为
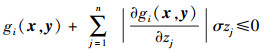
|
(12) |
第q个等式约束函数基于灵敏度的表达式为

|
(13) |
其中:σzj为zj的方差,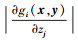
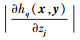
模型Ⅰ
只考虑目标函数对不确定参数变化程度的影响

|
(14) |
模型Ⅱ
同时考虑目标函数和约束条件对不确定参数的灵敏度的影响
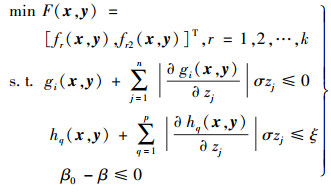
|
(15) |
权重自身所具有的不确定性,当评价等级划分较为细致时,由于获取信息的局限性,评价者往往很难给出一个确定的权重值.因此,把权重分配在一定范围内比较符合实际,区间灰数正适合这种要求.求得各目标函数的权重值就可将多目标问题单目标化,进而利用Matlab语言的优化工具箱和符号工具箱来实现可靠性稳健优化设计.
3.1 基于灰色系统理论的权系数评估法定义F=(f1, f2, …, fr, …, fk)为多目标优化问题的目标函数集,确定任一目标函数fr在系统中的权重时,给fr赋予一个区间灰数⊗λr,那么该区间灰数⊗λr为fr的权.如果λr是区间灰数⊗λr的白化值,则有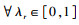
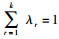
上述定义中用区间灰数表示各个目标函数的权并不是一个确定的数值,而是给出了相应权值的取值范围.假设在一个多目标优化问题中有n个评价者对第r个目标函数fr给出的n个变权为[ar1, br1], [ar2, br2], …, [arn, brn];那么对k个目标函数进行评价就会得到k个区间灰数序列[ar1, br1], [ar2, br2], …, [arn, brn], r=1, 2, …, k.
每个区间灰数序列的综合评价的均值为

|
(16) |
每个区间灰数序列的方差为
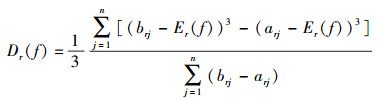
|
(17) |
每个区间灰数序列标准差
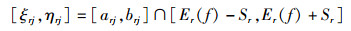
|
(18) |
在整个评价体系中得到一个综合n个评价者意见的各目标函数的权重系数为
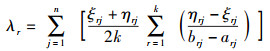
|
(19) |
利用优化工具箱的命令函数fmincon来处理可靠性稳健优化问题, 上述数学模型可表示为

|
fmincon函数的使用格式为

|
其中:xopt是目标函数最优解; fxopt是目标函数在最优点x的函数值; exitflag是算法终止标志; output是返回优化结果; grad是目标函数在最优点x的梯度值; hessian是返回目标函数在最优点x的hessian矩阵; ‘Nlc’是定义非线性约束条件的函数名; p1、p2等是传递函数.
4 应用实例设计某内燃机的气门弹簧,当气门完全开时,弹簧最大变形量δ为(μδ, σδ)=(16.59, 0.15) mm,负载F为(μF, σF)=(680, 34) N,工作频率f为(μfr, σf)=(25, 0.25) Hz, 工作最高温度为(μT, σT)=(150, 1.5)℃,选用50CrVA钢丝.要求簧丝直径2.5 mm≤d≤10 mm,弹簧中径25 mm≤D2≤ 60 mm,有效工作圈数3≤n≤15,旋绕比D2/d≥5,可靠度指标要求大于β0=3.0.
1) 计算各目标的权重
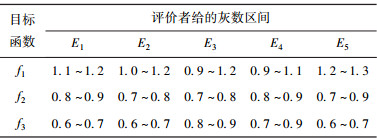
评价者对各个目标的评估灰数如表 1所示.
|
|
表 1 评价者对各目标函数的评估 |
由式(16) 到式(19) 计算,并通过归一化处理后得到各目标函数的权重值为
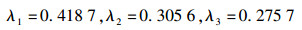
|
2) 可靠性稳健优化设计结果
通过2.2节的模型Ⅰ,结合Matlab优化工具箱中命令函数fmincon,求解结果如表 2所示.
|
|
表 2 优化结果 |
3) 结果分析
① 由设计参数分析,稳健设计结果均略小于普通优化设计,各目标函数值均有所减小;从3种方法得到β1、β2和β3的对比结果可以看出,普通优化设计在各个极限状态下的可靠度指标差距很大,个别不能满足可靠度要求,本方法得到的可靠度在各极限状态下差距不大,且均能满足可靠度要求,从而保证了设计的稳健性.因此,本方法在设计结果的可靠性和稳健性方面明显优于普通优化设计.
② 由模型Ⅰ和模型Ⅱ结果分析,各设计参数结果不同,但是各目标函数值高度一致,证明了2种模型的正确性;通过各极限状态下的可靠度证明了模型Ⅱ比模型Ⅰ更稳健可靠;优化设计问题中若有多个复杂约束,模型Ⅱ计算量要远大于模型Ⅰ,所以在一般优化问题中选择模型Ⅰ有助于计算,且也能保证有足够的可靠度和稳健性,模型Ⅱ更适合高可靠性高精度要求的模型.
5 结束语针对多目标优化问题提出的2种可靠性稳健设计模型, 同时考虑了目标函数和约束条件对不确定参数的灵敏度,具有高可靠度和高稳健性的优点.在圆柱螺旋压缩弹簧的多目标可靠性稳健设计中,与普通优化设计相比较,本方法在一定程度上提高了圆柱螺旋压缩弹簧的设计质量、安全性和鲁棒稳定性.由于同时考虑了设计变量的均值和方差对目标函数、约束函数的影响,所以使得设计结果更符合实际.该设计方法对于其他机械结构的优化设计也有一定的参考和应用价值.
| [1] | Ognjanovi′c M, Miloš R, Predrag Ž. Reliability for design of planetary gear drive units[J].Meccanica, 2014(49): 829–841. |
| [2] |
魏锋涛, 宋俐, 李言. 机械多目标灰色与模糊优化设计方法[J]. 计算机集成制造系统, 2010, 16(9): 1823–1827.
Wei Fengtao, Song Li, Li Yan. Mechanical multi-objective optimal design methods based on grey and fuzzy theory[J].Computer Integrated Manufacturing Systems, 2010, 16(9): 1823–1827. |
| [3] | Garg H, Rani M, Sharma S P, et al. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment[J].Expert Systems with Applications, 2014, 41(7): 3157–3167. doi: 10.1016/j.eswa.2013.11.014 |
| [4] | Giuggioli B P, Marseguerra M, Zio E. Multi-objective optimization by genetic algorithms: application to safety systems[J].Reliability Engineering and System Safety, 2001(72): 59–74. |
| [5] |
罗佑新, 车晓毅, 杨继荣, 等. 高维多目标灰色稳健优化设计及其Matlab实现[J]. 农业机械学报, 2008, 39(8): 157–160.
Luo Youxin, Che Xiaoyi, Yang Jirong, et al. Grey robust optimization design of high dimension multi-objective and its achieving with matlab[J].Transactions of the Chinese Society of Agricultural Machinery, 2008, 39(8): 157–160. |
| [6] | Teixeir A A, Cunha A E, Clemente J J, et al. Modeling and optimization of a recombinant BHK-21 cultivation process using hybrid grey-box systems[J].Journal of Biotechnology, 2005, 118(3): 290–303. doi: 10.1016/j.jbiotec.2005.04.024 |