推荐技术的研究吸引了来自机器学习、数据挖掘、信息检索等不同领域的研究者，但是，大多数推荐系统都受以下问题的困扰：1) 数据稀疏性问题，Badrul等^[1]的研究表明，大多数用户只对极少数物品评分，稀疏的评分数据常使得推荐系统无法准确捕捉用户的偏好；2) 冷启动问题，当新构建的推荐系统没有评分历史数据或者新用户加入时，系统无法学习用户的偏好，因此推荐效果不理想；3) 传统的推荐技术忽略了用户之间的社会关系这一重要因素.笔者的研究目标是将用户的社会关系融入推荐系统，解决或减轻推荐系统所面临的数据稀疏性、冷启动等问题，使推荐过程更加符合现实情况，提高推荐系统的性能.笔者主要基于如下假设：用户的偏好可以通过对评分矩阵的因式分解得到；用户的偏好不是独立的，会受到来自其朋友的影响；用户之间的社会关系越亲近，他们的偏好就越相似.

构建社会化推荐系统的过程可分成紧密相关的两个任务，一个是度量用户的社会相似度，另一个是利用社会关系和评分数据构建社会化推荐系统.度量用户的社会相似度本质上是图上的连接预测问题，即度量图上结点之间的相似性的问题.基于共同邻居的度量方法计算量小，但只考虑到图结构的本地一致性；基于路径的度量方法虽然考虑到图结构的全局一致性，但是往往计算量很大.而流形排序算法同时考虑了图结构的本地一致性和全局一致性，迭代过程简单，适用于各种类型的图.针对社会网络的大规模和稀疏性特点，笔者拟用流形排序算法度量用户的社会相似度.

当前，已有研究者提出若干社会化推荐系统，SocialMF模型^[2]将信任关系融入矩阵分解，但该方法假定用户的偏好完全由其朋友的偏好均值决定. STE模型^[3]认为用户的偏好由自己和所信任的人共同决定，但训练过程比较复杂. Ma等^[4]提出了基于正则化技术的SR1模型和SR2模型，SR1模型假定用户的偏好取决于其直接朋友偏好的加权平均值，SR2模型则强调偏好在用户之间的传播以及由此形成的直接/间接朋友之间偏好的一致性，实验结果表明，SR2模型显著优于SR1模型.

针对SR2模型强调偏好传播的特点，利用基于得分传播机制的流形排序方法度量用户之间的全局相似度的方法，并提出一种结合SR2模型和流形排序方法的新的社会化推荐方法.

推荐系统包含用户集合U={u₁, u₂, …, u_M}以及物品集合O={i₁, i₂, …, i_N}，用户对物品的评分为R=[R_{u, i}]_M×N，R_{u, i}表示用户u对物品i的评分，分值常常是1~5的整数.用户的社会关系由邻接矩阵A=[A_{u, v}]_M×M表示，A_{u, v}表示用户u和用户v之间存在的社会关系，1表示存在，0表示不存在.社会化推荐系统的任务是：如果用户u没有对物品i评分，根据评分矩阵R和社会关系矩阵A来预测用户u对物品i的评分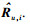

隐语义模型^[5]认为每个用户的偏好仅由少量的因素决定，物品的特征也是由少数因素决定的.假设M, N分别表示用户和物品数量，D为特征的个数，且D < min(M, N)，以矩阵U_M×D表示用户的偏好，每个用户的偏好用向量U_i表示，即U中的一行；同理，以矩阵V_N×D表示物品的特征，每个物品的特征表示为V_j；用R_M×N表示评分矩阵. Thomas^[5]认为评分R_{u, i}由用户u的偏好和物品i的特征共同决定，可以利用低阶矩阵分解方法进行评分预测，R≈U^TV.该低阶矩阵分解问题可转化为一个最优化问题，，这里‖·‖_F表示矩阵的Frobenius范数，为评分的预测误差的平方和，通过求解该函数的最小值，可以得到U和V.由于R中大多数元素缺失，所以可进一步将该函数的优化问题重写为

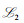
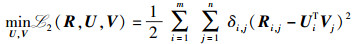
(1)

其中：δ为指示函数，如果R_{i, j}有值，则δ_{i, j}为1，如果R_{i, j}缺失，则δ_{i, j}为0，式(1) 中为避免过度拟合的问题，进一步在目标函数加入变量U，V的正则项

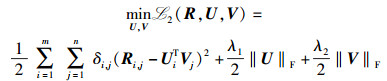
(2)

其中λ₁、λ₂为正则化系数.利用梯度下降算法可以求解上述最优化问题，获得目标函数的局部最小值以及对应的U和V. Ruslan等^[6]利用图模型给出了低阶矩阵分解的概率解释.

协同过滤方法常使用基于评分的相似度，如VSS、PCC、Cosine等，为了将用户的社会关系融入推荐系统，笔者使用用户的社会相似度，提出基于流形排序的社会相似度度量方法.流形排序的过程可以形象地描述为:首先根据社会关系构造一个权重图，并且为目标用户赋以一个初始的正得分, 其余用户的初始得分设为0；然后，所有的节点迭代地将其得分传播给与其相邻的节点，当网络达到全局平衡状态时, 传播过程停止；网络平衡后各个用户得分可被用来度量他们与目标用户的社会相似度.

将用户的社会关系用邻接矩阵A=A_{u, v}]_M×M表示；用户的社会相似度用矩阵S=[S_{u, v}]_M×M表示，所有元素的初始值为零，S矩阵的第u列记为向量S_u，I_M×M为单位矩阵，I中的第u列记为向量I_u.将基于流形排序的社会相似度度量算法描述如下.

算法1基于流形排序的社会相似度度量算法

输入：A_M×M，α

输出：S_M×M

//变量初始化S

S←0_M×M

//用迭代方式计算社会相似度S

W←diag(sum(A))

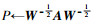
for t from 1 to maxIter₁

  for u from 1 to M

    S_u(t+1)←αPS_u(t)+(1-α)I_u

  end

end

算法首先对A进行对称规范化，这里W为一个对角矩阵，W_{u, u}为各个结点的度，对应于A矩阵第u行元素的和.然后对S_u(t+1)=αPS_u(t)+(1-α)I_u进行迭代，直到收敛.若用S_u^*表示序列{S_u(t)}的极限，则用户u与其他用户之间的社会相似度用S_u^*来表示. Zhou等^[7]证明该流形排序的结果最终会收敛到S_u^*=(1-α)(I-αP)^－1I_u.由于收敛结果包含求逆运算，大数据集会产生很大计算开销，所以本算法选择迭代方式求解.参数α在[0, 1) 之间取值, 参数maxIter₁用于调节流形排序的迭代次数.

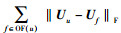
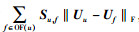
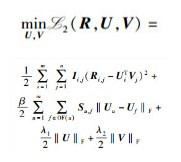
社会网络中，用户与朋友们的偏好是趋于一致的，将用户u和用户f的偏好分别用U_u和U_f表示，则用户u和用户f的偏好的差异可表示为‖U_u－U_f‖_F，用户u与朋友们总的偏好差异可以表示为，式中OF(u)表示用户u认识的朋友，根据上文假设，社会关系越亲近的朋友，对用户u产生的影响越大，用S代表社会相似度，可以得到用户u的加权的偏好差异为，将所有用户与朋友间的偏好差异作为惩罚项加入到式(2)，得到新的融入社会化关系的矩阵分解目标函数，如式(3) 所示.

(3)

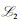
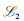
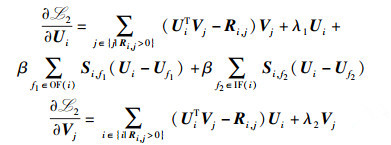
其中：β是正则化系数，与式(2) 类似，式(3) 可以通过梯度下降搜索目标函数的局部最小值，进而求解U、V.为此，这里推导对U、V的偏导数如式(4) 所示.

(4)

根据以上分析，笔者提出基于流形排序和社会化矩阵分解的推荐方法(SMF-MR，social matrix factorization with manifold ranking)，先利用流形排序度量用户的社会相似度，然后将社会关系融入评分矩阵的因式分解.算法2给出SMF-MR推荐算法的算法描述.

算法2 SMF-MR推荐算法

输入：R_M×N，A_M×M，β

输出：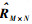

//变量初始化

U_M×D←normal(0, 1)，V_N×D←normal(0，1)

由算法1计算社会相似度S

//用梯度下降算法求解U，V

for epoch from 1 to maxIter₂

  foreach (i, j) in {(i, j)|R_{i, j} > 0}

    根据式(4) 计算

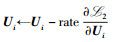
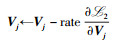
  end

end

//计算预测评分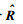

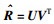
算法的输入包括评分数据R_M×N、社会关系数据A_M×M，输出为预测评分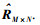除了已经提到的参数λ₁、λ₂、D、β，为了控制算法训练过程，算法还额外引入一些参数：包括学习率rate，社会化分解的迭代次数maxIter₂.用户和物品的特征向量用D维标准正态分布的随机样本进行初始化.

为了验证SMF-MR算法的有效性，实验将基于Flixster和Douban两个真实的数据集. Flixster是一个电影社交网站，Flixster数据集包含大约100万个用户、820万个评分、4.9万部电影、2 670万个双向的朋友关系，评分为取值之间的离散数值，共分10级. Daban是中国最大的在线社会网络之一，Douban数据集包含大学12.9万用户、5.9万部电影、168.3万个评分、169.2万个双向朋友关系，其中评分为1~5之间的数值.

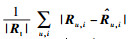
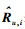
采用了2个度量方法进行评估，评分预测的平均绝对误差(MAE, mean alosolute error)和评分预测的均方根误差(RMSE, root mean square error).实验将评分数据R按比率分成R_l和R_t 2个集合，集合R_l用于学习，集合R_t用于测试，MAE可以定义为.其中：R_{u, i}表示用户u对物品i的真实评分，表示推荐系统对给定的用户u及物品i的预测评分. |R_t|表示用户测试后的评分的个数. RMSE定义为.

可以看出，MAE和RMSE越低预测的精度越高，推荐系统的性能越好.

为了评估笔者提出推荐方法的性能，通过实验与另外3种推荐方法进行了比较：1) 协同过滤方法，使用最广泛的基于内存的推荐方法；2) 概率矩阵分解方法^[6]，采用基本的矩阵分解方法，未将用户的社会关系考虑在内；3) 社会正则化方法(SR2)^[4], 将社会关系融入到矩阵分解，该方法的用户相似度采用了基于评分的VSS相似度和PCC本地相似度，而SMF-MR模型采用了基于流形排序的全局相似度.

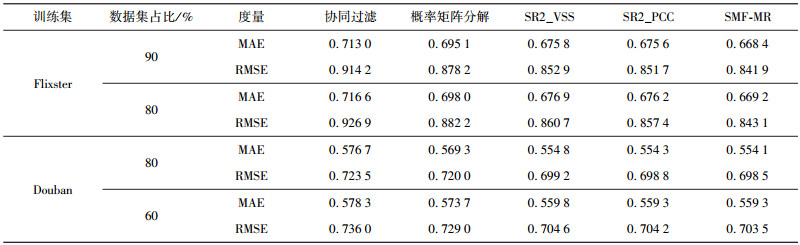
笔者设计了2个实验，实验1分为2组，分别度量各种推荐方法的MAE值和RMSE值.第1组实验在Flixster数据集上进行，由于Flixster数据集比较稀疏，实验随机选取90%和80%的评分数据作为训练集，余下部分作为测试集.第2组实验在Douban数据集上进行，实验随机选取80%和60%的评分数据作为训练集，余下的为测试集.为了得到稳定的度量结果，实验将每组实验重复5次，度量的结果取各次度量结果的平均值.实验中，正则化参数λ₁、λ₂、β的取值均为10^-3，维度D取值为经验值10，由于协同过滤不是基于矩阵分解的方法，所以不考虑这几个参数；流形排序参数α取经验值0.99.各种推荐方法的性能比较如表 1所示.

表 1

表 1

表 1 各种推荐方法的推荐性能比较(维度D=10)

表 1 各种推荐方法的推荐性能比较(维度D=10)

从表 1的结果可以看出，笔者提出的推荐方法所得到的MAE和RMSE结果稳定地低于其他方法.而Douban数据集上的实验结果低于Flixster数据集上的实验结果，这说明Flixster数据集可能包含较多的噪声.

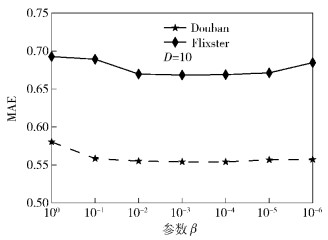
上述实验中，SMF-MR中的参数λ₁、λ₂、D、α采用了普遍接受的经验值^[6]，而参数β控制着社会关系在系统中的重要性，β越大则社会关系对系统的影响越大，因此，实验2着重研究了参数β对SMF-MR性能的影响，通过调整β的不同取值，观察β对SMF-MR模型性能的影响，结果如图 1和图 2所示. 图 1显示了参数β在不同的取值情况下，SMF-MR在两个数据集上的评分预测的RMSE误差的变化情况，从图 1可以看出，β值小于10^-4或者大于10^－2时都会引起RMSE的值上升(系统性能下降). 图 2显示了参数β对评分预测的MAE的影响，β值小于10^-4或者大于10^-3时都会引起MAE值上升，因此，实验1中β的值设为10^-3是合理的.上述实验结果同时也说明，适当地考虑社会关系对推荐过程的影响, 可以进一步提高传统推荐系统的性能.

图 1

图 1

图 1 参数β对RMSE的影响

图 2

图 2

图 2 参数β对MAE的影响

提出一种基于流形排序和矩阵分解的社会化推荐方法(SMF-MR)，该方法将用户之间的社会相似性融入到评分矩阵的低阶矩阵分解过程，采用流形排序方法度量用户的社会相似度，通过学习得到表

示用户偏好和物品特征的低阶隐含语义矩阵，进而利用低阶隐含语义矩阵进行评分预测.实验表明，该方法在大型数据集上比同类的方法具有更好的性能.主要贡献在于3个方面：1) 将流形排序方法用于度量用户社会关系的亲近程度，并将度量结果用户社会化推荐系统；2) 指出了SR2模型在用户相似度度量上存在的不足，在结合SR2模型和流形排序的基础上，提出了融入全局社会相似度的SMF-MR推荐方法，实验表明，不论与同类的推荐方法还是SR2模型相比，SMF-MR方法均提高了推荐系统的精度；3) 提出的SMF-MR社会化推荐方法通过同时使用社会网络和传统评分两种数据，可减轻数据稀疏性问题、冷启动问题对推荐系统的影响.