2. 安徽省现代成像与显示技术重点实验室, 合肥 230039
为了改善传统的多幅亚像素图像配准融合实现超分辨率的方法面临的配准误差和高成本问题, 将压缩传感理论引入超分辨率成像.基于大多数自然图像普遍具有的稀疏表示特性, 以经典的4-f光学架构为基础, 利用频域中相位比振幅包含更多信息的特点, 提出了一种频域纯相位调制压缩成像方法, 通过重建算法从单次曝光记录的低维测量值中恢复原高分辨率图像的信息.数值实验结果表明, 提出的方法可以有效地实现图像信息的随机调制和高质量重建, 是一种有潜力的压缩成像物理实现方案, 具有较高的重建信噪比和较少的重建时间, 尤其是对于大尺度图像.
2. Key Laboratory of Modern Imaging and Displaying Technology of Anhui Province, Hefei 230039, China
One of the goals of optical imaging and image processing is super-resolution imaging. In order to reduce the registration error and costly problem facing in multiple sub-pixel image registration fusion method to achieve super-resolution, a compressive sensing method is introduced for super-resolution imaging, it benefits from the general sparse representation feature of most nature images. Based on the classical 4-f optical architecture, the phase will contain more information than the amplitude in frequency domain, a compressed imaging method with pure phase modulation in the frequency domain is proposed. The original high-resolution image information can be recovered from the low-dimensional measurements recorded with a single exposure by various algorithms. Numerical results demonstrate that the proposed can effectively achieve random modulation of image information and high-quality reconstruction, which can be considered as a promising scheme for physics implementation of compressed imaging with high reconstruction signal to noise ratio and less reconstruction time, especially for large-scale image.
压缩成像(CI,compressed imaging)是压缩传感理论最核心的应用领域之一,相比经典的成像模式,CI方法利用图像所具有的稀疏特性,具有重要的潜在优势,可以克服经典成像系统的不足[1-3].
针对Stern等[2-3]提出的CI方法迄今为止仅限于压缩成像理论研究,未进一步考虑CI系统的实现问题,笔者提出一种频域相位随机调制的压缩成像方法,然后采用两种非线性CS重建算法从低分辨率测量数据中恢复原对象的信息.该方法可在单次曝光条件下有效地实现大尺度图像信息的随机调制与高质量重建,具有较高的重建信噪比和较少的重建时间,在视频等动态场景领域具有重要应用前景.
1 压缩感知基本原理2006年,Donoho[4]和Candès[5]等率先提出压缩传感理论.其核心思想是:对于一个稀疏或可压缩信号,可以利用远少于Nyquist采样定理所要求的线性非相干测量实现信号的压缩采样,然后从欠采样数据中重建原信号.
压缩成像的欠采样模型为
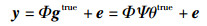
|
(1) |
其中:Φ为线性测量算符,通常由成像系统和衍射定理确定;Ψ表示稀疏算符,如DCT,各种类型的小波基等;gtrue为由二维图像按照一定顺序排列成的列向量;θtrue为gtrue在稀疏算符Ψ上的表示系数,是K稀疏的;y∈RM和e∈RM分别表示测量向量和噪声向量.
如果测量算符Φ满足2K阶的限制等距性质(RIP, restricted isometry property),那么可以通过求解下面的
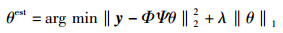
|
(2) |
其中:第1项是保真项,用于保证解θest满足观测值的约束;第2项是用于表征稀疏度的正则化项,λ是正则化参数.
2 频域随机相位调制压缩成像模型众所周知,在频域中,相位包含绝大部分信息.利用这一点可以更有效地实现信号的调制,以经典的4-f光学架构为基础,通过在频域实现相位的随机延时来实现信息的随机调制.该方法可以统一在卷积模型的框架之下,有效地处理大尺度图像的压缩采样问题,具有重要优势.
2.1 频域随机相位调制原理从基于卷积原理的基本成像模型出发,其数学模型为

|
(3) |
其中:g∈Rn×n表示待重建的原图像,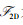
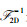
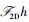
基于4-f光学架构实现频域随机相位调制压缩成像的主要思路是利用频域随机相位实现图像信息的随机调制,然后通过低分辨率CMOS器件记录测量值.该方法可以通过单次曝光一次性捕获所有测量值,不再需要采集任何额外的信息.
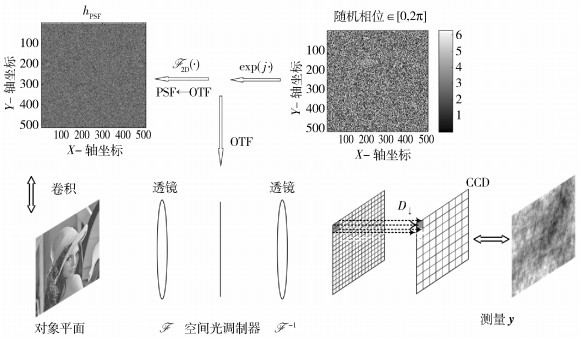
注意,笔者考虑的是单色相干光源照明成像设置,该过程的具体方案如图 1所示.
|
图 1 4-f傅里叶光学成像架构实现随机卷积 |
在图 1中,频域随机相位调制(RPM, random phase modulation)是通过光电器件——空间光调制器(SLM, spatial liquid modulator)来实现不同点的不同相位延时.该SLM是纯相位调制器件,复振幅经过SLM调制后保持不变,而每一点的频域复振幅经过不同的相位延时,从而完成频域相位的随机调制.前一个透镜完成的是傅里叶变换,将光场变换到频域,后一个实现傅里叶逆变换,将光场再次转换到空间域.
最终基于频域随机相位调制的CI模型为
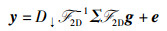
|
(4) |
其中:D↓表示下采样操作,如积分下采样、随机位置下采样等.
Romberg等[7]的研究表明,如果误差e的大小可以是有界的,即‖e‖2≤ε,给出式(2) 的一个松弛版本的解θ*,将服从
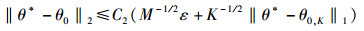
|
(5) |
其中:C2是某个正常数,M是测量数目,K是稀疏度.
3 模拟实验下面给出4组数值模拟实验验证笔者提出的CI方法的有效性.第1组数值实验结果在图 2中给出,用于说明该方法的应用潜力.实验设置为:32位Windows7操作系统,四核Intel(R) Core(TM) i5-2320处理器,主频3 GHz,有效内存3.0 G,测试软件是Matlab2010a.第1组数值实验中,测试图像选用Lena和Phantom图像,2幅图像的像素数目皆为1 536×1 536,采用图 1中给出的光学成像结构得到低分辨率的测量值,然后通过重建算法从测量值中恢复原高分辨率的图像,实验结果如图 2所示.

|
图 2 随机相位调制超分辨成像实验 |
图 2中的实验分别是Lena和Phantom图像的实验结果,其中图 2(a)是原始的Lena图像,图 2(b)是Lena图像经过图 1中的CI系统得到的低分辨率测量值,水平方向与垂直方向的下采样因子皆为4,测量值y的像素数为384×384.总降采样率M/N为1/16. 图 2(d)和图 2(e)是图 2(b)中所示的测量值y分别通过迭代软阈值(IST, iterative soft thresholding)[8]和梯度投影稀疏重构(GPSR, gradient projection for sparse reconstruction)[9]算法得到的Lena图像重构的估计结果,其信噪比分别是29.61 dB和29.84 dB. 图 2(e)~图 2(h)则分别对应Phantom图像的原图,经过图 1中的CI系统得到的低分辨率测量值y(降采样因子和Lena图像相同,像素数目为384×384),以及分别采用IST算法和GPSR算法重建出的估计结果,二者的信噪比分别是39.74 dB和39.87 dB. 图 2实验中使用的稀疏算符Ψ是Rice大学提供的尺度为3的Daubechies 10小波基(RWT, rice wavelet toolbox),下面的各组实验也都基于同样的小波稀疏算符与参数选择,重构算法也都采用IST和GPSR算法.
在实际成像系统中必须考虑诸多噪声干扰,因此设计第2组数值实验测试不同标准差的高斯随机噪声条件干扰下的重建图像的误差曲线.测试图像仍然选用图像Lena、Cameraman和Phantom,像素数为1 536×1 536,下采样率Ds分别选用2、3、4、6,噪声标准差σ=[0, 0.4, 0.8, 1.2, 1.6, 2.0],采用信噪比(SNR, signal to noise ratio)度量重建图像的好坏,比较结果如图 3所示.

|
图 3 不同噪声的随机相位编码图像重建性能比较 |
从图 3中可以看出,在相同噪声标准差和相同下采样率Ds的条件下,Phantom图像的SNR值最高,Cameraman次之,Lena最差.其原因是在相同参数设置下,Phantom图像的稀疏度K值最小,而Lena图像的稀疏度K值最大.由此导致在同样的测量数目条件下重建图像SNR大小的差异.
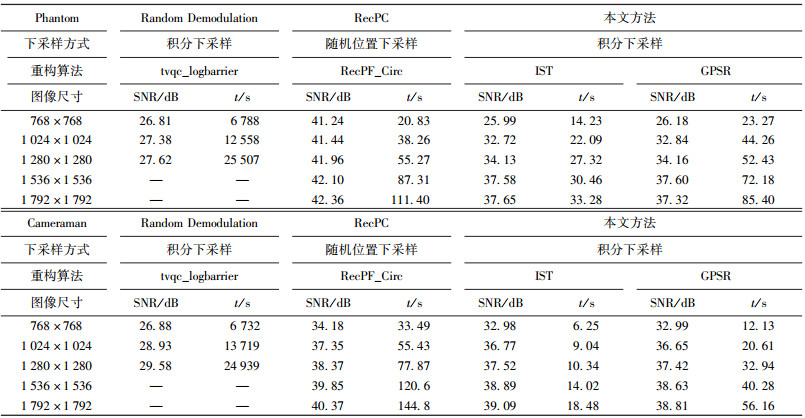
为验证提出的CI方法的优势,设计第3组比较实验,对比方法选用Romberg在文献[7]中提出的随机解调(RD, random demodulation)方法和Yin等人提出的RecPC[10]方法. Cameraman和Phantom测试图像的像素数分为768×768,1 024×1 024,1 280× 1 280,1 536×1 536和1 792×1 792.
积分下采样率M/N为1/8,其原因是RD方法中使用随机解调测量与低分辨率测量组成的混合测量;二者各占总像素数的1/16,导致总的下采样率是1/8.另外,RecPC方法的下采样方式是随机位置下采样,就是从N个位置均匀随机地抽取M(M=N/8) 个位置对应的测量值.而笔者采用积分下采样方式,水平方向下采样因子为1/2,垂直方向下采样因子为1/4,这样的参数选择是为了更好地和RD方法保持一致.测试指标包括在给定的参数条件下的3种CI方法的最大的可放大倍数,重建信噪比与重建时间,具体测试数据如表 1所示.
|
|
表 1 3种压缩成像方法重建性能测试 |
由表 1可知,RD方法求解器是tvqc_logbarrier,可以求解的图像尺寸是1 280×1 280这一级别(“-”符号意味着实验程序无法执行),此方法仅在Phantom图像(Cameraman图像则不是)在768×768这个级别上的重建SNR高于笔者的方法,其余则是笔者的方法占据显著的优势.此外,RD方法的重构时间随着放大倍数的增加而迅速增加,笔者的方法在同样参数的情形下,通常仅需要约1%的重建时间,甚至更少.另一方面,与RecPC方法相比,虽然笔者提出的方法得到的SNR值较低(尤其是Phantom图像,是梯度稀疏的),但是RecPC方法的下采样方式是随机位置下采样,数据获取效率非常低,实用性较差.
4 结束语给出一种以经典的4-f光学为基础,通过频域纯相位随机调制实现的压缩成像超分辨率的方法.数值实验结果表明,该方法可以通过单次曝光记录所有的测量值,然后成功重建出原高分辨率的图像.该方法易于物理实现,对压缩成像的实用研究,特别是大尺度图像,具有非常重要的意义.该方法可以很容易地推广到视频压缩成像,是下一步的研究方向之一.
| [1] | Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling[J].IEEE Transactions on Signal Processing Magazine, 2008, 25(2): 83–91. doi: 10.1109/MSP.2007.914730 |
| [2] | Stern A, Javidi B. Random projections imaging with extended space-bandwidth product[J].Journal of Display Technology, 2007, 3(3): 315–320. doi: 10.1109/JDT.2007.900919 |
| [3] |
张成, 杨海蓉, 韦穗. 循环-托普利兹块相位掩模可压缩双透镜成像[J]. 光学学报, 2011, 31(8): 106–111.
Zhang Cheng, Yang Hairong, Wei Sui. Compressive double-lens imaging using circulant-toeplitz-block phase mask[J].Acta Optica Sinica, 2011, 31(8): 106–111. |
| [4] | Donoho D. Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 |
| [5] | Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083 |
| [6] | Tropp J A, Laska J N, Duarte M F, et al. Beyond nyquist: efficient sampling of sparse bandlimited signals[J].IEEE Transactions on Information Theory, 2010, 56(1): 520–544. doi: 10.1109/TIT.2009.2034811 |
| [7] | Romberg J. Compressive sensing by random convolution[J].SIAM Journal on Imaging Sciences, 2009, 2(4): 1098–1128. doi: 10.1137/08072975X |
| [8] | Bioucas D J M, Figueiredo M. A new TwIST: two-step iterative shrinkage/thresholding algorithms for image restoration[J].IEEE Transactions on Image Processing, 2007, 16(12): 2992–3004. doi: 10.1109/TIP.2007.909319 |
| [9] | Figueiredo M, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586–597. doi: 10.1109/JSTSP.2007.910281 |
| [10] | Yin Wotao, Morgan S, Yang Junfeng, et al. Practical compressive sensing with toeplitz and circulant matrices. Visual Communications and Image Processing 2010. International Society for Optics and Photonics, 2010. http://spie.org/Publications/Proceedings/Paper/10. 1117/12. 863527. |