针对正交频分多路复用(OFDM)系统,比较了基于压缩感知的不同导频设计方案及相应信道估计性能.基于信道响应的时域稀疏和缓变特征,提出了基于联合稀疏模型的压缩感知信道估计方法,进一步提高了信道估计的性能.该方法将连续若干个OFDM符号的信道估计问题转化为联合稀疏模型下的压缩感知问题,充分利用信道的稀疏特性和时间相关性进行信道估计.结合短波OFDM系统,比较了几种信道估计方法的性能.仿真结果表明,与传统的最小平方误差信道估计方法和逐符号的压缩感知信道估计方法相比,基于联合稀疏特征的信道估计方法可进一步改善估计性能,对时变信道具有更好的适应性.
Pilot design schemes and their corresponding channel estimation methods for orthogonal frequency division multiplexing(OFDM)system based on compressed sensing theory are studied. With the channel sparse impulse response and slow varying character, a joint sparse model (JSM) for the channel estimation in OFDM system is proposed. With such joint sparse model, the channel estimations of continuous OFDM symbol periods are converted into a sparse vectors recovery problem with joint sparse model, which improves the estimation performance. Different channel estimation methods for shortwave OFDM system are compared. Simulation shows that the proposed compressed sensing based channel estimation scheme brings out better performance compared with conventional least square channel estimation method and symbol-by-symbol compressed sensing channel estimation method. Simulation also shows that the proposed method has better estimation performance under time-variant channel.
OFDM系统中,信道估计的准确程度对系统性能的影响很大.为提高信道估计的性能,广泛采用导频辅助的信道估计方法[1].传统导频辅助法通过估计OFDM导频位置的信道信息,再以插值方式获得其他子载波处的信道信息.经典算法包括最小二乘(LS,least square)信道估计算法[2]和基于最小均方误差(MMSE,minimum mean square error)的信道估计算法[3]. LS算法结构简单,计算复杂度低[4],是目前大多数OFDM系统采用的方法之一.
与传统OFDM信道估计方法不同,基于压缩感知(CS,compressed sensing)的信道估计通过导频估计信道多径参数,再重构信道的频域特性来估计其他子载波处的信道信息.实际中,多径信道通常具有时域上的稀疏特征,需要估计的多径参数减小,可通过更少的导频数估计出整个信道的频响特性,从而减小导频开销,提高频谱利用率.因此,基于压缩感知的无线信道估计技术近年来受到重视[5-6]. Taubock等[5]基于多径信道的时域稀疏特征,研究了基于压缩感知的信道估计模型和方法. Bajwa等[6]研究了频率选择性信道和非频率选择性信道下的压缩感知信道估计问题. Qi Chenhao等[7-10]研究了OFDM系统信道估计中导频的选取问题.基于联合稀疏模型的分布式压缩感知[11]理论,王韦刚等[12]考虑了多传输节点的情况和多信道共稀疏性的问题,提出了一种改进的联合重构算法.
实际应用中,无线信道呈现时变多径特征,相对于信息传输而言,通常情况下信道变化缓慢.对OFDM系统而言,信道在多符号间呈现较强的相关性.如何利用信道的缓变特征和信道时域稀疏特征,设计合适的OFDM信道估计方式,从而减小导频开销是主要研究内容.基于信道的时域稀疏特性和相关性,笔者将联合稀疏模型引入基于压缩感知的OFDM信道估计,提出一种联合稀疏模型的信道估计方法,并比较了OFDM系统不同导频设计方式的性能.仿真结果表明,与传统的信道估计方法相比,基于压缩感知的信道估计方法可大大减少导频的开销,本研究的实验系统中,基于压缩感知的导频开销是传统基于LS信道估计导频开销的1/8.此外还比较了信道时变场景下不同导频设计的性能.
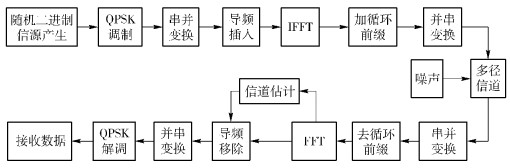
1 OFDM压缩感知信道估计模型N个子载波的OFDM等效基带系统如图 1所示,其中Np个子载波为导频,IFFT(inverse fast Fourier transformation)是反快速傅里叶变换,FFT(fast Fourier transformation)是快速傅里叶变换.
|
图 1 OFDM等效基带系统框图 |
发送信号经过OFDM调制(N点IFFT),接收端OFDM解调后收到的信号可表示为
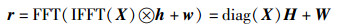
|
(1) |
其中:r、X、w、H、W均是N×1的列向量,r表示接收到的频域信号,X为发送的复信号,w、W分别为信道引入的时域和频域的加性高斯白噪声,h为信道的离散时域冲激响应,H为信道对应的频域响应.对应导频位置P={p1, p2, …, pNp}的接收信号为
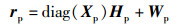
|
(2) |
其中:Xp、rp、Hp、Wp分别是发送信号、接收信号、信道频域响应、噪声在导频位置处的值.
设时变信道冲激响应为

|
(3) |
其中:hk(t)、τk(t)为第k径的复增益和时延,其变化快慢取决于信道的多普勒参数,K为多径径数.实际应用中,OFDM系统的循环前缀(CPcyclic prefix)长度通常设计为大于信道的总时延,因此,假设在一个OFDM符号中,信道参数不变,对具有N个子载波的OFDM系统,对应的离散信道冲激响应为
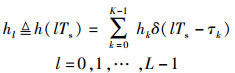
|
(4) |
当系统抽样间隔Ts足够小时,信道时延可近似认为是信道间隔的整数倍.假设时延τk为系统采样间隔的整数倍,且(L-1)Ts=τK-1.可以看到,离散信道冲激相应hl只有当lTs=τk时不为0,因此离散信道冲激响应向量h=(h0, h1,…, hL-1)T-是一个只有K个位置不为0的稀疏矢量,其对应的频域响应为
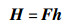
|
其中F是N×L的FFT矩阵,对应导频位置处的频率响应为
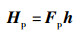
|
(5) |
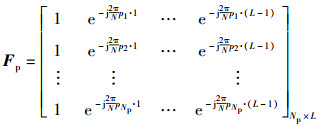
|
综合式(2) 和式(5),得到
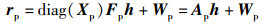
|
(6) |
当导频数小于L时,上述问题变成一个欠定方程的求解问题.由于式(6) 中h是稀疏矢量,根据压缩感知理论,该欠定方程的求解可以通过求解如下优化问题获得信道参数h的估计:
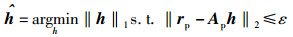
|
(7) |
其中Ap=diag(Xp)Fp.
近年来, 压缩感知理论的发展为上述问题的求解提供了相应的算法,其中主要包括基于贪婪搜索的算法、松弛凸优化等算法,这里不再赘述.
基于信道的时域稀疏特征,即h的稀疏性,利用压缩感知理论,在不影响信道恢复质量前提下可以有效减小OFDM系统导频的个数,从而提高OFDM系统子载波的利用率.目前,基于压缩感知的OFDM信道估计大多数采用逐符号方式,即在每个OFDM符号中放置若干导频,通过导频逐符号估计整个带宽内的频域响应.这种逐符号信道估计方式简单实用,但未充分利用信道的时变特征.通常情况下,由于信道变化率相对OFDM符号速率而言较慢,所以各OFDM符号间的信道特征呈高度的相关性,各符号对应的信道在时间上具有共稀疏的特征.针对信道的共稀疏特征,提出了基于联合稀疏模型的OFDM导频设计和信道估计方法,并比较了不同信道变化率、不同导频设计方案的性能.
2 基于联合稀疏模型的信道估计对于连续M个OFDM符号时间内的信道估计,得到
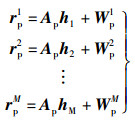
|
(8) |
其中:rpi、Wpi、hi表示连续第i个OFDM符号对应的导频处的接收信号、频域噪声以及相应的信道冲激响应,1≤i≤M.当信道缓变时,待估计的连续OFDM符号对应的信道响应hi具有较强的时间相关性.基于此,采用联合稀疏模型[14]对多符号信道冲激响应进行建模,并获得相应的信道估计算法.
式(8) 中各OFDM符号的导频矩阵Ap是相同的,即导频位置相同.笔者所提出的改进方式是对连续多个OFDM符号中采用不同导频插入方式接收到的导频信号,如式(9) 所示
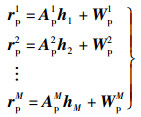
|
(9) |
其中: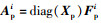
针对式(8)、式(9) 的联合稀疏模型,构造如下的优化问题用于联合信道估计:
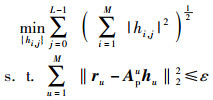
|
(10) |
其中:hi, j表示hi中第j个元素,ε为与噪声有关的一个参量.上述优化问题可由联合正交基匹配算法获得[13].
输入:单次观测向量ri,观测矩阵Φi,最大迭代次数N.
初始化:初始残差向量vi, 0←ri,稀疏位置集C←∅,迭代次数k←0.
重复:
k←k+1;
选取:

|
更新:

|
直到:k≥N
输出:重构信号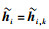
针对提出的联合稀疏模型下的OFDM导频设计和信道估计方法,进行了相应的仿真实验.仿真设定OFDM系统子载波数为256,循环前缀长度为64个采样点,不特别说明情况下导频数为16,导频采用全1导频.导频位置随机生成,LS导频采用最优的等间隔导频.信号调制方式采用QPSK调制, 无信道编码.多径信道采用4径等功率瑞利衰落信道,信道最大时延扩展不超过CP长度,不同信噪比(SNR,signal to noise ratio)下进行5 000次重复实验. LS信道估计中首先对导频位置进行信道估计,对于非导频位置信道响应通过内插运算得到,仿真中假定系统完全同步.单个OFDM符号的信道估计采用正交匹配追踪(OMP, orthogonal matching pursuit)算法进行估计,基于联合稀疏模型的多个OFDM符号的信道估计采用联合正交匹配追踪(SOMP, simultaneous orthogonal matching pursuit)算法进行估计.仿真中,取4个连续OFDM符号进行联合信道估计.
首先,比较了传统LS信道估计与逐符号压缩感知信道估计的性能;其次,针对不同信道变化率,比较了联合稀疏信道估计方法与块状导频的CS估计的性能,这里块状导频方案是利用信道缓变特征,间歇式地在一个OFDM符号中放置导频,估计出的信道参数供后续的连续若干OFDM符号使用.
仿真比较了不同导频方案下信道估计的均方误差(MSE, mean square error)以及信号的误比特率.定义SNR为OFDM调制后的信号功率与噪声功率的比值,信道估计MSE定义为
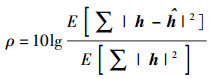
|
(11) |
其中:h为理想信道冲激响应,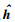
图 2所示为基于压缩感知的信道估计与基于LS的信道估计的性能比较.可以看到,相同信道下,信道估计误差相当的情况时,基于压缩感知的信道估计需要的导频数为基于LS信道估计所需导频数的1/8,基于压缩感知的信道估计可以大大节约用于信道估计的导频数.

|
图 2 CS信道估计与LS信道估计的导频数比较 |
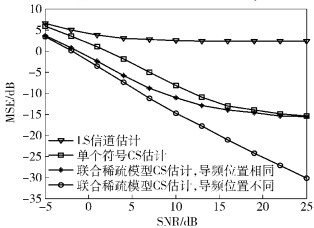
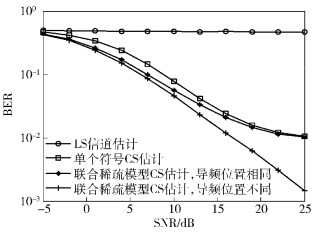
图 3所示为不同导频方案下的信道估计性能比较,图 4所示为相应信道估计下的系统误比特率.从图 3、图 4对比可知,基于压缩感知的OFDM信道估计性能和误码性能比传统的LS信道估计好.这是因为基于CS的OFDM信道估计充分利用了信道的稀疏特性,而且CS估计可以在导频数很少的情况下较好估计信道,传统的LS却不能.从图 2也可以看出这一点,由于导频数目较少,即使在很高的信噪比下,LS信道估计的结果仍然存在较大的误差.从复杂度看,传统LS信道估计需要矩阵逆运算量,其复杂度约为O(Np3), 而基于CS的信道估计方法中,采用贪婪OMP类的算法,其主要的运算量是迭代算法中的求逆运算.但通常情况下,其求逆运算的矩阵大小与稀疏度K相当,在大多数实际应用中,导频数大于K.因此,基于CS的信道估计复杂度与传统LS信道估计的复杂度相当,甚至在导频数远大于稀疏度时,CS的信道估计复杂度低于传统LS信道估计复杂度.
|
图 3 不同信道估计的MSE曲线 |
|
图 4 不同信道估计方法的BER曲线 |
此外,由图 3、图 4可见,笔者提出的联合稀疏模型的CS估计方法比逐OFDM符号的CS估计性能好,这是因为在联合稀疏模型中利用多个OFDM符号共同进行估计,有效利用了信道时间相关性,对信道稀疏位置的确定更准确、可靠.当信噪比较高时,连续OFDM符号导频位置相同的联合稀疏模型CS估计性能趋于单个符号的CS估计结果,而导频位置不同的联合稀疏模型CS估计仍然有性能上的提升,原因在于信噪比较高时,噪声影响小,CS估计性能受限于观测矩阵,导频位置不同的联合CS估计相当于对信道进行了多次不同的观测再联合估计,所以性能优于导频位置相同的情况.
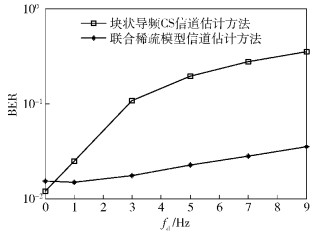
图 5、图 6的仿真结果反映了信噪比SNR为15 dB时,块状导频信道估计方法与联合稀疏信道估计方法的MSE和误码率BER随信道变化率的性能.为确保性能比较的公平性,仿真中对于块状导频信道估计方法,在第1个OFDM符号内采用64个导频,并用压缩感知方法进行恢复,而之后的3个OFDM符号不传输导频,其信道估计结果沿用第1个OFDM符号的信道估计结果.联合稀疏信道估计方法则采用联合稀疏模型进行压缩感知信道估计,每个OFDM符号中有16个导频用于信道估计,各个符号的导频位置不同(所使用的导频数总和仍然是64个).信道仍采用4径等功率瑞利衰落信道,信道变化率由多普勒频偏fd决定.仿真中设定采样率为16 kHz, 信道最大多径时延扩展为4 ms, 一个OFDM符号持续时间为20 ms, 其他的仿真参数默认与之前一致.

|
图 5 fd对信道估计MSE的影响(SNR为15 dB) |
|
图 6 fd对误码率的影响(SNR为15 dB) |
从图 5、图 6可以看出,当最大多普勒频偏fd为0时(信道不变),联合稀疏模型信道估计的MSE、BER性能与图 3、图 4中SNR为15 dB时相吻合,块状导频信道估计方法的MSE、BER性能优于联合稀疏模型.但当信道的最大多普勒频偏fd逐渐增大时,受信道时变的影响,块状导频信道估计方法和所提出的联合稀疏信道估计方法的性能都下降,块状导频信道估计方法性能恶化剧烈,而联合稀疏信道估计方法性能相对下降缓慢,优于块状导频信道估计方法,这是块状导频信道估计方法本身设计上的不足所导致的.当信道变化快时,信道的共稀疏特性发生变化,此时联合多符号的信道估计方法不再适用,信道估计可退化成逐符号信道估计方式.
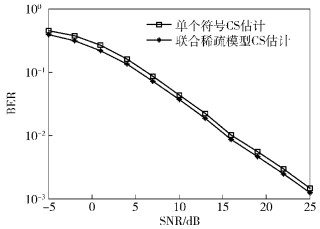
如图 7所示,本研究仿真了在国际电信联盟标准中的短波信道模型iturHFMQ下基于联合稀疏模型的信道估计与逐符号信道估计的性能,该信道是一个两径等功率瑞利衰落信道,两径的时延分别为0 ms和2 ms,每一径幅值服从瑞利分布,其时变多普勒为1 Hz以下.由图 5、图 6所示,由于多普勒频移小,其性能应相当.从仿真结果来看,基于联合稀疏模型信道估计的误码性能比逐符号的信道估计略好.
|
图 7 iturHFMQ信道下不同信道估计方法的BER |
研究了基于压缩感知的OFDM信道估计方法,比较了基于压缩感知的信道估计与传统LS信道估计的性能.利用实际信道响应的时域稀疏特性和相关性,提出了基于联合稀疏模型的OFDM压缩感知信道估计方法,利用若干连续OFDM符号联合估计信道响应.仿真结果表明,基于压缩感知的信道估计性能优于传统LS信道估计性能,大大减小了导频子载波数,而联合多符号的稀疏信道模型压缩感知信道估计进一步改善了逐符号压缩感知信道估计的性能,在信道时变情况下具有更好的性能.
| [1] | Tong Lang, Sadler B M, Dong M. Pilot-assisted wireless transmissions[J].IEEE Signal Processing Mag, 2004, 21(6): 12–25. doi: 10.1109/MSP.2004.1359139 |
| [2] | Coleri S, Ergen M, Puff A, et al. A study of channel estimation in OFDM systems [C]//56th Vehicular Technology Conference (VTC 2002). Vancouver, Canada: IEEE Press, 2002: 894-898. |
| [3] | Hsieh M, Wei C. Channel estimation for OFDM systems based on comb-type pilot arrangement in frequency selective fading channels[J].IEEE Transactions on Consumer Electronics, 1998, 44(1): 217–225. doi: 10.1109/30.663750 |
| [4] |
董秀洁, 王莉, 王素菊. 一种改进的LS信道估计算法[J]. 哈尔滨理工大学学报, 2009, 14(1): 47–50.
Dong Xiujie, Wang Li, Wang Suju. An improved LS channel estimation algorithm[J].Journal of Harbin Uni-versity of Science and Technology, 2009, 14(1): 47–50. |
| [5] | Taubock G, Hlawatsch F, Eiwen D, et al. Compressive estimation of doubly selective channels in multicarrier systems: leakage effects and sparsity-enhancing processing[J].IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 255–271. doi: 10.1109/JSTSP.2010.2042410 |
| [6] | Bajwa W U, Haupt J, Sayeed A M, et al. Compressed channel sensing: a new approach to estimating sparse multipath channels[J].Proceedings of the IEEE, 2010, 98(6): 1058–1076. doi: 10.1109/JPROC.2010.2042415 |
| [7] | Qi Chenhao, Wu Lenan. Optimized pilot placement for sparse channel estimation in OFDM systems[J].IEEE Signal Processing Letters, 2011, 18(12): 749–752. doi: 10.1109/LSP.2011.2170834 |
| [8] | Qi Chenhao, Wu Lenan. Tree-based backward pilot generation for sparse channel estimation[J].Electronics Letters, 2012, 48(9): 501–502. doi: 10.1049/el.2012.0010 |
| [9] | Pakrooh P, Amini A, Marvasti F. OFDM pilot allocation for sparse channel estimation[J].Eurasip Journals on Advances in Singal Processing, 2012(3): 59. |
| [10] | Applebaum L, Bajwa W U, Calderbank A R, et al. Deterministic pilot sequences for sparse channel estimation in OFDM systems[C]//17th International Conference on Digital Signal Processing (DSP). Corfu, Greece: IEEE Press, 2011: 1-7. |
| [11] | Baron D. Wakin M B, Duarte M. Distributed compressed sensing. http://www.ece.rice.edu/-duarte/images/DCS112005.pdf. |
| [12] |
王韦刚, 杨震, 胡海峰. 分布式压缩感知实现联合信道估计的方法[J]. 信号处理, 2012, 28(6): 778–784.
Wang Weigang, Yang Zhen, Hu Haifeng. The method of achieving simultaneous channels estimation on distributed compressed sensing[J].Signal Processing, 2012, 28(6): 778–784. |
| [13] | Tropp J A, Gilbert A C, Strauss M J. Simultaneous sparse approximation via greedy pursuit [C]//IEEE International Conference on Acoustics, Speech and Signal Processing 2005 Proceedings (ICASSP). Philadelphia, USA: IEEE Press, 2005: 721-724. |
| [14] | Barbotin Y, Hormati A, Rangan S, et al. Estimation of sparse MIMO channels with common support[J].IEEE Transactions on Communications, 2012, 60(12): 3705–3716. doi: 10.1109/TCOMM.2012.091112.110439 |


