为了提高低密度奇偶校验码(LDPC)译码器的译码速度, 提出了一种基于部分并行比特选择机制的快速多比特翻转算法.根据接收向量中错误具有随机分布的特点, 将所有比特划分成若干子块, 从每个子块挑选出1个候选翻转比特, 再从这些候选比特中挑选出合理数目的比特进行翻转, 完成译码迭代.此外, 通过引入树形搜索和数据池技术降低该算法核心模块的计算复杂度, 以进一步增加算法硬件实现时的译码速度.分析结果表明, 相较于多比特翻转算法, 利用所提出的算法和相关硬件实现技术, 译码器的吞吐量能得到明显的提高.仿真结果验证了快速多比特翻转算法的有效性.
In order to improve the decoding speed of low density parity check code (LDPC) codes, a fast weighted bit flipping algorithm with partially parallel bit-chosen is proposed. In this scheme, all bits are firstly divided into several blocks according to the stochastic error distribution in the received vector. And then one bit is chosen from each block to form the candidate set of flipped bits. Finally, a proper number of bits are chosen from the candidate set and flipped to implement the decoding. Furthermore, the tree sorting and data pool methods are adopted to decrease the computational complexity of the key module of the proposed algorithm. Compared with the multi-bit flippin (MBF) algorithm by simulations, the proposed scheme and the method of hardware implement can achieve significant improvement in the decoding speed.
低密度奇偶校验码(LDPC,low density parity check code)具有逼近香农限的良好译码性能,得到了广泛的研究.基于位翻转(BF-based, bif flipping based)算法在快速译码方面固有的优势,因此得到广泛的研究[1-2].Ngatched等[3]提出了基于多比特翻转(MBF, multi-bit flippin)算法,获得良好的译码性能及收敛速度.但是,该算法的翻转比特选择机制只能利用串行电路实现,大大地限制了实际构造译码器的吞吐量.
为此,针对接收向量错误随机分布的特点,笔者提出了基于部分并行比特选择机制的快速多比特翻转(FMBF, fast multi-bit flippin)算法,通过降低翻转比特选择时延来提高码字的译码速度, 仿真结果和算法时延分析验证了所提算法的有效性.为了进一步提高译码器的吞吐量,笔者给出了算法核心模块的低时延硬件电路设计方案.
1 MBF及其改进算法笔者使用二进制(N,K)LDPC码字作为研究对象,它的检验矩阵定义为H=[hMN].校验矩阵的行数为M,校验矩阵行、列重分别为γ和ρ. En定义为变量节点n的品质因素,用于衡量该节点的可靠性以决定在译码过程中是否进行翻转.
在MBF算法中,挑选具有最小En值的p个比特节点进行翻转.因为不同的最小值只能串行进行挑选,而且由于受到硬件资源的限制,每个最小值的挑选一般采用部分并行结构实现,这都会使得翻转比特的挑选造成极大的处理延迟.为此,笔者提出了部分并行比特选择机制解决上述问题,详述如下.当信号经信道传输时一般采用交织器将噪声随机化,使得接收向量包含的错误比特服从随机均匀分布.进而,当把接收向量化成若干等长子块时,可以认为错误比特均匀分布在各个子块中.利用错误比特的这一分布特性,笔者提出了一种部分并行比特选择机制:首先将所有比特节点的品质因素划分成p个子块,分别挑选出每个子块中具有最小品质因素En的比特节点作为候选翻转集,然后从候选集中挑选出适当比特进行翻转建议算法与MBF的区别在于翻转比特的选择方法不同,具体描述如下:将N个品质因素分成p个子块,挑选出每个子块最小的品质因素并记录其位置;若q<p, 从p个本地最小值里面挑选出q个具有最小品质因素值的位置进行翻转; 否则, 将所有p个位置进行翻转.
2 硬件模块设计为了进一步提高译码器的译码速度,笔者给出了实现每个校验式上、下可靠性信息查找的min/max树形查找电路、基于数据池的翻转比特选择电路来实现建议算法核心模块的快速计算.
2.1 min/max电路设计如何快速地查找每个校验式的上、下可靠性信息可归结为如何快速确定α个数据中的最大值和最小值.查找一组数的最小值和最大值为一组对称的操作,所需要比较次数相同,利用传统电路都需要作α-1次比较运算.利用文献[4]中的思想,同时完成最小值和最大值的查找,可以明显降低了处理时延和冗余计算,故而有效降低了查找电路的计算复杂度.文中所用到的基本查找单元称为2-mVG,通过将文献[4]中2-mVG的sub-min修改为max得到.类似地,4-mVG等可以通过同样的方法得到.
2.2 翻转比特选择电路翻转比特选择模块的核心功能是实现具有M*(取p或q)个最小品质因素的比特位置的选择.因为各个块的本地最小值是按照时钟顺序串行生成的,因此利用文献[4]中提出的流排序方法首先对前M*个数据进行全排序,之后将完成排序的M*个数据装入数据池中.接下来,利用后续的其他数据对数据池进行更新,即保证每次更新完成之后,池中的数据是已产生的本地最小值中最小M*个.以上操作通过将新输入的数据顺序与池中数据中的数据作比较实现.笔者提出了一种全并行数据插入技术来实现上述要求,即通过M*个比较器同时完成输入数据与池中初始数据的比较,然后将比较器输出的CPi信号送入到由多路选择器构建的选择网络(图 1中基本插入单元电路中的虚框部分)进而得到M*个数据的更新值.图中的输入Ai表示数据池中原有数据,X表示待判定是否进入池中的数据,max和min分别表示上一个基本插入单元中参与比较的两个数据中的较大值和较小值. CL是控制信号,当CL为0时实现最大值的查找,CL为1实现最小值的查找.

|
图 1 基本插入单元 |
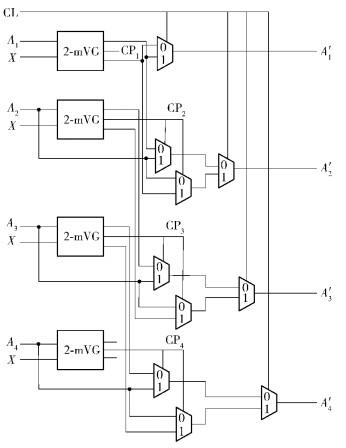
下面讨论翻转位置选择模块中插入电路的具体设计框图(见图 2).为简便起见,以M*=4为例,对利用建议电路实现M*个最小数查找的过程进行详细描述.在查找开始之前,首先令控制信号CL为1①,并且假设前M*个数据已经完成流排序操作,并且按照从小到大的顺序(A1~A4)同时送入4个基本比较单元(前文把2-mVG称为基本比较单元)的输入端口.之后新输入到插入电路的本地最小值X需要同时与上述4个数据进行比较,并且输出相应的CPi信号用于M*个最值的更新.对于第1个比较器,仅需要用A1和X中的较小值来替代A1即可完成最小值更新.对于其余3个比较器,它们的数据更新则取决于CPi的值.如果CPi为1,则需要用前一个比较器输出的较大值来更新Ai,如果CPi为0,则保持Ai,这样就实现了数据的插入.持续上述操作,直至所有N*-M*个本地最小值处理完毕输出数据池中数据就是所需要的M*个全局最小值.对于M*>4的情况,仅需要在现有插入电路的末级增加相应个数的基本插入单元(如图 1所示)就可以简单完成电路的扩展.建议算法里面N*是固定的,M*值是变化的.由于电路的对称性,M*的值只要取N*/2即可完成从N*个数中挑选出任意数目最小值的功能.
|
图 2 基于数据池的插入电路 |
① CL的作用是实现电路查找功能的切换.当CL为0时实现最大值的查找,CL为1时实现最小值的查找.
3 时延分析下面主要对FMBF算法和MBF算法的时延特性进行比较分析.一般LDPC译码器都采用部分并行结构实现[5].笔者也采用这种结构进行2种算法的时延分析.假设2种算法都采用并行度为N/p的硬件单元计算品质因素En.相应地,总共需要p个时钟周期便可以计算出所有比特节点的品质因素.由前述分析可知,数据池的深度最大为品质因素分块数的一半,即N/(2p).数据池经过N/p个时钟周期完成N/(2p)数据全排序过程[4].每个子块最小值的挑选工作可以利用校验式可靠性度量值挑选电路实现(只输出最小值即可),因此经过lb(N/p)个时钟周期输出第1个最小值.由于电路的流水结构,因此总共需要lb(N/p)+p个时钟周期可以求出所有模块的最小值.因为第1个子块的最小值计算出来之后就可以及时送入到数据池查找模块进行处理,并且经过N/p个时钟周期完成N/(2p)数据全排序,再经过N/(2p)将剩余的本地最大值添加到排序序列中,即总共消耗3N/(2p)个时钟周期完成所有翻转位置的挑选.鉴于本地最小值的查找以及数据池操作采用流水结构,使得FMBF算法在每次迭代中完成所有翻转比特位置挑选的总时延为
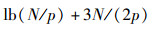
|
(1) |
MBF算法经过lb(N/p)+p个时钟周期完成所有子块本地最小值的挑选,再经过lbp个时钟周期从各个子块最小值中挑选出最小值.在MBF算法中,每次迭代需要挑选λ个具有最小品质因素的比特,且挑选出λ个最小值的过程只能串行执行,MBF算法在每次迭代中完成翻转位置挑选的总时延为

|
(2) |
下面对FMBF和MBF的仿真性能进行分析.仿真使用的码字为EG (1 023,781) 码,为了方便叙述定义为码1.测试数据经过双相移相键(BPSK, binary phase shift keying)调制后经由加性高斯白噪声(AWGN, additive white Gaussion noise)信道传输.每个信噪比(SNR, signal to noise ratio)点观察到100帧错误数据停止译码性能统计.
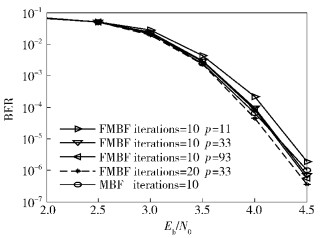
图 3给出了使用FMBF算法以及MBF算法译码的误码率曲线.由图 3可知,FWBF算法在分块数足够大时都可获得与MBF算法相近的误码性能.例如,当码1的分块数取值为33时,FWBF算法与MBF算法在SNR为4.5 dB时的性能差异0.03 dB.另外,FWBF算法在不同分块数下的误码性能随着块数的增加不断提高,当分块数大于一定值后性能差异不大.比如,当分块数为33和11时,两者在SNR为4.5 dB时的误码性能差异为0.15 dB,但分块数33和99的误码性能差异仅为0.02 dB.
|
图 3 FMBF算法以及MBF算法译码性能比较 |
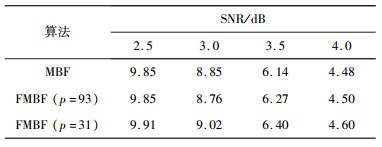
表 1提供了FMBF算法以及MBF算法在最大迭代次数为10时的平均迭代次数.由表 1数据可以看出,随着块数的增加,FMBF算法的平均迭代次数逐渐降低, 不过差值不大,并且差别随着信噪比的增加而逐渐减少.因此,当考虑到硬件资源的限制时,建议使用较小的分块数构造译码器.
|
|
表 1 MBF和FMBF算法的平均迭代次数(N=1 023) |
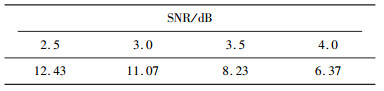
表 2提供了码1在MBF算法译码下,每次迭代的平均翻转比特个数.在并行计算单元取32的情况下,由式(1) 可得FMBF算法译码的处理时延分别为53.此时,利用式(2) 计算出MBF算法的译码时延为42λ.由表 2数据可知,FMBF算法查找翻转比特的时延明显小于MBF算法.比如,在信噪比为4.0 dB时,MBF的一次迭代的平均时延为267.54,而FMBF算法的时延为53,即FMBF算法此时仍获得近5倍的时延降低.
|
|
表 2 码1在MBF算法下的平均翻转比特数(Kmax =10) |
为了进一步提高LDPC译码器的吞吐量,笔者提出了一种基于部分并行比特选择机制的快速MBF算法,并且给出算法关键计算模块的时延优化设计电路用于进一步提高基于本算法构造的LDPC译码器的吞吐量.仿真结果表明,所提算法具有与原始算法近似的译码性能,并且利用笔者设计的算法和硬件电路可以获得译码速度的明显提升.
| [1] |
刘原华, 张美玲. 结构化LDPC码的改进比特翻转译码算法[J]. 北京邮电大学学报, 2012, 35(4): 116–119.
Liu Yuanhua, Zhang Meiling. Improved bit-flipping method for decoding structured low-density parity-check codes[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 116–119. |
| [2] | Liu Z, Pados D A. A decoding algorithm for finite-geometry LDPC codes[J].Communications, IEEE Transactions on, 2005, 53(3): 415–421. doi: 10.1109/TCOMM.2005.843413 |
| [3] | Ngatched T M N. An improved decoding algorithm for finite-geometry LDPC codes[J].Communications, IEEE Transactions on, 2009, 57(2): 302–306. doi: 10.1109/TCOMM.2009.02.060352 |
| [4] | Chin-Long W, Ming-Der shieh, Shin-Yo Lin. Algorithms of finding the first two minimum values and their hardware implementation[J].Circuits and Systems Ⅰ: Regular Papers, IEEE Transactions on, 2008, 55(11): 3430–3437. doi: 10.1109/TCSI.2008.924892 |
| [5] | Wang Zhongfeng, Cui Zhiqiang. A memory efficient partially parallel decoder architecture for quasi-cyclic LDPC codes[J].Very Large Scale Integration (VLSI) Systems, IEEE Transactions on, 2007, 15(4): 483–488. doi: 10.1109/TED.2007.895247 |