2. 中国空间技术研究院 通信卫星事业部, 北京 100094
针对陆地移动卫星系统中体积大、柔性强的星载天线使陆地移动卫星信道传播参数不稳定的问题, 提出由星载天线振颤引起天线指向不精确的陆地移动卫星信道模型.研究复时间序列的衰落统计特性及在振颤临界值范围内对一阶统计特性的影响.仿真结果表明, 天线振颤对所建信道模型的一阶衰落统计特性影响不明显, 而对二阶衰落统计特性影响较大; 在临界值范围内, 对一阶衰落统计特性的影响小到可以忽略; 在精确同步时, 对陆地移动卫星系统的误码率影响较小.
2. Department of Communications Satellite, China Academy of Space Technology, Beijing 100094, China
In order to solve the problems that the propagation parameters instability of land mobile satellite (LMS) channel caused by large volume, strong flexibility of the space-borne antenna for LMS system, a LMS channel model for antenna pointing inaccuracy is proposed from the reason of vibration of space-borne antenna. The fading statistical properties of complex time series and the influence of the first order of statistics characteristics within threshold of the vibration are presented. Simulations show that the vibration of antenna has no obvious effect on first-order statistics properties, but it has great influence on second-order. Within the threshold, the influence on the statistical properties of first order is negligibly small. Considering accurate synchronization, it has little influence on the bit error rate of LMS system.
在陆地移动卫星(LMS, land mobile satellite)系统中,一个准确、有效的LMS信道模型是系统设计的关键. Abele、Arndt等[1-2]在不同场景下研究了窄带LMS传播信道模型;周坡等[3]分析了模型的相关性和可预测性;Hazra S等[4]提出Nakagami_q分布的信道模型,研究模型参数对参考模型的影响;Arndt D等[5]在不同场景下分析半马尔可夫链、仰角和方位角;Konig等[6]估计了C. Loo模型的衰落参数.以上均是在稳定条件下进行的,而天线的不稳定性尤其是柔性天线以某种频率和最大波束中心偏移角振颤而导致模型参数不稳定对信道模型的影响尚未被提出,因此有必要研究振颤下的LMS信道模型.
1 LMS信道建模技术1994年,提出的Corazza信道模型[7]包络的概率密度函数(PDF, probability density function)为

|
(1) |

|
(2) |
其中: k为莱斯因子,σ3、u是阴影遮蔽的标准偏差和均值,I0(·)为第1类零阶修正的贝塞尔函数.
残余累积分布函数(RCDF, residual cumulative distribution function)的理论公式为
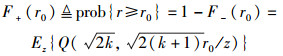
|
(3) |
其中: Ez{·}为z的期望值,Q(A, B)是马克库姆函数.
信号包络的2阶统计特性,如电平通过率(LCR, level crossing rate)和平均衰落持续时间(AFD, average fade duration)分别为
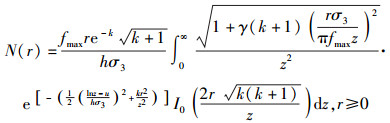
|
(4) |
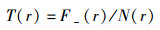
|
(5) |
其中:模型参数k, u, σ3均与移动终端和卫星之间的角度(以下称为卫星仰角)、移动终端所处的阴影环境及频段有关.
2 星载天线振颤下的信道模型研究在L频段的下行通信链路中,同步轨道卫星天线辐射的电磁波在主瓣中的功率分布服从高斯方向图[8-9],本研究选择的高斯方向图分布如下:
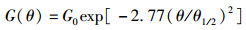
|
(6) |
其中: θ, θ1/2和G0分别为中心角角度、半功率波束宽度、波束中心发射功率增益.高斯方向图表明,星载天线在某一范围内具有较好的波束增益,在波束中心处有最大的辐射功率,且随角度增加辐射功率下降.不稳定的机械特性引起天线指向不精确,使天线辐射功率的变化量超出链路余量而导致信号变形,甚至接收不到卫星发射的信号,产生断连现象.
假设移动终端处的经度和纬度固定,天线周期性地振颤,且天线指向该终端的角度偏移量与持续时间满足指数衰减正弦关系,可表示为
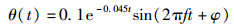
|
(7) |
其中φ、f分别为初始相位和天线振颤频率.天线振颤时的波束中心角变化如图 1所示.
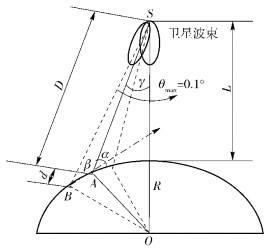
|
图 1 振颤示意图 |
假设γ为振颤前的波束中心角(见式(8));α、β分别为振颤前后的卫星仰角;终端与卫星之间的初始距离D及振颤后的相对移动距离d分别如式(10)、式(11) 所示.
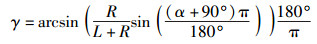
|
(8) |

|
(9) |

|
(10) |
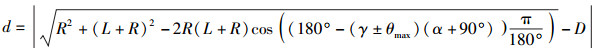
|
(11) |
同步轨道卫星相对于地面“静止”,振颤引起多普勒效应等效为终端运动,其最大多普勒频移为
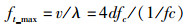
|
(12) |
结合式(9) 和式(12) 得到卫星仰角和最大多普勒频移的变化如表 1所示.
|
|
表 1 卫星仰角和最大多普勒频移的变化 |
在1/4周期内,卫星仰角随波束中心角近似线性增加;最大多普勒频移变化趋势基本一致,且终端处的初始仰角越大,影响越小.在振颤持续时间内,卫星仰角的幅度变化为指数衰减,而最大多普勒频移的变化趋势与天线振颤规律一致.
描述衰落深度、衰落率、衰落持续时间的模型参数是卫星仰角的函数,且二阶统计特性与最大多普勒频移成比例,因此天线振颤对LMS信道有影响.振颤下的信道模型如图 2所示.

|
图 2 振颤下的LMS信道模型 |
参数设置:卫星仰角为20°~80°,步进20°,最大偏移角0.1°,振颤持续100 s,摆动5 s,振颤频率0.2 Hz,3 dB波束宽度0.6°.由最小均方误差准则和最小二乘线性曲线拟合出模型参数,精确的多普勒扩展法[9-10]计算离散多普勒频率、幅度及相位,采用莱斯正弦和[10-11]近似有色高斯噪声随机过程.
3.1 经典的Corazza信道模型的仿真分析图 3示出了振颤对LMS信道RCDF的影响.
|
图 3 振颤下LMS信道模型的1阶统计特性 |
仰角越低振颤对RCDF影响越大,且随着信号能量的减弱,振颤前后误差变小. 图 3(b)与(a)基本一致,表明RCDF仅受卫星仰角的影响,与最大多普勒频移无关.
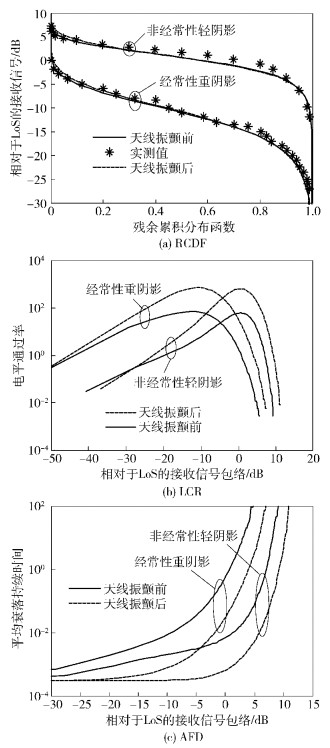
卫星仰角15°时,由于缺乏拟合参数,无法给出仰角与传播参数的关系,仅考虑最大多普勒频移变化对LMS信道模型的影响.在乡村非经常性轻阴影和经常性重阴影环境下,图 4(a)(b)(c)分别给出了RCDF、LCR和AFD,并与实测值[7]及振颤前比较.从图 4可见,振颤引起的最大多普勒频移对RCDF基本没有影响;而衰落率和衰落持续时间变化趋势较大,若对接收信号作归一化处理即可消除最大多普勒频移的影响.
|
图 4 LMS信道模型的1阶、2阶统计特性 |
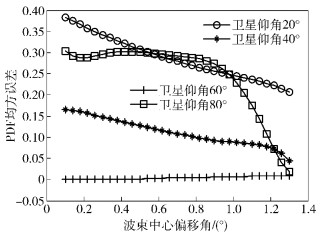
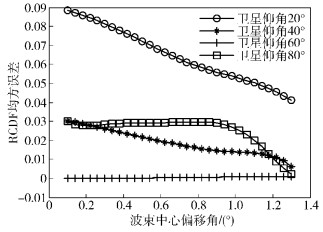
由图 1、式(8) 和式(9) 得出顺时针方向振颤时波束中心最大偏移角的临界值为0.1°~0.47°;逆时针的临界值为0.1°~1.3°.在1/4振颤周期内,以波束中心最大偏移角0.1°作为参考,研究天线沿逆时针方向振颤时对一阶衰落统计特性的影响,其均方误差函数分别如图 5和图 6所示.结果表明,振颤对PDF的影响远大于RCDF;卫星初始仰角在20°~40°之间,振颤影响随波束中心最大偏移角单调递减;而在60°时,天线振颤基本没影响;初始仰角80°时,在某一最大波束中心偏移角处交叉, 表明适当选择卫星仰角能有效地降低振颤对时间序列衰落统计特性的影响.
|
图 5 最大波束中心偏移角对PDF的影响 |
|
图 6 最大波束中心偏移角对RCDF的影响 |
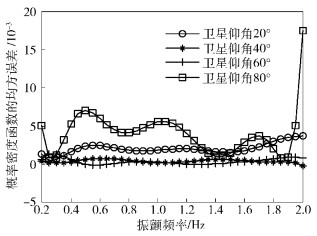
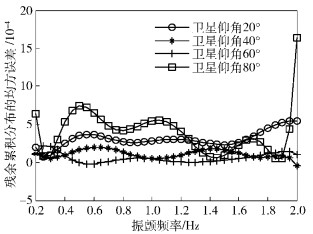
振颤频率越大,卫星天线相对于终端的速度越大,从而产生的最大多普勒频移变化增大.在0.2~2 Hz范围内,临界频率对PDF和RCDF的影响分别如图 7和图 8所示.
|
图 7 振颤频率对PDF的影响 |
|
图 8 振颤频率对RCDF的影响 |
由图可见,天线振颤对PDF和RCDF的均方误差均很小;对PDF的影响在2 Hz达到最大值约为0.001 7,最小值接近0,最大数量级为0.01;对RCDF的影响在达到最大值约为0.000 17,最小值接近0,相比PDF,对RCDF的影响小了一个数量级,达到0.001数量级.
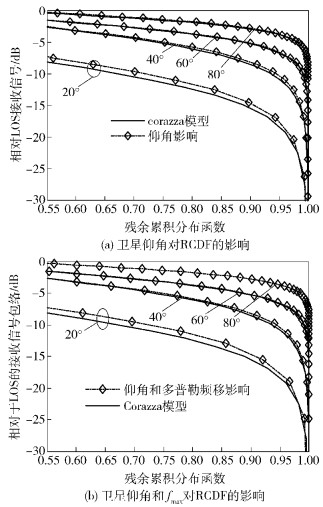
3.3 LMS系统的误码率仿真分析天线振颤产生的多普勒频移会产生乘性噪声,导致信道衰落率和衰落持续时间较大程度变化,由此研究天线振颤对系统可靠性的影响.据GMR-1标准,仿真参数设置为:BCCH逻辑信道传递信息,1/2删余卷积码,CQPSK调制,信道为:天线振颤前后的非经常性轻阴影和经常性重阴影环境下的Corazza信道模型,仿真结果如图 9所示.

|
图 9 振颤对误码率的影响 |
结果表明,在2种信道条件下,与高斯白噪声信道差距较大.随着发射功率的增加,误码性能改善不到两个数量级,这是因为乘性噪声对信号质量影响过大,解调不能还原出信号.同时,在精确同步时,振颤前后的误码率偏差不大,这是因为采用频率跟踪技术,振颤对系统的影响仅来源于卫星仰角的变化,而3.1节表明,卫星仰角变化对信道衰落深度的统计规律基本没影响.
4 结束语静止轨道通信卫星发射天线的不定因素使星载天线以某种频率和波束中心最大偏移角振颤而导致指向不精确, 从而影响信号的传播环境, 是LMS系统非常实际的问题.笔者提出的星载天线振颤下的LMS信道模型能用于真实环境的模拟.仿真结果表明,天线振颤引起的卫星仰角和最大多普勒频移变化会影响LMS信道的衰落统计特性;而在临界值范围内对1阶统计特性的影响小到可以忽略;在精确同步时,对LMS系统可靠性影响较小.若不能完全补偿多普勒频移,天线振颤将使接收机的解调性能降低.
| [1] | Abele A, Perez F F, Bousquet M, et al. A new physical-statistical model of the land mobile satellite propagation channel[C]//2010 Proceedings of the Fourth European Conference on Antennas and Propagation (EuCAP). Barcelona: IEEE Press, 2010: 1-5. |
| [2] | Arndt D, Heyn T, Konig J, et al. Extended two-state narrowband LMS propagation model for S-band[C]//2012 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Seoul: IEEE Press, 2012: 1-6. |
| [3] |
周坡, 曹志刚. 基于马尔科夫过程的卫星移动信道模型及长期预测方法[J]. 电子与信息学报, 2011, 33(12): 2947–2953.
Zhou Po, Cao Zhigang. Markov process based satellite mobile channel model and long term prediction method[J].Journal of Electronics & Information Technology, 2011, 33(12): 2947–2953. |
| [4] | Hazra S, Mitra A. A new land mobile satellite channel model with nakagami-q distribution[C]//2012 National Conference on Communications (NCC). Kharagpur: IEEE Press, 2012: 1-5. |
| [5] | Arndt D, Heyn T, Heuberger A, et al. State modeling of the land mobile satellite channel with angle diversity[C]//2012 6th European Conference on Antennas and Propagation (EUCAP). Prague: IEEE Press, 2012: 3140-3144. |
| [6] | Konig J, Arndt D, Ihlow A, et al. Estimation of fading parameter correlation for modeling the land mobile satellite channel[C]//2012 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Seoul: IEEE Press, 2012: 1-5. |
| [7] | Corazza G E, Vatalaro F. A statistical model for land mobile satellite channels and its application to nongeostationary orbit systems[J].IEEE Transactions on Vehicular Technology, 1994, 43(3): 738–742. doi: 10.1109/25.312773 |
| [8] | John D K, Ronald J M. Antennas: for all applications, third edition[M]. [S.l.]: The McGraw-Hill Companies, Inc, 2002: 17-82. |
| [9] | 郭庆, 王振永, 顾学迈, 等. 卫星通信系统[M]. 北京: 电子工业出版社, 2010: 94-107. |
| [10] | Patzold M, García R, Laue F. Design of high-speed simulation models for mobile fading channels by using table look-up techniques[J].IEEE Transactions on Vehicular Technology, 2000, 49(4): 1178–1190. doi: 10.1109/25.875225 |
| [11] | Patzold M, Killat U, Laue F. A deterministic digital simulation model for suzuki processes with application to a shadowed rayleigh land mobile radio channel[J].IEEE Transactions on Vehicular Technology, 1996, 45(2): 318–331. doi: 10.1109/25.492906 |



