2. 燕山大学 河北省特种光纤与光纤传感重点实验室, 秦皇岛 066004
针对无线传感器网络无标度容错拓扑的级联失效问题, 首先借助概率母函数法, 推导出单一随机节点失效下无线传感器网络无标度容错拓扑的级联失效规模, 进而在幂函数负载分布条件下, 求解出触发无线传感器网络无标度容错拓扑级联失效的临界负载值.研究结果表明, 在无线传感器网络无标度容错拓扑中, 当网络负载参数超过其临界值时, 一个随机故障节点将引起整个网络的级联失效.仿真结果验证了解析推导的正确性.
2. The Key Laboratory for Special Fiber Sensor of Hebei Province, Yanshan University, Hebei Qinhuangdao, China
In view of cascading failure problem of scale-free fault tolerant topology in wireless sensor networks, the scale of cascading failure caused from one random fault node is deduced based on the probability generating function. The critical load value of the cascading failure is discovered under the condition of power function load distribution. The research result shows that a random fault node will cause cascading failure of the entire network when the load parameter exceeds its critical value. Simulations verify the correctness of the analytical derivation.
有限的节点容量和负载的重新分配使得一个节点的失效会导致其他节点的级联失效.网络一旦发生级联失效,往往具有很强的破坏力.近年来,学者们利用无标度拓扑(度分布服从幂律分布)对随机节点失效的强容错能力,有效提升了无线传感器网络(WSNs,wireless sensor networks)的容错性能.但是这种强容错性是在假设一个节点的失效不会引起其他节点失效的前提下成立的.为此,WSNs无标度拓扑级联失效问题成为当前亟待解决的科学问题.
针对无标度拓扑级联失效问题,Motter等[1]提出了负载-容量级联失效模型,解释了级联失效产生的原因. Dobson等[2]推导了无标度拓扑中的级联失效规模,用分支过程法解析出了产生级联失效的临界容量条件.李勇等[3]采用概率母函数法研究了容量均匀分布物流保障网络的级联失效问题,得到了网络级联崩溃的临界容量值. Wang等[4]和Dou等[5]就线性和非线性的节点容量分布,也给出了缓解级联失效的最优容量. Liu等[6]通过容量优化提升了无标度拓扑对级联失效的抵抗能力.总体而言,对于无标度拓扑级联失效问题,人们不仅关注拓扑的级联失效规模,更关心的是拓扑的级联失效承载极限.但已有研究均立足于用节点容量优化来提升无标度拓扑抵抗级联失效的能力.然而受有限资源和恶劣环境的制约,真实无线传感器网络中节点容量是固定的,动态分配容量抵制网络级联失效设想在WSNs中是不合理的.
正是出于上述考虑,这里根据WSNs无标度容错拓扑的负载和容量分布特点,建立起WSNs无标度容错拓扑的级联失效模型,并推导出触发WSNs无标度容错拓扑级联失效的临界负载值,为WSNs无标度容错拓扑级联失效优化研究提供理论依据.
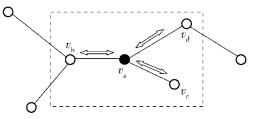
1 级联失效模型图 1所示为WSNs无标度容错拓扑的级联失效过程.
|
图 1 级联失交过程示意图 |
结合图 1可知,WSNs无标度容错拓扑的级联失效模型包含以下5个步骤.
1) 网络G中,节点vi, i=1, 2, …, N的负载为li,所有节点具有相同容量C.
2) 在初始时刻有1个随机节点失效.
3) 如果vj, j=1, 2, …, N失效,将其负载均匀分配给其邻节点,邻节点vi的负载为li(Λ)=li+lj/kj,其中li(Λ)为vi的新负载,kj为vj的度.
4) 对于所有的节点vi, i=1, 2, …, N,测试其负载li(Λ).若li(Λ)>C,则vi失效,转至第3) 步.
5) 如果所有的节点vi, i=1, 2, …, N都有li(Λ)≤C,则级联失效过程结束.
2 级联失效的临界负载考虑到WSNs无标度容错拓扑中一个随机失效节点可能引发网络级联失效问题.首先利用概率母函数法推导出WSNs无标度容错拓扑在随机节点失效下的级联失效规模S.再依据级联失效临界规模阈值Sthreshold确定出触发WSNs无标度容错拓扑大规模级联失效的临界负载值.
2.1 级联失效规模根据WSNs无标度容错拓扑的度分布p(k)可得,概率母函数为

|
(1) |
其中kmin和kmax分别为网络中节点的最小度和最大度.
由随机选择1条边连接到度为k的节点,并且该节点是失效节点的概率可表示为
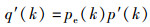
|
(2) |
其中: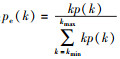
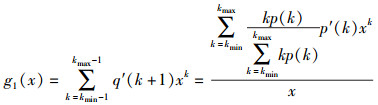
|
(3) |
故由随机选择的一条边所引发的级联失效规模,可以按照由这条边达到节点的剩余度分为不同情况:到达节点剩余度为0,级联失效规模为1.到达节点剩余度为1,级联失效规模为到达节点连接的连通分支规模加1.依此递推,可得由随机选择一条边所引发的级联失效规模的概率的概率母函数为

|
(4) |
从而由一个随机失效节点所引发的级联失效规模的概率母函数为

|
(5) |
即由一个随机失效节点所引发的级联失效规模为

|
(6) |
由于网络连通和覆盖服务质量与网络级联失效规模S直接关联[7],所以根据不同的应用需求给定不同的级联失效规模阈值Sthreshold.当S>Sthreshold时,网络无法保证连通和覆盖服务,出现了大规模级联失效.也就是说,对于随机节点失效情况,S=Sthreshold是网络出现大规模级联失效的临界点.
基于S=Sthreshold,下面确定WSNs无标度容错拓扑(p(k)=αk-β, (α>0, 2<β<3))中节点的临界负载值.由于节点的负载存在差异,故障节点对邻节点失效的影响程度是不同的.为此,式(2) 可写为
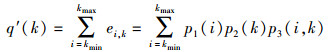
|
(7) |
其中:p1(i)为随机选择度为i的节点的概率,p1(i)=αi-β;p2(k)为由随机选择的一条边连接到度为k的节点的概率,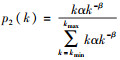

将式(7) 代入式(3), 有
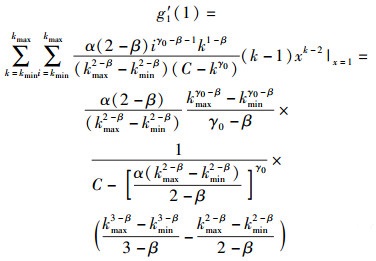
|
(8) |
又由式(1) 得
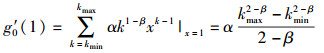
|
那么由一个随机失效节点所引发的WSNs无标度容错拓扑级联失效规模(式(6))可表示为
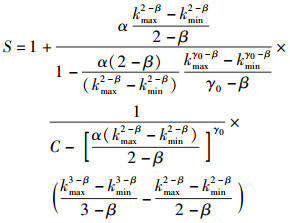
|
(9) |
在WSNs无标度容错拓扑度分布p(k)=αk-β(kmax= 

|
(10) |
其中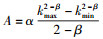

|
给定N=100,度分布p(k)=1.94k-2.92(kmax=10, kmin=1),Sthreshold=N/5,C=10的WSNs无标度容错拓扑(记为拓扑1),采用图解法对超越方程式(10) 求解,得到触发该网络级联失效的节点临界负载值γ.
根据式(10) 可得,A=1.855 2,B=3.189 2.那么,式(10) 可写为

|
(11) |
记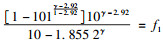
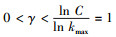
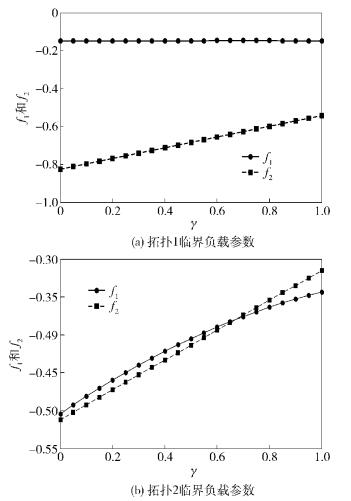
|
图 2 拓扑1和拓扑2临界负载参数值γ示意图 |
类似给定N=100,度分布p(k)=2.15k-2.60(kmax=10, kmin=1),Sthreshold=N/5,C=10的WSNs无标度容错拓扑(记为拓扑2).同样采用图解法对触发该网络级联失效的节点临界负载值γ进行求解.
根据式(10) 可得,A=0.540 1,B=4.361 4.那么,式(10) 可写为
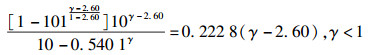
|
(12) |
记


下面通过Matlab仿真验证理论临界负载参数值的合理性.采用度分布可调WSNs无标度容错拓扑控制算法[8](DDA,degree distribution adjusted),分别生成节点数N=100,度分布p(k)=1.94k-2.92(kmax=10, kmin=1) 的WSNs无标度容错拓扑1和节点数N=100,度分布p(k)=2.15k-2.60(kmax=10, kmin=1) 的WSNs无标度容错拓扑2.这里,分别对拓扑1和拓扑2进行100次的随机节点移除,统计负载参数γ在(0, 1) 区间内变化时,拓扑1和拓扑2的级联失效规模S变化过程. 图 3显示了拓扑1和拓扑2级联失效仿真结果平均值.
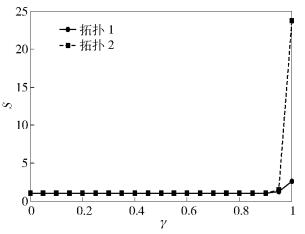
|
图 3 拓扑1和拓扑2临界负载参数γ的仿真图 |
由图 3可见,随着负载参数γ的递增,拓扑1和拓扑2的级联失效规模均呈递增趋势,且拓扑2的级联失效规模增长速度大于拓扑1.此外,在整个γ取值范围内,拓扑1始终没有发生大规模级联失效,但在γ


利用概率母函数法给出了在幂函数负载分布条件下触发WSNs无标度容错拓扑级联失效的临界负载值.实例分析和仿真结果较好地说明了该理论计算临界负载值的正确性.下一步将要研究的问题包括,提升临界负载值的精度,以及采用临界负载值研究WSNs无标度容错拓扑级联失效优化问题,以避免WSNs无标度容错拓扑出现大规模级联失效的危害.
| [1] | Motter A E, Lai Y C. Cascade-based attacks on complex networks[J].Phys Review E, 2002, 20(2): 1–11. |
| [2] | Dobson I, Carreras B A, Newman D E. A probabilistic load-dependent model of cascading failure and possible implications for blackouts[C]//HICSS-36, Hawaii: IEEE, 2003: 1-10. |
| [3] |
李勇, 吴俊, 谭跃进. 容量均匀分布的物流保障网络级联失效抗毁性[J]. 系统工程学报, 2010, 25(6): 853–860.
Li Yong, Wu Jun, Tan Yuejin. Invulnerability study for cascading failure of the logistics support networks of capacity evenly distributed[J].Journal of Systems Engineering, 2010, 25(6): 853–860. |
| [4] | Wang Jianwei, Li Lirong. A model for cascading failures in scale-free networks with a breakdown probability[J].Physica A, 2009, 388(1): 1289–1298. |
| [5] | Dou Binglin, Wang Xueguang, Zhang Shiyong. Robustness of networks against cascading failures[J].Physica A, 2010, 389(1): 2310–2317. |
| [6] | Liu Yuanni, Li Xin, Chen Shanzhi, et al. Model for cascading failures based on the nodes with different tolerance parameter[J].Journal of China Universities, 2011, 18(5): 95–101. |
| [7] |
尹荣荣, 刘彬, 刘浩然. 新的无线传感器网络拓扑容错性测度[J]. 北京邮电大学学报, 2013, 36(1): 95–100.
Yin Rongrong, Liu Bin, Liu Haoran. Novel measure of topology tolerance for wireless sensor networks[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(1): 95–100. |
| [8] |
郭进利, 汪丽娜. 幂律指数在1与3之间的一类无标度网络[J]. 物理学报, 2007, 56(10): 5635–5639.
Guo Jinli, Wang Lina. Scale-free networks with the power-law exponent between 1 and 3[J].Acta Physica Sinica, 2007, 56(10): 5635–5639. doi: 10.3321/j.issn:1000-3290.2007.10.014 |


