为了实现在系统总人数大于基站发送天线数条件下, 对多小区系统中小区间和小区内用户干扰同时抑制的目的, 提出一种基于迫零算法的分布式波束成形的用户选择算法.算法将整体用户分为可一同参与迫零算法和不可一同参与的两类, 并利用信道之间的弦距去选择可一同参与迫零算法的用户, 实现波束成形向量与未参与迫零的本地信道之间的准正交, 同时分析和证明了该算法的有效性.仿真结果表明, 新算法在不同发送天线数和总用户数条件下, 其吞吐率性能均优于传统算法.
In order to suppress both the intra-cell interference and the inter-cell interference in the multi-cell system, a user selection method of the distributed beamforming based on zero-forcing algorithm is proposed. The users are selected with the chord distance between channels, and the base station utilizes these users' channels to implement zero-forcing algorithm and achieve beamforming vectors. Simulations show that under condition of different transmitting antenna number and the users' numbers, the throughput rate of the proposed algorithm becomes superior to the traditional ones'.
在分布式多小区多输入多输出(MIMO,multiple input multiple output)正交频分复用系统中,各个基站具有较高的独立性,无需或需要较少的协作,避免了由于基站间完全信道信息共享所引起的基站间大量信息反馈和交互负担的问题.因此本研究关注多小区分布式波束成形. Jorswieck等[1]提出了基于线性预编码的多小区波束成形算法,虽然可以实现分布式处理,基站间无需数据交互,但场景是每小区只有一个用户,仅考虑小区间干扰,忽略了小区内用户干扰.文献[2-3]针对小区间和小区内干扰同时存在场景,提出了基于迫零算法(ZF, zero forcing)的波束成形算法,但要求基站发送天线数不小于系统总人数, 文献[4]还要求基站发送天线数不小于每小区人数,但在现实系统中这些条件较为苛刻. Jang等[5]提出了一种在基站发送天线数小于系统总人数条件下多小区波束成形算法(UJ,u jang),此算法将小区间和小区内干扰同时考虑,然而在选择参与ZF算法的用户时,从基站的角度将不同小区用户严格区分开,并分配固定的名额,这大大限制了算法操作的灵活性,并没有充分利用ZF算法去抑制小区间干扰.
目前,针对小区间和小区内用户干扰同时存在且系统总人数大于基站发送天线数的多小区场景研究较少,因此提出一种基于ZF算法的分布式波束成形用户选择算法.算法将用户分为可一同参与ZF算法和不可一同参与的两类,然后再利用信道的相似性去选择参与ZF算法的用户.该算法不仅无需将用户严格地按照不同小区区别开,又不针对某一小区分配固定的参与ZF算法的名额,比较充分地利用了ZF算法,而且可以实现对小区间和小区内用户干扰同时抑制.
1 系统模型考虑一个由小区k和k′构成的下行MIMO传输两小区系统,每个小区中的基站有Nt个发射天线,且包含M个用户,每个用户仅由所在小区的基站服务且配备1个接收天线.在小区k中第i个用户k(i)接收到的有效和干扰信号可以表达为
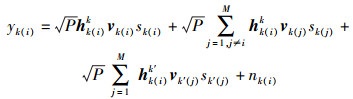
|
(1) |
其中:hk(i)k∈C1×Nt表示从基站k到用户k(i)下行信道向量,系统中信道相互独立等概产生且均为瑞利衰落信道,同时假设信道向量的模的期望是相等的;vk(i)∈CNt×1为用户k(i)的波束形成向量;sk(i)是用户k(i)的能量归一化目的信号;nk(i)为均值为0,方差为1的加性高斯白噪声.为简化分析,假设各用户间是等功率发送的,且每个用户的发送功率均为P.
2 基于ZF的分布式波束成形2.1 问题的描述首先将从基站k到所有用户的下行信道定义为基站k的本地信道,即hk(j)k和hk′(j)k, j=1,2,…,M.同理hk(j)k′和hk(j)k′, j=1,2,…,M就是基站k′的本地信道.为了满足分布式系统模型的要求,假设基站k仅可以获得自己的本地信道信息.同时,基站k′也仅可以获得其自己的本地信道信息.
当Nt ≥2M时,在基站k处,根据ZF算法有

|
令Φk(i)代表与k(i)一同参与ZF算法的用户集合,此时Φk(i)包含系统内所有用户,即
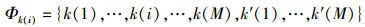
|
当Nt<2M时,由于Φk(i)至多包含Nt个用户,因此Φk(i)无法包含系统内所有用户,于是就有C2MNt个不同的Φk(i),其中存在C2M-1Nt-1个包含用户k(i)的Φk(i).与此对应,就有C2M-1Nt-1个Hk(i),定义为Hk(i)(j), j=1, 2, …, C2M-1Nt-1,则
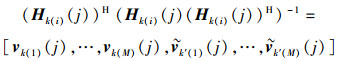
|
于是对于k(i)来说就存在vk(i)(j), j=1, 2, …, C2M-1Nt-1.定义向量集合Ωk(i)={vk(i)(j), j=1, 2, …, C2M-1Nt-1},则用户k(i)需要从Ωk(i)中选择合适的向量,来优化自己的吞吐率.又由于‖hk(i)kvk(i)(j)‖=1, j=1, 2, …, C2M-1Nt-1,在每个用户等发送功率的条件下,用户k(i)的吞吐量则由来自其余用户的干扰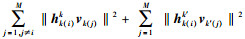

|
(2) |
从用户k(i)的角度,可以将其余所有用户分为两类:一类是与k(i)一同参与基站k的ZF算法的用户,若用ϕk(i)(j)代表此类集合中的第j个用户,那么Φk(i)={ϕk(i)(j), j=1, 2, …, Nt}.另一类就是没有与k(i)一同参与基站k的ZF算法的用户,若用Φk(i)和ϕk(i)(n)分别代表此类用户集合以及集合中的第n个用户,那么Φk(i)={ϕk(i)(n), n=1, 2, …, 2M-Nt},其中|Φk(i)|=2M-Nt,则问题(2) 可以改写为
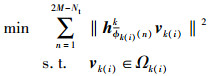
|
(3) |
在Nt<2M条件下,本研究提出一种无须计算Ωk(i)的用户选择算法,利用本地信道之间的相似度来选择合适的用户,从而组成式(3) 的最优解所对应的用户集合Φk(i).具体算法步骤如下.
1) 初始化
Φk(i)=∅,Uk(i) =∅, 令G-k(i)表示除了k(i)之外的所有用户的集合,G-k(i)(m)是G-k(i)中第m个用户,G-k(i)={G-k(i)(m), m=1, 2, …, 2M-1}.
2) 得到Uk(i)的过程如下.
For m=1:2M-1
① 基站k计算hG-k(i)(m)k与其余本地信道hG-k(i)(n)k, n=1, 2, …, 2M-1, n≠m的相似度,并求和
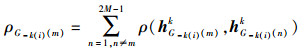
|
其中相似度
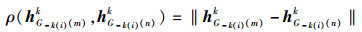
|
② 将ρG-k(i)(m)存入Uk(i), Uk(i)←Uk(i)∪{ρG-k(i)(m)}
End
3) 得到用户集合Φk(i)的过程如下.
For j=1: Nt-1
① 从Uk(i)中选出最小值项,并将其对应的用户G-k(i)(m)记为ϕk(i)(j),存入Φk(i), 即

|
② 将ρϕk(i)(j)和ϕk(i)(j)从集合Uk(i)和G-k(i)中分别除去.
③ 除去已选用户的对当前Uk(i)的影响,避免干扰对下一个用户的选择.
For m=1:|G-k(i)|
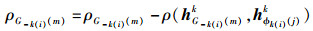
|
End
End
4) 根据Φk(i)得到Hk(i)Φ,再进行ZF算法.
2.3 算法的分析与证明令建议算法的解是vk(i)o_ZF. Γk(i)代表k(i)的参与ZF的任一用户集合,且Γk(i) ≠Φk(i),并根据Γk(i)得到Hk(i)Γ. vk(i)φ_ZF是Hk(i)Γ经ZF算法得到的k(i)的波束成形向量,Γk(i)与φk(i)(n)分别代表没有与k(i)一同参与基站k的ZF算法的用户集合以及其中第n个用户,即Γk(i)={φk(i)(n), n=1, 2, …, 2M-Nt}.如果式(4) 成立,那么就可以说明提出算法是有效的.
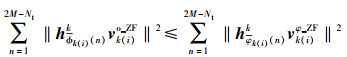
|
(4) |
由于各个信道是独立等概产生的,可以近似认为干扰‖hϕk(i)(n)kvk(i)o_ZF‖2, n=1, 2, …, 2M-Nt也是独立等概率出现的,则式(4) 可以等效写为
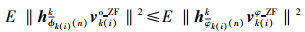
|
(5) |
下面证明式(5) 成立.
证明 根据所提出的算法,容易得到已知条件
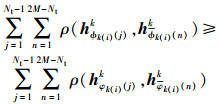
|
为了便于证明,在此用向量夹角的余弦代表向量之间的相似度(弦距),可以得到

|
其中:θϕ(j, n)为hϕk(i)(j)k与hϕk(i)(n)k向量夹角, θφ(j, n)为hφk(i)(j)k与hφk(i)(n)k向量夹角,因为各个信道是独立等概率产生的,那么向量之间的夹角也是独立等概率的,所以有
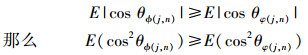
|
(6) |
定义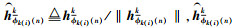
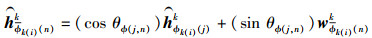
|
其中:wϕk(i)(n)k是在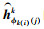
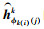

|
那么
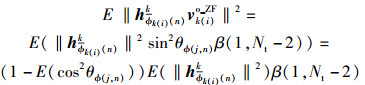
|
同理
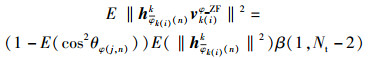
|
再根据式(6) 可得
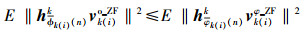
|
则式(5) 成立,所以提出的算法是有效的.
定义一次信道相似性运算的复杂度分别为Ψd.每个本地信道需要进行2(M-1) 次相似性运算,对应运算复杂度2(M-1)Ψd,提出算法的运算复杂度主要来自于信道之间相似性的运算量,那么提出算法的运算复杂度近似为2(2M-1)(M-1)Ψd.
3 仿真结果与分析仿真场景为2个小区,每基站发送天线数一致,每用户单天线,采用瑞利块衰落信道,信道估计接近理想信道估计,噪声为零均值且方差为1的高斯白噪声.
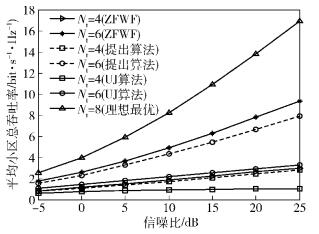
如图 1所示为每小区用户数M=4的条件下,提出算法与UJ算法和功率注水ZF算法(ZFWF,ZF water filling)分别在不同发送天线数Nt下的平均小区总吞吐量的性能对比结果.当Nt逐渐增大,越来越多的用户可同时参与ZF算法, 而UJ算法受限于固定的小区内外用户名额,性能受到影响.当Nt=8时,达到Nt=2M临界条件,所有用户均可同时参与ZF算法,小区间和小区内干扰可同时消除,所以吞吐率得到较大的提升.
|
图 1 M=4用户平均小区总吞吐率的对比 |
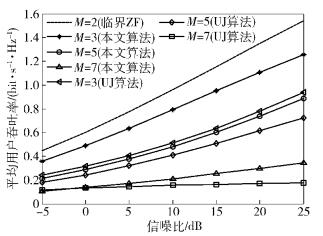
由图 2可以看出,当Nt固定时,随着每小区用户数M的增加,用户间干扰也逐渐增大,对于同一种算法的平均用户吞吐率是下降的,但由于提出算法并不严格区分小区内外用户,可以选择与其余本地信道较近似的本地信道所对应的用户,在相同的M条件下,本地算法比UJ算法要有更高的平均用户吞吐率.当M=2时,达到临界条件Nt=2M,所有用户可同时参与迫零,无须再进行用户选择算法,每个用户受到的小区内和小区间的干扰可以同时完全消除,所以其用户平均性能也是最好的.
|
图 2 Nt=4平均用户吞吐率的对比 |
针对发送天线数小于总用户数且小区间和小区内用户干扰同时存在的场景,提出了一种基于ZF算法的分布式波束成形的用户选择算法.该算法利用信道之间的相似度去组成参与ZF算法的用户集合,从而可将ZF算法有效地应用于分布式系统.并分析和证明了该算法的有效性,仿真结果表明该算法吞吐率性能优于传统算法.
| [1] | Jorswieck E, Larsson E, Danev D. Complete characterization of the Pareto boundary for the MISO interference channel[J].IEEE Trans on Signal Processing, 2008, 56(10): 5292–5296. doi: 10.1109/TSP.2008.928095 |
| [2] | Kim K, Lee J. Coordinated beamforming with limited BS cooperation for multicell multiuser MIMO broadcast channel[C]//Vehicular Technology Conference (VTC 2009). Barcelona: IEEE Press, 2009: 1-5. |
| [3] | Kim H, Yu H, Youngchul Sung, et al. An efficient algorithm for zero-forcing coordinated beamforming[J].IEEE Communications Letters, 2012, 16(7): 994–997. doi: 10.1109/LCOMM.2012.050412.112565 |
| [4] |
程铁铮, 袁超伟, 解芳. MIMO广播系统中的用户丢弃准则[J]. 北京邮电大学学报, 2009, 32(3): 27–31.
Cheng Tiezheng, Yuan Chaowei, Xie Fang. User rejection criterion under MIMO broadcast system[J].Journal of Beijing University of Posts and Telecommunications, 2009, 32(3): 27–31. |
| [5] | Jang U, Son H, Park J, et al. CoMP-CSB for ICI nulling with user selection[J].IEEE Trans on Wireless Communications, 2011, 10(9): 2982–2993. doi: 10.1109/TWC.2011.072511.101661 |
| [6] | Jindal N. MIMO broadcast channels with finite-rate feedback[J].IEEE Trans on Information Theory, 2006, 52(11): 5045–5060. doi: 10.1109/TIT.2006.883550 |


