针对传统的多径信道下零前缀正交频分复用(ZP-OFDM)系统符号盲同步方法的估计精度低的问题, 提出一种ZP-OFDM系统的符号盲同步新方法.该方法基于ZP-OFDM符号中零前缀的功率出现规律性的分布特性, 利用不等长双窗口能量检测的办法进行符号盲同步.仿真结果表明, 在多径信道下, 该符号盲同步方法不但具有良好的估计精度而且不受载波频率偏移的影响.
The traditional blind symbol synchronization scheme for zero prefix orthogonal frequency division multiplexing (ZP-OFDM) could not acquire accurate symbol synchronization estimation over multipath channels. According to this problem, a new blind symbol synchronization scheme for ZP-OFDM systems was proposed. The proposed scheme is based on zero prefix power collection in the ZP-OFDM symbols whose ZP average power regularly distributes in the two slide windows, and is applied the energy detection method of two unequal length windows to realize the blind symbol synchronization. Simulations show that the proposed symbol synchronization estimation scheme is not only of good estimation precision but also is not influenced by carrier frequency offset over multipath channels.
随着近年来零前缀(ZP, zero prefix)取代循环前缀(CP, cyclic prefix)的正交频分复用(OFDM, orthogonal frequency division multiplexing)调制方法的提出,ZP-OFDM系统受到了越来越多的关注与重视[1-2].在ZP-OFDM系统中,符号定时同步影响到了该系统的抗载波间干扰性能和解调输出的误码率等因素,使其成为了该系统需要解决的关键性问题之一[3-4].在非合作通信中,由于信号的先验信息未知,无法从接收信号中提取导频、训练序列等辅助数据,也没有发射端的配合参与,所以基于非辅助数据的ZP-OFDM系统定时同步的研究具有一定的意义.因此笔者重点研究非合作通信中多径衰落信道下ZP-OFDM系统的符号盲同步方法.
目前对于ZP-OFDM系统的符号盲同步方法研究较少,Le N V等[3]提出一种多径衰落信道下ZP-OFDM系统的符号同步方法,但该方法仅适应于定时误差的粗估计并且估计性能较差.文献[4]利用双滑动窗能量比检测的办法估计ZP-OFDM系统的符号同步,但是该方法不仅受信道影响较大,还需要较为精准的信道估计和足够的ZP冗余度,因此在实际通信系统中较难实现.针对这些问题,提出了一种多径衰落信道下ZP-OFDM系统的符号盲同步方法.
1 ZP-OFDM系统模型设发送端发送的ZP-OFDM符号的有效数据长度为N,零前缀长度为Nc,符号总长度为Nt=N+Nc,则第m个符号经过快速傅里叶逆变换(IFFT, inverse fast fourier transform)后输出的信号可表示为[3]
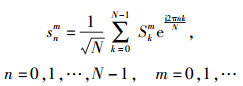
|
(1) |
其中Skm为第k个子载波上调制后的基带数据.加入零前缀后,输出信号可表示为
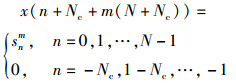
|
(2) |
再经高斯噪声的影响后,则表达式为
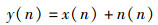
|
(3) |
在多径信道下,设输入长度为N+L-1的序列{xk, xk-1, …, xk-N-L+2},经过多径最大时延为L,信道冲击响应为{h0, h1, …, hL}和噪声为{nk, nk-1, …, nk-N+1}的信道后,输出序列可用矩阵表示为

|
(4) |
则信道的记忆特性使得能量均值d(n)的表达式为
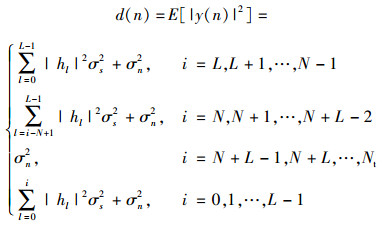
|
(5) |
其中:σs2为信号功率,σn2为噪声功率.
2 ZP-OFDM系统的符号盲同步方法2.1 传统方法及其缺陷在对接收到的ZP-OFDM信号进行符号盲同步之前,需要对接收信号的符号总长度Nt和P段长度进行盲估计[5],然后再进行后续处理.在文献[4]中,利用如图 1所示长度为M(M≤Nc)的滑动窗口A和滑动窗口B,其能量表达式为
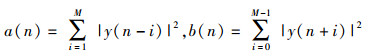
|
(6) |

|
图 1 滑动窗检测符号同步模型 |
并对上述滑动窗能量作比值,可得m(n)的表达式为
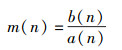
|
(7) |
根据式(7),m(n)的均值在当n=0处可取到峰值,最后通过寻找峰值对符号定时误差进行估计.
以上方法忽略了窗口B在多径信道中的变化,并且会出现信噪比越高,定时误差估计的准确率越低的情况.因此,针对这些缺陷,通过设计窗口B和窗口A,并且计算能量叠加值的比值来选取峰值的位置,从而进行定时误差的估计.
2.2 窗口B的设计针对窗口B,进行了分步设计思路.首先设计窗口长度为N并进行能量叠加,即
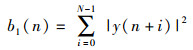
|
(8) |
其中能量叠加值b1(n)的均值可推导为
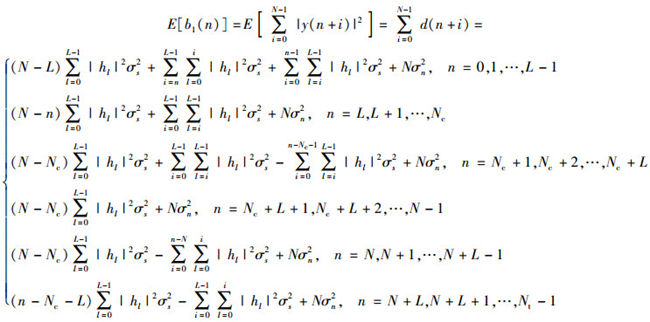
|
(9) |
但是这样使得估计出的定时误差值的期望可能向右偏移,且能量叠加值b1(n)值会在定时误差右侧形成缓变过渡带,不便于直接提取误差值.
然后设计前L长度的能量值和中间N长度的能量值进行叠加,即
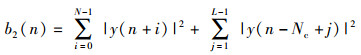
|
(10) |
则能保证估计出的定时误差值的期望不会向右偏移,可弥补b1(n)的不足.其中能量叠加值b2(n)的均值可推导为

|
(11) |
且该值较小,则使能量叠加值b2(n)在初始位置左侧会形成长度为L的平缓地带,失去了尖峰特性,定时信息也不便于提取.
最后,为了充分利用窗口B的值,将之前设计的两种不同方法所得的能量累加值b1(n)和b2(n)进行相乘运算,则表达式为
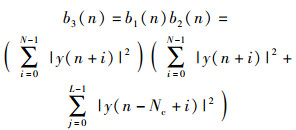
|
(12) |
能量叠加值b3(n)使得初始点的尖峰特性得以凸显.
2.3 窗口A的设计基于信道估计难度的考虑,本研究对窗口A也进行了改进.针对于窗口A,也进行了分步设计思路,首先设计窗口长度为Nc-L并进行能量叠加,即
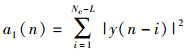
|
(13) |
其中能量叠加值a1(n)的均值可推导为
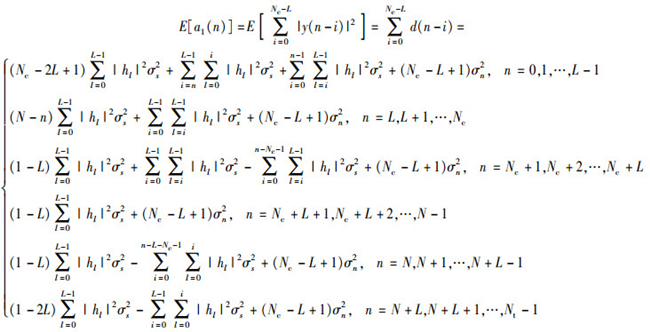
|
(14) |
但是该设计方法所得能量叠加值a1(n)在初始位置左侧具有平缓特性.
然后设计窗口A长度为Nc进行能量叠加,可得
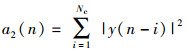
|
(15) |
其中能量叠加值a2(n)的均值可推导为

|
(16) |
这样会使得能量叠加值a2(n)在初始位置右侧也具有缓变过渡带.
最后,为了充分利用窗口A的值,将之前设计的两种不同方法所得的能量累加值a1(n)和a2(n)进行相乘运算,则其表达式为
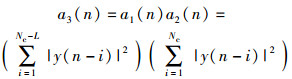
|
(17) |
能量叠加值a3(n)使得初始点的尖峰特性得以凸显.
在对窗口B和窗口A进行设计之后,根据式(12)、式(17) 和式(7),将所得到的窗口乘积值进行比值运算,其表达式为
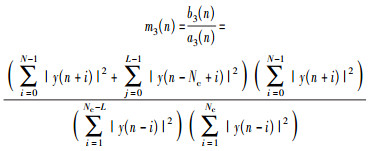
|
(18) |
为了验证提出方法的有效性,通过Matlab仿真软件进行仿真实验,其仿真条件为:载波个数N为64个,1/4的零前缀长度,符号周期T=10 μs,采样频率为8 MHz,具有一对相关导频的OFDM信号作为信号源,信道选用SUI-1信道、TU6信道和指数衰落信道3种多径信道类型,蒙特卡洛仿真次数为1 000次,性能采用估计正确率P进行评估,其表达式为
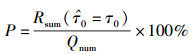
|
(19) |
其中:τ0表示准确的定时误差值,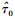
图 2所示为所提出的方法在不同信道下符号定时估计的正确率曲线.从图 2中可以看出,在多径信道下,所提方法不但有效可行并且对信道具有较高的普适性.
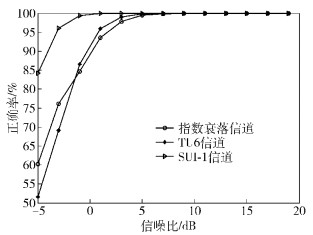
|
图 2 不同信道下性能曲线 |
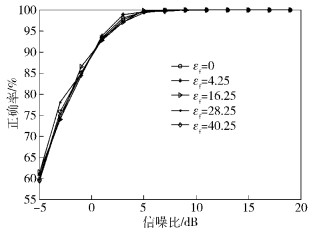
图 3为所提方法在指数衰落信道中,不同的相对频率偏移εf情况下符号定时估计的正确率曲线.从图 3中可以看出,剩余频偏εf对所提方法的估计性能影响不大.由此说明,提出的符号定时盲同步方法具有更好的稳健性.
|
图 3 不同相对频移下性能曲线 |
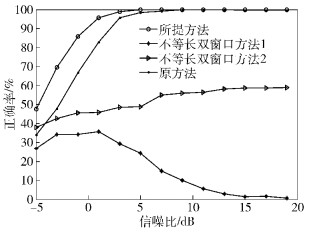
为了更好地验证提出方法的性能,将提出的最佳方法和不等长双窗口方法1、不等长双窗口方法2与文献[4]中的原方法进行性能对比实验.其中,不等长双窗口方法1是将N长度的窗口B与Nc-L长度的窗口A的能量叠加并进行比值的方法;不等长双窗口方法2是将N长度的窗口B与Nc长度的窗口A的能量叠加并进行比值的方法,其性能对比图如图 4所示.从图 4中可以看出,在TU 6信道下,当信噪比大于等于-5 dB时,所提方法的估计正确率高于不等长双窗口方法1、不等长双窗口方法2和文献[4]中的原方法.随着信噪比的提高,所提方法、不等长双窗口方法2和原方法的估计性能也随着提高,但不等长双窗口方法1随着信噪比的增加,估计性能反而有所下降,这是由于不等长双窗口方法1的定时误差估计是有偏估计,其结果的均值不是所求的误差位置.
|
图 4 TU6径衰落信道下性能对比曲线 |
| [1] | Van W T, Le N V, Duplicy J, et al. Analytical expressions for power spectral density of CP-OFDM and ZP-OFDM signals[J].IEEE Signal Processing Letters, 2010, 17(4): 371–374. doi: 10.1109/LSP.2010.2040651 |
| [2] | Dai Linglong, Wang Zhaocheng. Spectrum-efficient coherent optical zero padding OFDM for future high-speed transport networks[C]//Global Communications Conference (GLOBECOM), 2012 IEEE. Anaheim, USA: IEEE press, 2012: 2896-2900. |
| [3] | Le N V, Van W T, Duplicy J, et al. Blind coarse timing offset estimation for CP-OFDM and ZP-OFDM transmission over frequency selective channels[J].EURASIP J. Wireless Commun. Networking, 2009, 44(1): 1–6. |
| [4] |
李长青, 刘丹谱, 乐光新. ZP-OFDM系统在多径信道下的符号盲同步方法[J]. 北京邮电大学学报, 2006, 29(6): 115–119.
Li Changqing, Liu Danpu, Yue Guangxin. A blind symbol synchronization for ZP-OFDM systems in multipath Channel[J].Journal of Beijing University of Posts and Telecommunications, 2006, 29(6): 115–119. |
| [5] |
刘明骞, 李兵兵, 唐宁洁. 多径信道下ZP-OFDM信号的时域参数盲估计[J]. 系统工程与电子技术, 2011, 33(11): 2531–2535.
Liu Mingqian, Li Bingbing, Tang Ningjie. Blind ZP-OFDM time-parameters estimation in multipath Channel[J].Systems Engineering and Electronics, 2011, 33(11): 2531–2535. doi: 10.3969/j.issn.1001-506X.2011.11.35 |


