无碰撞区跳频序列集的汉明相关函数在相关区内为零, 可以消除跳频多址扩频系统中跳频信号在无碰撞区的相互干扰.基于矩阵置换提出了一种最大汉明相关值可灵活设定的无碰撞区跳频序列集的一般构造方法, 该方法构造得到的跳频序列集具有较低的最大汉明相关值和较长的无碰撞区长度.作为一般构造法的一个特例, 介绍了移位构造法.
For the frequency hopping sequence sets with no-hit zone, the values of their Hamming correlation functions in the no-hit zone equal to zero, which can be used to eliminate the mutual interference in a frequency-hopping code-division multiple-access communication system. Based on the matrix permutation, a general construction of frequency hopping sequence sets with no-hit zone and flexible maximum Hamming correlation value is presented in this paper. Using the proposed method, frequency hopping sequence sets with lower hamming correlation and longer no-hit zone can be obtained. In addition, as a special case of the general method, a construction based on cyclic shift is introduced.
与常规跳频序列集的设计不同, 无碰撞区跳频序列集要求汉明相关函数在相关区内等于零[1-2].其意义在于, 即使在传送的跳频序列间存在相对时延, 但只要相对时延不超过一定的范围(碰撞区), 那么不同序列之间的碰撞数仍然为零, 从而可以消除相互干扰.使用无碰撞区跳频序列, 可以设计准同步跳时/频(time-hopping/frequency-hopping)码分多址(CDMA, code division multiple access)系统, 它在超宽带无线电系统多用户雷达和声纳系统等领域具有潜在的应用价值[3].
近年来, 国内外学者致力于具有良好性能的跳频序列的设计研究, 构造出了大量参数达到或接近理论界的、最优的低碰撞跳频序列, 但其中关于无碰撞区跳频序列集的构造研究成果还比较有限[2, 4-7].
基于矩阵置换, 文献[8]给出了一种最优无碰撞区跳频序列集的构造.在此基础上, 本研究将进一步给出一种最大汉明相关值可灵活设定的无碰撞区跳频序列集的一般构造方法.基于此方法可得到最大汉明相关值较低而无碰撞区长度较长的跳频序列集.与已有的构造方法相比, 笔者提出的方法的优点是最大汉明相关值可预先设定、单条序列或序列集为最优, 而且参数可灵活选取、构造方法多样.其次, 作为一般构造法的特例, 介绍移位构造法, 证明了它具有比一般构造法更特殊的性质, 并给出实例.
1 基本定义和性质令「x 
定义1 设F={f0, f1, …, fq-1}表示q个可用频点的字符集, X=(Xt), Y=(Yt)表示F上的2个长度为N的序列, 0≤t < N.则序列X与Y之间的汉明互相关函数和序列X的汉明自相关函数分别定义如下:
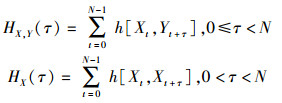
|
其中
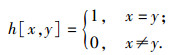
|
定义2 设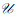
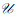

|
定义3 设S⊆ 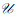
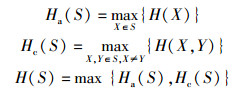
|
关于跳频序列及跳频序列集合,分别有如下的理论.
引理1[9] 设F为一字符集, 且|F|=q,对字符集F上任意长度为N的序列X, 有
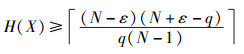
|
其中ε=(N)q.若等号成立,称序列为最优跳频序列.将上式的右边记为λ1,若H(X)=λ1+1,则称序列为几乎最优跳频序列.
引理2[10] 设S为F上含M条长度为N的序列的集合,|F|=q,则
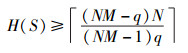
|
若等号成立,称序列集为最优跳频序列集.将上式的右边记为λ2,若H(S)=λ2+1,则称序列集为几乎最优跳频序列集.
定义4 设S为F上的M条长度为N的跳频序列组成的集合, 则序列集S的自相关无碰撞区ZANH、互相关无碰撞区ZCNH和无碰撞区ZNH分别定义如下:
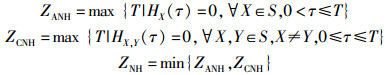
|
当ZNH > 0,则称S为无碰撞区跳频序列集,记为(q, N, M, ZNH; λ),其中q为频点个数,N为序列长度,M为序列条数,ZNH为无碰撞区长度,λ为S的最大汉明相关值.
对无碰撞区跳频序列集(q, N, M, ZNH; λ),其参数也受理论界的限制,满足[2]

|
若等号成立,则序列集称为最优无碰撞区跳频序列集.若
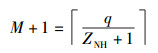
|
则称为几乎最优无碰撞区跳频序列集.
定义5[7] 设X=(Xt)是一个长度为N的跳频序列,0≤t≤N-1,若对任意的0≤s≠t≤N-1,有Xs≠Xt,则称X为无重复跳频序列.
2 无碰撞区跳频序列集的新构造首先给出最大汉明相关值为n的无碰撞区跳频序列集的一般构造法,并分析其最优性质;其次作为此构造法的一个特例,介绍移位构造法.
构造1 设F={f0, f1, …, fq-1}为q个可用频点的字符集, q=M(N+N′), N≤M, M > 1, N≥1, N′≥1.构造包含如下步骤:
1) 将F中的频点排成M×N矩阵和M×N′矩阵,分别记为P0、P1.记P0的第i列为Xi,0≤i≤N-1;
2) 在P0中任取n列,1≤n≤N,记为Xl0, Xl1, …, Xln-1,0≤l0 < l1 < … < ln-1≤N-1;剩余的N-n列记为Xl′0, Xl′1, …, Xl′N-n-1, 0≤l′0 < l′1 < … < l′N-n-1≤N-1;
3) 对0≤i≤n-1, 令σ为{0, 1, …, M-1}上的置换, 定义Xli上的置换πli为

|
对0≤i≤N-n-1,设σi为{0, 1, …, M-1}上的置换, 定义Xl′i上的置换πl′i为
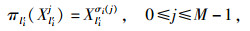
|
且σ0(j), σ1(j), …, σN-n-1(j)两两不相等, σ(j)≠σi(j), 0≤i≤N-n-1;
4) 现分别对P0中的Xl0, Xl1, …, Xln-1进行置换πli,0≤i≤n-1,分别对Xl′0, Xl′1, …, Xl′N-n-1进行置换πl′i,0≤i≤N-n-1,置换后得到的新矩阵记为P2;
5) 最后,以矩阵P0P1P2的每一个行向量为一条序列,构造序列集S,表示如下
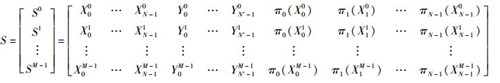
|
定理1 上述构造的序列集S为(M(N+N′), 2N+N′, M, N-1;n)序列集.
证明 由于P0→P2为仅进行列置换的矩阵置换,故当且仅当移位τ=N和τ=N+N′时序列集S中才会发生碰撞,所以S的无碰撞区大小为N-1,并且当τ=N时碰撞发生在P2中,当τ=N+N′时,碰撞发生在P0中.下面仅探讨τ=N+N′时的情况,当τ=N时的情况可类似讨论.
当τ=N+N′时,对0≤a1, a2≤M-1,
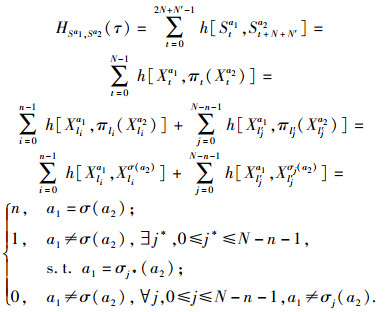
|
类似可得

|
因此,S为(M(N+N′), 2N+N′, M, N-1;n)序列集.证毕.
注意,上述构造中的n可根据要求自由选取,即由构造1可构造出最大汉明相关值可灵活设定的无碰撞区跳频序列集.由于在应用中希望最大汉明相关值较小,下面讨论几种最佳情形.
性质1 当N=M, N′=1时,构造1给出的序列集为几乎最优无碰撞区跳频序列集.
证明
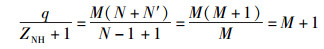
|
由定义可知,构造1给出的序列集为几乎最优无碰撞区跳频序列集.
性质2 若H(S)=1,即n=1, 则构造1得到的序列集S为最优跳频序列集;若H(S)=2,则S为几乎最优跳频序列集.
证明 由引理2,有
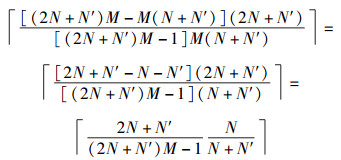
|
因为N≥1, N′≥1, M≥2,所以

|
又因为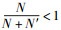

|
若H(S)=1,则
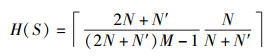
|
即S为最优跳频序列集;
若H(S)=2,则
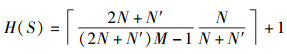
|
即S为几乎最优跳频序列集.证毕.
注:当H(S)=1时,显然有H(S; L)=1,此时还可以验证S是严格最优跳频序列集.关于严格最优的定义及性质,可以参考文献[11].
对S中单条序列,当πli, 0≤i≤n-1为非单位置换的情况比较无规律,难以定性研究,下面仅考虑πli为单位置换的情形.这里约定N, N′不同时为1.由于πli为单位置换,故S中每条序列的频点个数为q′=2N+N′-n,则S中每条序列Si的最大汉明自相关值H(Si)=n,0≤i≤M-1,所以Si要最优必须满足

|
其中ε=(2N+N′)q′.
因为2N+N′=2N+N′-n+n=q′+n,故
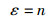
|
所以
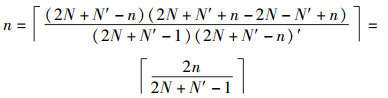
|
即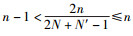

|
所以当n=1或2时,Si为最优跳频序列.于是,有以下性质.
性质3 在构造1中,设πli,0≤i≤n-1,为单位置换,且N, N′不同时为1,当n=1或2时,S中每条序列都是最优的.
注:特别地,当n=1时,可以验证S中每条序列还是严格最优的.
作为上述一般构造法的一个特例,下面介绍移位构造法,并分析由此得到的序列集的一些最优性质,最后给出一个实例.
构造2 对构造1中的P0的Xl′0, Xl′1, …, Xl′N-n-1进行循环移位:Lτl′i(Xl′i), 0≤i≤N-n-1.对Xl0, Xl1, …, Xln-1进行循环移位:Lτli(Xli),0≤i≤n-1.这里,0≤τl′0, τl′1, …, τl′N-n-1≤M-1两两不同,0≤τl0=τl1=…=τln-1≤M-1,且τli≠τl′j,0≤j≤N-n-1,得到新矩阵记为P′2,以矩阵P0P1P′2的每个行向量为序列,构造序列集R,表示如下
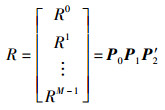
|
定理2 构造2得到序列集R的参数为(M(N+N′), 2N+N′, M, N-1;n).
事实上,由于移位构造法是一般构造法的一个具体特例,因此得到的序列集R当然是(M(N+N′), 2N+N′, M, N-1;n)序列集.但注意到,移位构造法除了满足上述性质1~3外,本身还具有如下一些特有的性质.
性质4 在构造2中,当τli≠0时,若存在j*, 0≤j*≤N-n-1,使得τl′j*=0,则R中每条序列都是最优的,且为1碰撞序列,即H(Ri)=1;若对任意的j, 0≤j≤N-n-1,有τl′j≠0,则R中每条序列也是最优的,且为无碰撞(重复)序列,即H(Ri)=0.
证明 相关性质的证明类似于定理1,这里从略.关于当条序列的最优性,注意到,若存在j*,0≤j*≤N-n-1,使得τl′j*=0,则R中每条序列的频点个数q″=2N+N′-1.若对任意的j,0≤j≤N-n-1,有τl′j≠0,则R中每条序列的频点个数q″=2N+N′.由引理1易证.
例 令F={f0, f1, …, f24},M=5,N=4,N′=1,将F按顺序排成一个5×5矩阵,记为Q′0,分别记此矩阵中的第1, 2, 3, 4列为X1, X2, X3, X4,对X1, X2, X3, X4分别进行如下循环移位:L1(X1), L2(X2), L3(X3), L4(X4),得到一个新的5×4矩阵,记为Q′1.以矩阵Q′0Q′1的每个行向量为序列,构造序列集R如下
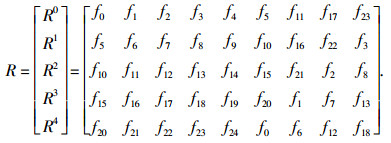
|
则易验证序列集R为每条序列都为无碰撞(重复)序列的无碰撞区大小为3的几乎最优无碰撞区跳频序列集,且每条序列都是最优的.
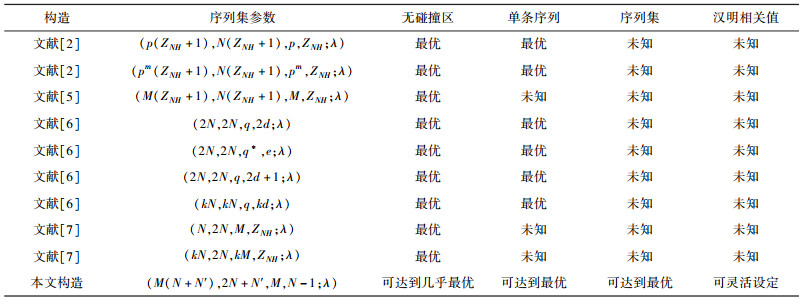
3 结束语本研究给出一种无碰撞区跳频序列集的一般构造方法,其优点是最大汉明相关值可预先设定,使得单条序列或序列集为最优,其中的一些性质是已有的构造法不具有的(见表 1).并且基于此构造法得到的序列集参数可灵活选取、构造方法多样.由此得到的序列集汉明相关值较低而无碰撞区长度较长,是一类相关性能较好的序列集.
|
|
表 1 已有的无碰撞区跳频序列集与本研究结果比较 |
| [1] | Ye Wenxia, Fan Pingzhi. Two classes of frequency hopping sequences with no-hit zone[C]//Proc 7th Intl Symp Commun Theory Appl. Ambleside, UK: IEEE Computer Society, 2003: 304-306. |
| [2] | Ye Wenxia, Fan Pingzhi. Construction of non-repeating frequency-hopping sequences with no-hit zone[J].Electron Lett, 2006, 42(8): 681–682. |
| [3] | Zeng Qi, Peng Daiyuan, Wang Xiaoning. Performance of a novel MFSK/FHMA system employing no-hit zone sequence set over rayleigh fading channel[J].IEICE Transactions, 2011, 94-B(2): 526–532. |
| [4] | Wang Xiaoning, Fan Pingzhi. A class of frequency hopping sequences with no-hit zone[C]//Proc 4th Intl Conf par Dist Comp. Appl Tech. Chengdu: Southwest Jiaotong Univ, 2003: 896-898. |
| [5] | Ye Wenxia, Fan Pingzhi. Construction of frequency hopping sequences with no hit zone[J].Journal of Electronics(China), 2007, 24(3): 306–307. |
| [6] | Chung Jin Ho, Han Yun Kyoung, Yang K. No-hit-zone frequency-hopping sequence sets with optimal hamming autocorrelation[J].IEICE Trans Fundamentals, 2010, E93-A(11): 2239–2244. doi: 10.1587/transfun.E93.A.2239 |
| [7] |
孙国杰. 交织法构造无碰撞区跳频序列集[J]. 光通信研究, 2012, 5(173): 68–69.
Sun Guojie. Interleaving technique-based construction of NHZ frequency hopping sequence set[J].Study on Optical Communications, 2012, 5(173): 68–69. |
| [8] |
陈浩源, 柯品惠, 张胜元. 基于矩阵置换的最优无碰撞区跳频序列集的构造研究[J]. 计算机应用, 2013, 33(11): 3028–3031.
Chen Haoyuan, Ke Pinhui, Zhang Shengyuan. Construction of optimal frequency hopping sequence sets with no-hit zone based on matrix permutation[J].Journal of Computer Applications, 2013, 33(11): 3028–3031. |
| [9] | Lempel A, Greenberger H. Families of sequence with optimal Hamming correlation properties[J].IEEE Info Theory, 1974, 20(1): 90–94. doi: 10.1109/TIT.1974.1055169 |
| [10] | Peng Daiyuan, Fan Pingzhi. Lower bounds on the Hamming auto-and cross-correlations of frequency-hopping sequences[J].IEEE Trans on Information Theory, 2004, 50(9): 2149–2154. doi: 10.1109/TIT.2004.833362 |
| [11] | Zhou Zhengchun, Tang Xiaohu. New classes of frequency-hopping sequences with optimal partial correlation[J].IEEE Trans Inf Theory, 2012, 58(1): 454–455. |