提出了基于最优用户选择的协作频谱感知方案, 通过引入Gerschgorin圆盘理论建立用户选择机制, 筛选出信道条件最优的若干个认知用户, 由其对应的感知数据空间生成全局判决统计量以实现最优协作感知, 并在此基础上提出迭代门限算法, 进一步优化感知性能.理论分析和仿真结果表明, 该方案无需知晓授权用户信号、信道、噪声功率等先验信息, 对噪声功率不确定性具有较强的鲁棒性, 且当接收机采样次数和参与协作的用户数都受限时, 感知性能仍然很稳定, 可作为协作频谱感知的现实可实现方案.
Gerschgorin disk theorem based optimal user selection algorithm is proposed for cooperative spectrum sensing. The fusion center receives the sensing data from the secondary users and establishes the optimal user selection mechanism by employing Gerschgorin disk theorem. The sensing data of the selected secondary users will subsequently be fused as the global test statistic. Aided by the optimal user selection strategy, the cooperative sensing performance can be ameliorated. Furthermore, the detection performance can also be improved through the proposed iterative thresholding algorithm. Theoretical analysis and simulation results show that the algorithm depends on no a priori knowledge of the primary user signal and the noise power. The proposed method is hence robust against the noise power uncertainty, and can maintain consistent performance when slightly fewer sampling data and users are involved in cooperative sensing.
认知无线电(CR, cognitive radio)[1]作为新兴的动态频谱接入技术,对授权频段(LFB, licensed frequency bands)占用状态的实时监测和跟踪是CR系统认知环节中最根本、最重要的先决环节.由于认知用户(SU, second user)接入LFB时相对于授权用户(PU, primary user)的从属地位,要求SU尽可能少地对PU产生干扰和影响.因此,研究高性能、最优化、易实现的频谱感知方法具有十分重要的意义.
为了提高协作感知的性能,软数据融合(SDF, soft data fusion)方案得到了广泛研究[2-4].参与协作感知的SU将各自的感知数据发送给融合中心(FC, fusion center),FC根据感知数据生成全局判决统计量(GTS, global test statistic)并最终完成判决.现有文献中,协作感知一般都由全部SU参与GTS生成,而在实际感知场景下,由于地理位置、环境分布等因素影响,各个SU在本地感知性能方面可能存在很大差异.如何在所有SU的集合中选定参与协作的最优用户子集,以提高全局感知性能,成为协作感知需解决的一个核心问题.
本文主要针对SDF设计了基于Gerschgorin圆盘理论[5](GDT, gerschgorin disk theorem)的最优用户选择(OUS, optimal user selection)协作感知方案,将感知数据空间在Gerschgorin圆盘域上进行圆盘集合分离,并且在感知协方差矩阵的Gerschgorin酉变换矩阵基础上提出GDT优化算法(GDTO, GDT optimazation),以提高频谱感知性能.
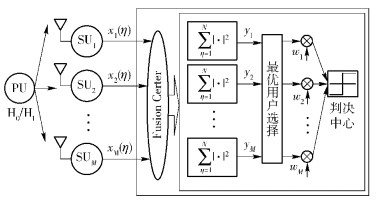
1 系统模型CR协作网络由一个FC和M个参与协作的SU构成,其系统模型如图 1所示.各SU将其原始感知数据发送至FC,FC完成OUS得到最优用户选择向量w=[w1, w2, …, wM]T,并筛选出最优用户子集,最终融合其感知数据生成GTS,实现全局判决.
|
图 1 CR协作频谱感知系统模型 |
PU信号存在与否采用二元假设H0/H1表示.假设PU信号结构及干扰、噪声等信息都完全未知,第i个SU接收机在频谱感知时间段内进行N次采样得
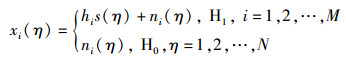
|
(1) |
其中:s(η)为PU发射机发出的信号,hi为PU发射机与第i个SU接收机之间的信道系数,ni(η)为高斯白噪声,满足ni(η)~CN(0, δn, i2),且与s(η)相互独立. 图 1中,第i个SU感知数据为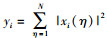
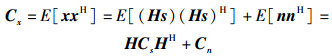
|
(2) |
其中Cs和Cn表示PU和噪声信号对应的自相关矩阵. x=[x1(η), x2(η), …, xM(η)]T,n=[n1(η), n2(η), …, nM(η)]T,s=[s(η-L+1), s(η-L+2), …, s(η)]T,L为M个SU接收信号所对应的最大的多径延迟路径数目,信道系数矩阵为H=[h1, h2, …, hM]T并且hi=[hi1, hi2, …, hiL]T.实际中基于有限次信号采样获得估计采样协方差矩阵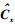
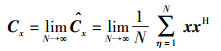
|
(3) |
根据文献[6],理想协方差矩阵Cx有M′(1≤M′≤M)个较大特征值,并具有如下性质:
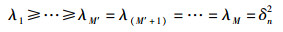
|
(4) |
H0和H1下的Cx对应表示为Cx, i(i=0, 1),在N受限的情况下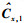
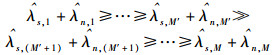
|
(5) |
由式(5) 知协方差矩阵由特征分解得到信号分量和噪声分量,前M′个SU接收到PU信号强度较大,而剩下M-M′个SU接收到PU信号的衰减程度较大,在H1下观测数据几乎等同于噪声观测数据.
文献[2]提出一种等效于能量检测(ED, energy detection)的等增益合并(EGC, equal gain combination)算法,其GTS为
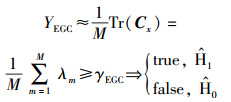
|
(6) |
其中γEGC表示EGC算法的判决门限.
笔者提出GDTO算法,通过引入GDT来筛选最优用户子集,推导出最优用户选择向量w,用于筛选出最优SU感知数据生成最优GTS.协作感知能量值集合为Z={y1, y2, …, yM},按升序排列得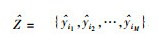
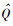
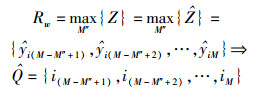
|
(7) |
由式(7) 可得w的第i个选择元素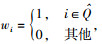
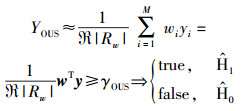
|
(8) |
其中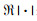
基于GDT提出了OUS协作频谱感知算法.一般地,由于感知数据有限性,对于高阶矩阵很难精确计算其特征值,但可通过GDT得出Gerschgorin圆盘半径和圆心,实现对特征值范围的估计.设n阶复数矩阵A=(aij)且A∈Cn×n,在复数平面上,集合
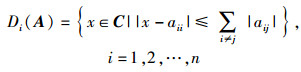
|
(9) |
为矩阵A的第i个圆盘.矩阵A的特征值在n个圆盘的并集中,A的所有圆盘的并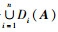
由式(5) 可知,协作感知需要筛选出M′个最优用户的感知数据用于融合,而使用GDT可实现不同圆盘的分离,圆盘可以确定特征值的大致范围,使得GDT可用于筛选最优用户.下面考虑使用Gerschgorin酉变换来有效地解决圆盘重叠问题,更好地分离圆盘,完成最优用户的筛选. Gerschgorin酉变换的步骤如下:
步骤1 Gerschgorin酉变换首先需将矩阵Cx分块:
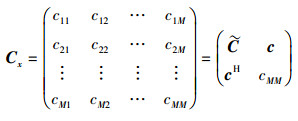
|
(10) |
步骤2 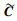
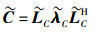
|
(11) |
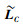
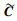
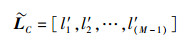
|
(12) |
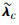
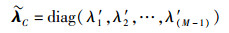
|
(13) |
步骤3 由以上分析得到酉变换变换矩阵L:
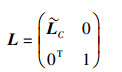
|
(14) |
协方差矩阵Cx酉变换之后得到酉变换矩阵U:

|
(15) |
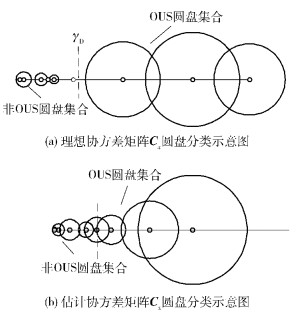
根据酉变换矩阵U,可得M-1个圆盘的圆心和半径,圆盘分类示意图如图 2(a)所示,其中SU圆盘圆心大于判决门限值γD即(γi > γD)的圆盘判为OUS圆盘,并纳入最优用户子集,反之则判决为非OUS圆盘.
|
图 2 圆盘分类示意图 |
根据Gerschgorin酉变换的步骤,估计协方差矩阵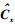

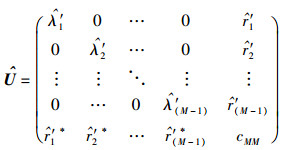
|
(16) |
相应的Gerschgorin酉变换矩阵
基于信息论准则(ITC, information theory criterion)的盲协作感知算法[7]的典型代表为AIC算法和MDL算法,具体函数表达式如下:
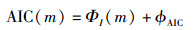
|
(17) |
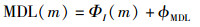
|
(18) |
其中,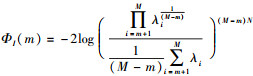
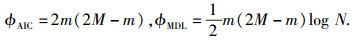
|
将实际中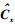
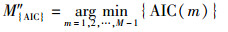
|
(19) |
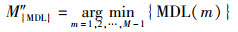
|
(20) |
当函数取最小值时,得到最优协作用户数M″,并推导出最优用户选择向量.同理,可以推导出GLE算法中GAIC(gerschgorin AIC)和GMDL(gerschgorin MDL算法的函数表达式分别为
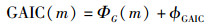
|
(21) |
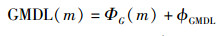
|
(22) |
其中,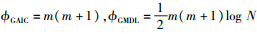
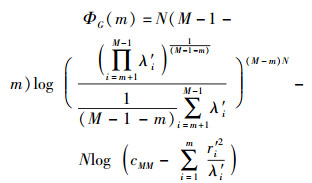
|
将协方差矩阵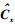
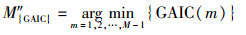
|
(23) |
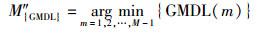
|
(24) |
针对GLE算法的局限性和不足,提出Gerschgorin圆盘估计算法(GDE, gerschgorin disk estimated),它是通过对圆盘半径的迭代比较最终确定GDE门限值,以实现协作频谱感知尽可能少的依赖先验信息的目的. GDE算法通过GDE门限值区分Gerschgorin圆盘空间中不同信道条件的SU.由U得出Gerschgorin圆盘半径,N越大圆盘半径越准确,同时得出GDE门限值也就越精确.定义GDE算法判决方程如下:
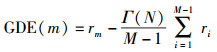
|
(25) |
其中,m是[1, M-1]之间的整数,Γ(N)取值为[0,1],随N增加呈递减趋势[5].从m=1开始迭代估计直到取得第一个非正值时取得GDE门限值,高于门限值的圆盘被纳入最优用户子集,反之被淘汰. GDE只需要对得到的圆盘半径进行迭代比较得出判决门限完成最优用户子集的筛选,对先验信息的依赖性较低.
3.3 迭代门限算法在无须PU信号及噪声功率先验信息的条件下,OUS算法可以实现对PU信号的有效感知.在OUS算法基础上,结合式(6)(8) 可以准确地完成判决.然而,当GTS位于OUS门限值和EGC门限值之间时,极易造成FC误判.对此问题,提出迭代门限算法(ITA, iterative thresholding algorithm),有效地解决了噪声过大或PU信号衰落严重的情况.此算法结合了OUS和EGC的优点,根据不同的GTS采用ITA算法完成判决.
ITA通过充分利用所有SU的感知数据,结合EGC算法生成GTS,首先采用EGC算法的判决门限值γEGC和OUS算法的判决门限值γOUS进行初判决,若YEGC大于γOUS则采用OUS方案判决,若YEGC小于γEGC则采用EGC方案判决.在尽可能少地依赖先验信息的条件下自适应地确定门限值.一般地,噪声信号强度比PU信号要小,可从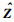
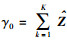

|
(26) |
其中,φi为自适应门限值系数,γi是在第i次迭代中,满足不等式条件时所截取得到的ITA门限值.根据PFA, DES确定门限系数如下:
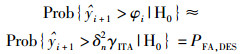
|
(27) |
由此可见,ITA判决门限值的获取是根据实时采样信号作出的判决,可以有效地改善噪声功率不确定性的影响,使用门限值γITA完成ITA的判决方程为
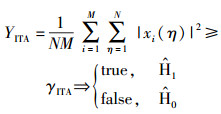
|
(28) |
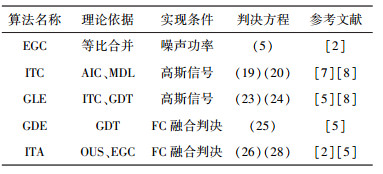
综上所述,ITA算法在继承EGC感知算法简捷、易实现的基础上提高了感知性能.对于可以进行准确判决的区域直接判决,而介于判决门限值之间的GTS,需要对FC融合数据重新判决. 表 1为所提出的OUS协作频谱感知算法与EGC算法的对比.
|
|
表 1 OUS协作频谱感知算法对比 |
利用Matlab仿真,设定M=10,N=2 000,PFA, DES=0.1.考虑信噪比SNR范围为[-20 dB, -2 dB].对于EGC算法仿真中分别取噪声不确定度Δ=0,Δ=1①作出EGC算法感知性能曲线.
① EGC算法需考虑噪声功率作为先验条件,估计噪声功率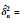
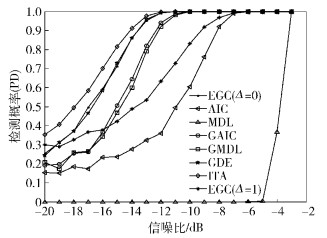
仿真1 在协作CR系统环境中仿真GDTO算法、EGC算法以及ITA算法,并作出不同信噪比下的性能比较如图 3所示:EGC感知算法在噪声功率理想已知即Δ=0时感知性能相对较好,但在Δ=1时性能很差,虚警概率很高. GDTO算法通过筛选出最优SU的感知数据生成GTS,其中,GLE算法明显改善了传统ITC算法的性能;GDE算法的检测概率较高,检测性能相对稳定,设定Γ(N)=2.3/log(N);ITA算法依靠所有SU感知数据,通过迭代判决实时的获取判决门限,在提升检测性能的同时提高了感知效率,增强了算法对抗噪声功率不确定度的鲁棒性.
|
图 3 GDTO、EGC算法、ITA算法检测概率性能对比 |
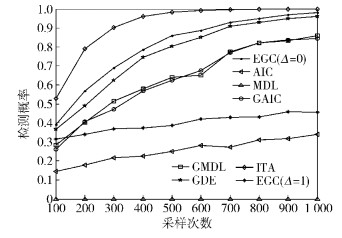
仿真2 在协作CR系统环境中仿真GDTO算法、EGC算法、ITA算法.设定SNR为-12 dB,期望虚警PFA, DES=0.1,在不同采样次数N下的性能比较如图 4所示. ITA算法有效改善了EGC算法的性能,提高了不同采样次数下的性能稳定性. GDTO算法中ITC感知算法经Gerschgorin圆盘算法改进之后性能明显提升,GLE算法感知性能远远大于传统ITC算法;GDE算法充分考虑全局统计量优化感知结果,因而,在不依赖先验信息的条件下检测概率较高且感知性能相对稳定,受到采样检测次数的影响不明显.仿真结果表明,OUS算法的性能明显优于传统SDF感知算法.
|
图 4 GDTO、EGC算法、ITA算法检测概率性能对比 |
提出了基于GDT的最优用户选择协作频谱感知方案,在无须PU信号、信道、噪声功率等精确先验信息的条件下,通过引入GDT,充分利用多个协作用户的感知数据,实现自适应最优用户选择,生成最优GTS.仿真结果表明,该方案仅需较少的协作用户就能获得较高的感知性能,在采样次数较少时可保持相对稳定的感知性能,并且对噪声功率的不确定性具有较强的鲁棒性.因而,基于GDT最优用户选择协作频谱感知方案具有很强的可实现性.
| [1] | Hoyhtya M, Hekkala A, Katz M D. Cognitive wireless networks[M]. Chapter 18, Spectrum Awareness: Techniques and Challenges for Active Spectrum Sensing. Springer Netherlands, 2007. |
| [2] | Quan Zhi, Cui Shuguang, Sayed A H. Optimal linear cooperation for spectrum sensing in cognitive radio networks[J].IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 28–40. doi: 10.1109/JSTSP.2007.914882 |
| [3] | Ma Jun, Zhao Guodong, Li Ye. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks[J].IEEE Transactions on Wireless Communications, 2008, 7(11): 4502–4507. doi: 10.1109/T-WC.2008.070941 |
| [4] |
彭涛, 郭晨, 王文博. 认知无线电网络高能效协作频谱感知技术[J]. 北京邮电大学学报, 2010, 33(4): 93–96.
Peng Tao, Guo Chen, Wang Wenbo. Energy-efficient cooperative spectrum sensing in cognitive radio networks[J].Journal of Beijing University of Posts and Telecommunications, 2010, 33(4): 93–96. |
| [5] | Wu Hsien-Tsai, Yang Jar-Ferr, Chen Fwu-Kuen. Source number estimators using transformed Gerschgorin radii[J].IEEE Transactions on Signal Processing, 1995, 43(6): 1325–1333. doi: 10.1109/78.388844 |
| [6] | Schmidt R. Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 |
| [7] | Wang Rui, Tao Meixia. Blind spectrum sensing by information theoretic criteria for cognitive radios[J].IEEE Transactions on Vehicular Technology, 2010, 59(8): 3806–3817. doi: 10.1109/TVT.2010.2065250 |
| [8] | Wax M, Kailath T. Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(2): 387–392. doi: 10.1109/TASSP.1985.1164557 |