2. 陆军航空兵学院, 北京 101123;
3. 中国人民解放军总后勤部 信息中心, 北京 100036
位置信息是无线传感器网络(WSN)中的一种关键基础信息.在节点部署范围较大、节点密度较小的环境中, 很多定位算法在定位精度或成本上不理想.为此, 提出一种利用智能天线方向性的节点自定位算法.该算法包含两类节点:一是配备智能天线、全向天线和全球定位系统(GPS)的中心节点; 二是配备高频率时钟, 可支持基于到达时间(TOA)测距的网络节点.在定位过程中, 中心节点发送有方向性的定位信号, 网络节点借助定位信号判断自身相对于中心节点的角度, 并结合TOA测距信息, 确定自身位置.通过该方法, 节点以较小的运算量得到较精确的定位结果, 且网络中只有中心节点功能较强, 因此系统总体成本低.分析和仿真结果表明, 该方法能以较小的运算量和较低的成本提供较高的定位精度.
2. Institute of Army Aviation, Beijing 101123, China;
3. Information Center of PLA General Logistics Department, Beijing 100086, China
Under the circumstances that wireless sensor network (WSN) nodes are deployed in a vast region and the node density is low, the existing node location algorithms are not optimum selections. A WSN node self-locating algorithm which utilized the directivity of smart antenna is proposed. There are two types of nodes in the objective network of the means. The first type is central node that equipped with global position system (GPS) unit and smart antenna. The second type is normal node that equipped with high frequency crystal oscillator. Normal node can support time of arrival (TOA) based ranging. With the help of directional locating signal sent by central node, a normal node can estimate the angle and distance between itself and the central node, and determine its position combining the angle and TOA based ranging result. Analysis and experimental results show that the proposed algorithm can provide fine location accuracy with relative low cost and low complexity.
位置信息是无线传感器网络(WSN,wireless sensor network)应用中的一项重要内容,当前已经有很多定位方法的研究.在定位方法中,根据定位对象的不同,主要分为WSN自身定位[1]和目标定位.前者关注于WSN部署后,根据其中某些已知位置的节点(锚节点)来求得其他需要定位的节点(未知节点)的位置.常见算法包括三边测量法[2]、质心算法[3]等. Doherty等[4]提出一种基于六边形区域划分的定位算法,利用具有方向性的信号来估计节点的角度,但定位精度有限.王文杰等[5]提出一种网络节点三维位置估计算法,即锚节点利用阵列天线发射正交导频信号.但该算法需要多个锚节点,系统成本相对较高.
本研究提出一种基于智能天线的节点定位算法,所有网络节点配备成本远低于全球定位系统(GPS,global position system)模块的高频率晶振,能够支持基于到达时间(TOA,time of arrival)的定位.系统中只有一个配备GPS模块与智能天线的中心节点,利用智能天线的波束赋形特性向所有节点发送定位信息,使各节点能够自行求出自身与中心节点的相对角度.再结合TOA的测距结果,求得自身位置.该方法只需1个中心节点,成本大大减少.商用的可装载在手机上的微型智能天线[6]的出现,使得体积足够小巧的中心节点可实现.中心节点与WSN网关为同一设备,不会因定位的需要增加额外成本,相对于系统整体部署成本来讲,中心节点成本是可接受的.在本研究中,中心节点向系统上报自身的经纬度信息以及其他节点与中心节点的相对位置信息,属于绝对定位与相对定位结合的定位,这不仅能减少位置信息传输带来的开销,而且可以通过简单计算来求得节点的绝对位置信息.
1 算法流程在网络部署前,中心节点与所有网络节点均处在一个较小的区域中,此时所有节点激活,接收外部时钟设备发出的同步信号,所有节点实现初始的时间同步.由于定位操作在节点部署后一段时间即可完成,在这段时间内,可认为所有节点通过自身的计时器能实现完全同步.之后的定位操作分为基于TOA测距的距离计算与基于智能天线、借助接收信号强度(RSS,received signal strength indication)测距的角度估计两个部分,算法流程如图 1所示.

|
图 1 节点定位算法流程 |
算法开始时,中心节点通过全向天线广播定位起始信号,监测区域内所有网络节点接收到该信号后,不再进行任何数据传输,等待接收定位信号.之后,中心节点通过智能天线发送定位信号.定位信号通过赋形波束进行传输.赋形波束以中心节点为圆心,以正北方向为起点(该方向对应0°),顺时针旋转,以AS为角度间隔,在每个位置上发送1次定位信号,如图 2所示.之后中心节点通过全向天线广播定位结束信号.定位信号帧结构如图 3所示,其中包含信号发送时间和波束中心方向角度值.由于赋形波束波瓣有一定宽度,节点在接收到节点定位开始和结束信号之间可收到多个定位信号.所有节点通过所收到的定位信号对自身与中心节点的距离与角度进行计算,具体算法下节中详述.

|
图 2 智能天线波束赋形扫描示意图 |

|
图 3 定位信号帧结构 |
设节点i完成距离与角度的计算后,求得与中心节点的距离为Ri,角度为Ai,则可求得自身与中心节点的相对坐标(xi, yi)=(RisinAi, RicosAi),此时该节点i的位置已经确定.
2 算法细节2.1 网络节点与中心节点距离的计算在成熟的TOA测距算法基础上,笔者利用节点接收到的多个定位信号进行多次重复测量.当赋形波束宽度为AW时,节点收到定位信号数为K=「AW/AS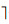
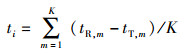
|
(1) |
进而求得自身与中心节点的距离

|
(2) |
其中C为光速.至此可得节点i与中心节点的距离估计结果为Ri.
2.2 网络节点角度的估算无线信号传播的对数常态分布路径损耗模型[7]为
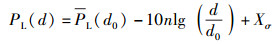
|
(3) |
其中:PL为路径损耗值;n为路径损耗指数,取值在2~6之间;d0为近地参考距离,通过测试获得;Xσ是表示误差的均值为0的高斯随机变量.又有
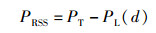
|
(4) |
节点i接收到全向天线发送的节点定位开始和结束信号,提取这2个信号的RSS,在已知这2个信号发送功率PT的情况下,根据式(4) 求得PL(d),则可对自身与中心节点间的距离进行估算
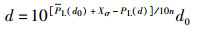
|
(5) |
智能天线的赋形波束主瓣宽度AW取3 dB波瓣宽度的定义,即主瓣的2个边缘处场强为最大场强处的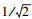
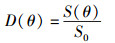
|
(6) |
其中:S0为无方向性天线的功率密度,S(θ)为智能天线在角度θ上的功率密度.可知PTk=S(θk),代入式(6) 可得对应的方向性系数D(θk),进而求得角度值θk.虽然智能天线方向性轴对称,但由于已知节点i的角度Ai在AT1和AT2之间,因此有
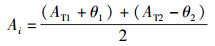
|
(7) |
Ai为网络节点i相对于中心节点的角度估算结果.以上步骤重复迭代数次,进行平均后得到准确度更高的数值.
3 仿真与讨论考虑边长L=2 000 m的正方形监控区域.所有网络节点都有全向天线,能测量接收信号的RSS,最大通信距离为rmax=50 m[8].网络节点配备高精度时钟,时钟频率f0=1 016 MHz.节点在监控区域内均匀分布,节点数N=1 500.设中心节点自身位置坐标为(0, 0),配备智能天线和全向天线,最大通信距离为Rmax=1 400 m[6].
中心节点智能天线赋形波束的波束宽度AW=15°[6],旋转步长AS=10°,当噪声方差为10 dBm时,随着网络节点与中心节点的距离增加,角度估计误差及相应的距离估计误差有所增加,如图 4所示,这是因为角度估计中利用了基于RSS的测距,随着距离的增加,信号强度受干扰的影响增加.虽然提出的算法中RSS测距对角度估计的影响能够部分抵消,但还是出现了一定的误差.

|
图 4 所提算法角度估计误差及相应的距离估计误差 |
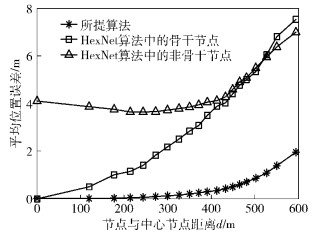
图 5所示为随着与中心节点距离的不同,采用所提算法与HexNet算法[4]得到的网络节点定位误差的比较(节点估计位置与实际位置的距离).可以看出,当网络节点与中心节点距离较近时,HexNet算法中的骨干节点定位精度与所提算法接近,而随着网络节点与中心节点距离的增加,两者差距变大.这是由于所提算法中,基于智能天线的角度估计是结合了2个信号的RSS进行处理,抵消了部分噪声的影响.
|
图 5 与HexNet算法的定位误差比较 |
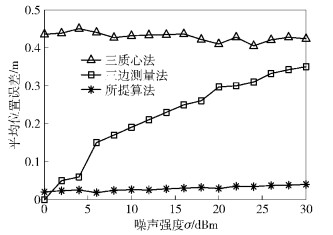
在路径损耗指数为4时,随着噪声强度的增加,所提的算法的平均定位精度(所有节点的估计位置与实际位置的距离的平均值)与三边测量法、质心算法的平均定位精度的比较如图 6所示.通过比较可知,三边测量法的定位误差随着噪声强度的增加而增加,质心算法和所提算法的误差较稳定,主要原因是前者模型的性能会随着节点布局而发生改变,受噪声和路径损耗的影响不大,而后者定位中的TOA测距基本不受噪声的影响,且后者的精度高于前者.同时,所提算法中只需一个配备GPS的中心节点,与需要多个锚节点的其他算法相比,成本较低.
|
图 6 所提算法与经典定位算法平均定位精度比较 |
提出一种节点自定位算法,利用智能天线的方向性,并结合了基于TOA、RSS测距的定位方法的优点.理论分析和仿真结果表明,该方法能实现较高的定位精度,同时成本较小.
| [1] |
王福豹, 史龙, 任丰原. 无线传感器网络中的自身定位系统和算法[J]. 软件学报, 2005, 16(5): 854–868.
Wang Fubao, Shi Long, Ren Fengyuan. Self-localization systems and algorithms for wireless sensor networks[J].Journal of Software, 2005, 16(5): 854–868. |
| [2] | Gentile G. Distributed sensor location through linear programming with triangle inequality constraints[J].IEEE Trans on Wireless Communications, 2007, 6(7): 2572–2581. doi: 10.1109/TWC.2007.05907 |
| [3] | Doherty L, Pister K S J, Ghaoui L E. Convex position estimation in wireless sensor networks[C]//IEEE INFOCOM 2001. Anchorage: IEEE Computer and Communications Societies, 2001(3): 1655-1663. |
| [4] | Hady S. AbdelSalam, Stephan Olariu. Hexnet: hexagon-based localization technique for wireless sensor networks[C]//2009. IEEE International Conference on Pervasive Computing and Communications. Galveston, Texas: IEEE Computer and Communications Societies, 2009(1): 1-6. |
| [5] |
王文杰, 张渭乐, 殷勤业. 利用离去角度的无线传感器网络分布式节点定位方法[J]. 西安交通大学学报, 2010, 44(2): 61–68.
Wang Wenjie, Zhang Weile, Yin Jianye. A distributive localization method for wireless sensor networks using angle departure[J].Jornal of Xi'an Jiaotong University, 2010, 44(2): 61–68. doi: 10.7652/xjtuxb201002013 |
| [6] | Sofant Technologies. World's smallest smart antenna to revolutionise smart phone performance[EB/OL]. 2013. http: //www. sofant. com/PR2012100301. php. |
| [7] | Ramakrishna Janaswamy. Radiowave propagation and smart antennas for wireless communications[M]. Netherlands: Kluwer Academic Publishers, 2002. |
| [8] | Moog Inc. Mica2 datasheet 6020-0042-07 rev a[EB/OL]. 2013. http://www.xbow.com. |


