针对分布式无线网络中用户关系拓扑结构的任意性和复杂性带来的维灾问题, 提出了一种基于图型博弈的动态频谱接入算法.利用环境信息的非对称性把频谱接入问题抽象为图型博弈模型, 并用模型中的图型拓扑表示现实环境中博弈的内在结构; 以最小化个人后悔值代替最小化系统后悔值来求解纯策略纳什均衡点.与现有算法比较, 该算法能有效降低运算复杂度, 满足通信中实时性的要求.仿真结果表明, 该算法能快速收敛到无冲突的纯策略纳什均衡, 提高了系统容量和功率利用率, 在资源匮乏时优势明显.
To solve the dimension disaster problem from the arbitrariness and complexity of user-relationship topology in distributed wireless network, a dynamic spectrum access algorithm is presented based on graphical game. Relying on information asymmetry environment, the users accessing channel is modeled as a graphical game so as to construct a new internal game in realistic environment. Pure-strategy Nash equilibrium without conflict is obtained by minimizing the regret value of person instead of that of system. Compared to the existing literatures, the algorithm can reduce the computing complexity effectively and meet the real-time communication requirements. Simulation results show that the pure-strategy Nash equilibrium achieves better system performance in terms of capacity and power utilization, specifically in the system with scare resources.
分布式无线网络中,用户的接入行为不仅会影响环境的变化,而且还会影响其他用户的行为和效用[1],运用博弈论可以有效地分析用户的这一行为特点[2].然而采用传统的博弈模型来求解竞争频谱接入,往往是一个NP-complete或NP-hard问题[3].为了在复杂环境中更有效地分配有限的资源,无悔学习[4]和次梯度算法[5]被用来优化系统的解.近年来,在认知无线电网络中图型博弈理论被提出研究竞争用户之间的频谱感知协作学习[6],基于拍卖博弈的频谱共享机制[7].干扰图型博弈模型[8],最大化区域群落效用模型[9]等被用来分析和提升系统效用.
针对分布式无线网络中用户信息的非对称性,将用户真实的博弈结构采用图型博弈构架表示;然后提出了一种新的接入算法.该算法通过交换协作社区用户的行为信息和后悔值信息以及运用严格潜在博弈性质最小化个体后悔值代替最小化系统后悔值来求解纯策略纳什均衡;最后,实现了分布式网络中动态资源的有效接入.该算法能保证用户收敛到一个无冲突的纯策略纳什均衡,提升了系统容量和功率利用率.
1 系统模型1.1 基于用户关系的图型博弈构架通常针对分布式无线网络的策略形成机制都是基于所有参与学习的用户都相互影响,但这种假设并不总适宜.用户的地理位置、对资源的使用权限、社会环境中的角色和关系、信息的获取能力等因素决定了环境信息存在非对称性,这使得用户的行为具有局部性.为此,将用户实际环境下的博弈结构抽象为简约的图型博弈模型.图型博弈只需针对博弈图中有博弈关系的用户,避免为所有网络用户构建博弈元素,用户的关系网络也从网状网变成了稀疏网,降低了博弈的维数和复杂度.
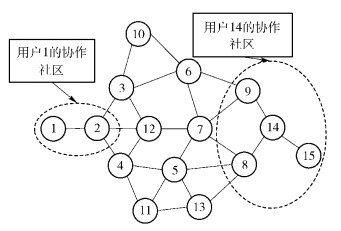
用图论中的无向图来表示节点间相互的直接竞争关系(或干扰关系),如图 1所示.假设用户集合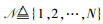
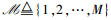
|
图 1 协作社区 |
定义1 协作社区:用户i与其有直接竞争关系的所有用户构成一个协作社区Ji,即
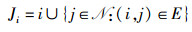
|
(1) |
J-i表示社区中除去用户i的其他用户的集合. Ai表示用户i所有可能的行为集合,即所有可观测的信道. Ai(k)表示用户i在第k次迭代时的可用行为集,ai(k)表示用户i在第k次迭代时的行为.用户能观察到自己社区内其他用户的行为.对于任意的用户Ai(k)={Ai-aj(k)}. u(ai(k), a-i(k))表示用户i在第k次迭代时的效用.
如果用户l∉Ji,那么其行为策略不会对用户i产生直接的影响.所以u(ai, a-i)=u(ai, aJ-i).这样可以去除不相干的用户,降低系统复杂度.
假设:1) 信道m对用户i的效率为Rimbit,Rim∈[0,1]随机分布. 2) 用户能感知所有信道并选其一传输,不同用户对同一信道的感知结果可不同. 3) 用户i的效用函数:ui(ai, aJ-i)=Rimδ(i, j).其中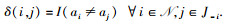
定义2 系统容量:分布式无线网络中,所有用户的效用之和,即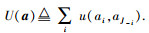
图型博弈下纯策略纳什均衡的降维表达式为

|
(2) |
定理1 提出的图型博弈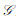
证明 设潜在函数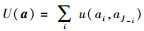
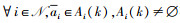
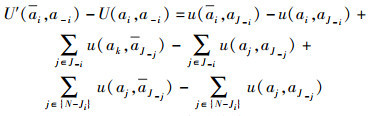
|
(3) |
因为i与j, j∈ 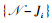
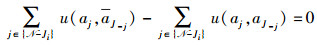
|
(4) |
因为Ai(k)≠∅,ai≠aj, ∀j, j∈J-i,所以
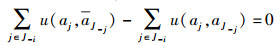
|
(5) |
由式(3)~(5) 得

|
(6) |
由式(6) 得出此博弈是一个严格潜在博弈,至少存在一个纯策略纳什均衡.证毕.
定义3 最优策略:策略aopt=(a1opt, a2opt, …, aNopt)能使系统效用达到最大值,即
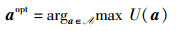
|
其中
定理2 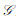
证明 设aopt=(a1opt, a2opt, …, aNopt)是最优策略,则U(aopt)≥U(a), ∀a, a∈ 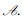
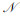
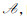
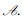
定理2说明了系统最优解与个人最优解并不矛盾.求解图型博弈的纳什均衡可获得最佳资源接入.
在周期k,若ai∈Ai(k), 当前环境下的最佳反应为ai=arg max u(ai, aJ-i), ai∈Ai(k),那么用户的个人后悔值为Gi(ai)=u(ai, aJ-i)-u(ai, aJ-i).
由于此博弈是一个严格潜在博弈,用户后悔值的减小同样也会使得系统后悔值减小.因此,最终目标是最小化用户后悔值,而不是最优化系统后悔值,即
当资源数M小于用户关系网中最大网状网的用户个数q时,接入均衡只有带冲突的纳什均衡.因为如果用户关系网络形成一个网状网,那么任意两个用户获得的资源必须不同.所以达到纳什均衡即可退出循环.当M≥q时,用户的接入均衡有带冲突的纯策略纳什均衡和无冲突的纯策略纳什均衡,获得无冲突纯策略纳什均衡的算法步骤如下.
1) 用户采用贪婪算法初始化信道选择:ai=arg maxu(ai), ai∈Ai.
2) 用户i计算后悔值,并将其与任意用户j(j∈J-i)的后悔值进行比较.
3) 若Gi(ai(k)) > Gj(aj(k)),则ai(k+1)=ai(k),aj(k+1)=aj(k);若Gi(ai)=Gj(aj),用户i、j以等概率接入ai(k), aj(k);否则,ai(k+1)=ai(k).
4) 对于∀i,当M≥q时,如果Gi=0且ui=0,用户i随机选择ai∈Ai.进入步骤2);Gi=0且ui≠0,退出迭代;Gi≠0,进入步骤2).
当M < q时,如果Gi=0,退出迭代;否则,进入步骤2).
值得说明的是,Gi=0且ui=0表示用户i进入带冲突的纳什均衡,即获得了局部最优解.用户i通过随机选择来打破原本的局部最优.
定理3 按照提出的新算法进行信道选择,在M≥q时,必收敛到一个无冲突的纯策略纳什均衡.
证明 在M≥q时,设第k次迭代中,对于∀i有Gi≠0或ui≠0.
若Gi=0,ui≠0,ui(ai, aJ-i)≥ui(ai, aJ-i)由纳什均衡定义有用户达到均衡,且无冲突.
若Gi≠0,设∃i, ∃j, i, j∈Ji,Gi(a′i(k))≠0,a′i(k)∈Ai(k)={Ai-aj(k)},Gj(a′j(k))≠0,a′j(k)∈Aj(k)={Aj-ai(k)},设Gi(a′i(k)) > Gj(a′j(k)).那么ai(k+1)=a′i(k),aj(k+1)=aj(k).
因为在同一个社区只有一个用户调整信道,则
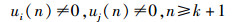
|
(7) |
因为aJ-i(k+1)=aJ-i(k),由Gi(a′i(k+1))=0,则

|
(8) |
若Gj(a′j(k+1))=0,有
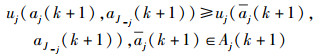
|
(9) |
由式(7)~(9) 用户i、j达到无冲突的纳什均衡.
若Gj(a′j(k+1))≠0,则Gj(a′j(k+1))大于Gi(a′i(k+1)),有aj(k+2)=a′j(k+1)≠aj(k),ai(k+2)=ai(k+1),aJ-j(k+2)=aJ-j(k+1) 那么
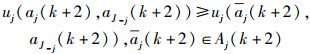
|
(10) |
若Gi(a′i(k+2))=0,那么
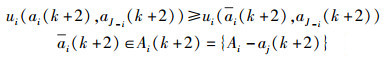
|
(11) |
由式(7)(9)~(11) 知用户i、j达到无冲突均衡.
若Gi(a′i(k+2))≠0,必有
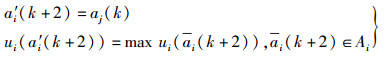
|
(12) |
其中Ai(k)∪Ai(k+2)=Ai.
令ai(k+3)=a′i(k+2), aj(k+3)=aj(k+2),则
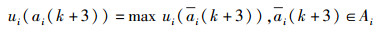
|
(13) |
由式(7) 和式(13) 可知,用户i的效用达到最大值,以后的迭代将不会改变行为.用户j也会在下一次的迭代中达到最大值,用户i, j达到无冲突的纯策略纳什均衡.多用户同理可证.证毕.
3 算法比较与仿真分析3.1 算法复杂度比较用穷举法指示性能上界.如表 1所示,将新算法与穷举法、次梯度算法和SAP(spatial adaptive play)算法在运算量方面进行比较,N为用户数,M为信道数,d为用户的度.
|
|
表 1 运算量比较 |
在大规模分布式无线网络中,用户的竞争关系拓扑图具有任意性,不失一般性,随机生成如图 1所示的竞争关系拓扑结构.假设每个用户的固定发射功率为65 mW,传输速率Rim∈[0,1]bit随机分布.
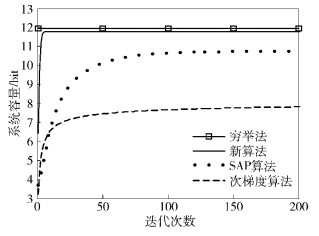
图 2显示了提出的算法与次梯度算法、SAP算法在信道数为5时平均系统容量收敛速度方面的比较结果.很明显,提出的算法能快速收敛到纳什均衡并逼近穷举法的计算结果.其他2种算法经过多次迭代后仍处于较低水平.由于穷举法与其他算法相比所需的计算量太大,下列仿真结果中均只给出了穷举法的最终结果作为性能界.
|
图 2 各算法迭代次数与平均系统容量的关系 |
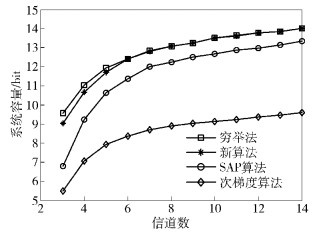
图 3显示了随着信道数的增加系统容量都有所增加.当信道数较为充裕时,提出的算法十分接近穷举法的平均系统容量.在信道匮乏时,提出的算法的平均系统容量明显高于SAP算法和次梯度算法.随着无线通信业务快速发展、频谱资源更加稀缺,提出的算法可以更好地体现其优势与实际意义.
|
图 3 各算法均衡后的平均系统容量 |
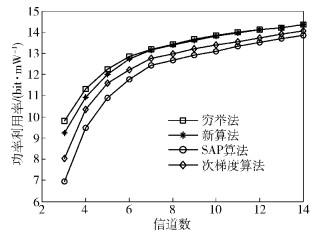
图 4表明,提出的算法的功率利用率高于另两种算法,略低于穷举法.在信道相对充裕的情况下,该算法略高于其他两种;但在信道较少时,该算法的功率利用率最高可以高出次梯度算法12%,最高可以高出SAP算法28%.
|
图 4 各算法均衡后的平均功率利用率 |
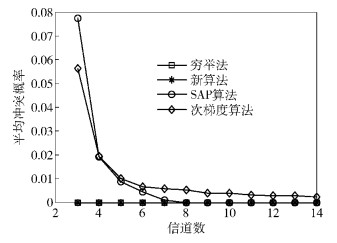
如图 5所示,随着信道数的增多,达到均衡后的系统平均冲突率不断减小.提出的算法可以真正实现无冲突的资源接入. SAP算法在信道较少时也可以收敛到无冲突的纳什均衡,但是以一定的概率收敛到无冲突的纳什均衡点上,从平均冲突率来说其也不能实现无冲突的信道接入.次梯度算法求取混合均衡,不易收敛到纯策略纳什均衡.
|
图 5 各算法均衡后系统的平均冲突率 |
利用环境信息的非对称性,把问题简化为简约的图型博弈模型,将关系拓扑由传统的网状网结构转化为稀疏网络结构,进行了有效的降维;证明了提出的图型博弈存在纯策略纳什均衡,且系统的最优策略就是一个纯策略纳什均衡.根据博弈是严格潜在博弈,提出了一种新的频谱接入算法,以最小化个人后悔值代替系统后悔值,证明了该算法必然收敛到无冲突的纯策略纳什均衡.提出的算法在信道资源较少的情况下,其系统容量、能量效率、冲突率3种性能均得到提升.
| [1] | Nie N, Comaniciu C. Adaptive channel allocation spectrum etiquette for cognitive radio networks[C]//DySPAN 2005. Baltimore: IEEE, 2005: 269-278. |
| [2] | Ni Qiang, Zarakovitis C C. Nash bargaining game theoretic scheduling for joint channel and power allocation in cognitive radio systems[J].IEEE Journal on Selected Areas in Communications, 2012, 30(1): 70–81. doi: 10.1109/JSAC.2012.120107 |
| [3] | Zhu Han, Niyato D, Saad W, et al. Game theory in wireless and communication networks theory, models, and application[M]. New York: Cambridge University Press, 2012: 205-392. |
| [4] | Zhu Han, Pandana C, Liu K J R. Distributive opportunistic spectrum access for cognitive radio using correlated equilibrium and no-regret learning[C]//WCNC'07. Kowloon: IEEE, 2007: 11-15. |
| [5] | Nedic A, Ozdaglar A. Distributed subgradient methods for multi-agent optimization[J].IEEE Transactions on Automatic Control, 2009, 54(1): 48–61. doi: 10.1109/TAC.2008.2009515 |
| [6] | Clutton-Brock T. Cooperation between non-kin in animal societies[J].Nature, 2009, 462(7269): 51–57. doi: 10.1038/nature08366 |
| [7] | Azarafrooz M, Chandramouli R. Distributed learning in secondary spectrum sharing graphical game[C]//GLOBECOM 2011. Houston: IEEE, 2011: 1-5. |
| [8] | Li Husheng, Zhu Han. Competitive spectrum access in cognitive radio networks: graphical game and learning[C]//WCNC 2010. Sydney: IEEE, 2010: 1-6. |
| [9] | Wu Yuhua, Wang Jinglong, Wu Qihui, et al. Social welfare maximization for SRSNs using bio-inspired community cooperation mechanism[J].Chinese Science Bulletin, 2012, 57(1): 125–131. doi: 10.1007/s11434-011-4775-6 |



