为了合理规划建设经济可靠的电力通信网络, 提出了一种基于免疫算法的电力通信网线路规划方法, 综合考虑了网络的经济性、可靠性和业务分布因素.基于站点成环率构造出网络可靠性函数, 结合业务分布情况设计了电力通信网线路规划的问题模型, 并利用免疫算法进行求解.该方法采用多目标优化模型, 能在一定程度上提高规划方案的灵活性和全面性.仿真结果表明, 在面对不同站点成环率约束的情况下, 该方法均能提供有效的线路规划方案.
In order to construct a most reliable power communication network within minimal construction cost, a path planning method based on immune algorithm is presented, which takes into account economy, reliability and service distribution. In the method, the network reliability function is designed based on cyclization rate, and the path planning model is built by the factors of service distribution. This method will increase the flexibility and completeness of planning result. Simulation results show that the proposed method is capable of providing efficient results under diverse cyclization rate constraint.
电力通信网是保证电力系统安全稳定运行的基础[1].近年来,随着智能电网的高速发展,电力通信网的规模也随之大幅提升.由于电力通信高可靠性的要求,在通信线路规划建设阶段不能仅考虑经济性指标,也要考虑到电力通信网的可靠性和业务分布[2].因此,研究均衡电力通信网络的经济性、可靠性和业务分布,以最小的代价建设最可靠的电力通信网成为电力通信网规划的关键问题之一.
目前针对电力通信网规划问题已有一些研究,Wang等[3]抽象出通信线路的经济性模型,有效地减小了通信线路的建设成本. Jahromi与Su等[4-5]与Wang的研究思路相近,然而其均没有考虑可靠性约束,导致网络在出现故障时,受影响的业务无法及时恢复. Habib等[6]通过向网络中添加通信站点造成资源冗余,提高网络可靠性,然而增加冗余站点会大大提高网络的建设成本,不仅无法保证网络建设的经济性,还会造成不必要的资源浪费.
针对电力通信网规划中存在的问题,笔者综合考虑了线路建设的经济性、可靠性和业务分布等因素,重点解决电力通信网规划中的光传输网线路规划问题.首先,基于图的结构抽象出电力光传输网络模型,引入网络建设成本函数,并基于站点成环率这一电力通信网的重要特性构建出可靠性约束,从而建立光传输网线路规划的数学模型,并利用免疫算法对问题进行求解.仿真结果表明,所提算法在收敛时间和稳定性方面都表现较优.
1 电力光传输网线路规划问题模型电力光传输网线路规划是指在进行网络扩建时,已知业务分布情况和通信站位置的基础上,根据现有的网络结构和待选光缆线路,在满足各种可靠性和业务分布约束的前提下,确定出经济性最佳的光缆布线方案.以图的结构对问题进行建模,图的顶点表示通信站点,边表示光缆线路,该问题就是如何从图中m条待选线路中选择k(k≤m)条线路构成最经济可靠的网络结构.
为了抽象出电力光传输网线路规划问题的数学模型,首先要引入网络建设成本函数、可靠性约束和业务分布约束.
1) 网络建设成本函数:在规划方案中新加入网络光缆线路的建设成本,即
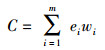
|
(1) |
其中:C为网络建设成本;m为待选光缆线路数;ei为0-1变量,即

|
(2) |
wi为第i条线路ei的建设成本.
2) 网络可靠性约束:电力光传输网中以站点成环率来体现网络可靠性,其值为网络中成环站点数和总站点数的比值,即
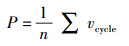
|
(3) |
其中:P为站点成环率;n为网络中站点的总数;vcycle为成环站点,成环站点是指在网络中由光缆相连而构成回路的站点,其与拓扑结构紧密相关,而与节点和链路自身的可靠性无关.
3) 业务分布约束:假设已知在规划期间内,站点u和站点v之间存在大量业务,要求其时延和路由跳数尽可能小,因此在进行线路规划时应考虑在u和v之间建设一条直连光缆,即边e(u,v)存在.
综上所述,得到电力光传输网线路规划的数学模型为
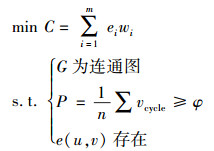
|
(4) |
约束中第1部分保证规划后的网络拓扑是一个连通图,不允许出现网络解裂的情况;第2部分中的φ是一个阈值,可以手动调整来设置站点成环率约束;第3部分是业务分布约束.
2 基于免疫算法的线路规划机制2.1 算法完整架构由式(4) 可以看出,电力光传输网线路规划属于多目标优化问题,其已被证明是NP难问题[5],智能优化算法可以在有限时间内求解此类问题.在众多智能优化算法中,免疫算法在收敛时间和稳定性上表现较优[7],且免疫算法中的“疫苗”可以用线路规划问题中的业务分布来体现,故选取免疫算法对问题模型进行求解.
算法的完整步骤如下.
步骤1 系统初始化,导入待规划的电力光纤通信网数据,设置算法参数,生成nR个抗体作为初始种群R(t),注射全局疫苗,设置进化迭代数t=0.
步骤2 计算每个抗体的亲和度,并按亲和度对R(t)中的抗体进行降序排列,并提取局部疫苗.选择R(t)中前ns个抗体构成克隆父代种群S(t).
步骤3 对S(t)进行克隆操作生成种群T(t).
步骤4 对种群T(t)中的每个抗体进行变异操作,变异后的抗体按比例接种局部疫苗,生成种群T′(t).
步骤5 计算种群R(t)∪T′(t)中每个抗体的亲和度和浓度.
步骤6 计算R(t)∪T′(t)中每个抗体的选择概率Pchoice,并按此概率进行选择,生成种群R(t+1).
步骤7 若t > tmax,则输出R(t);否则,令t=t+1,转至步骤2.
2.2 算子设计1) 抗体亲和度函数:由经济性和可靠性两方面决定.其中,经济性用式(1) 中的目标函数C表示,可靠性用式(3) 中的成环率P表示.抗体Sv的亲和度函数为
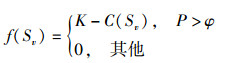
|
(5) |
其中K为一个大数,保证f(Sv)的值为正.
2) 抗体浓度:设f(Sv)和f(Sw)分别为抗体Sv和抗体Sw的亲和度,则
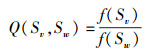
|
(6) |
为代表抗体Sv和抗体Sw的相似度指标.若存在任意正数ε,使
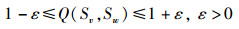
|
(7) |
成立,则称抗体Sv和抗体Sw相似,记为
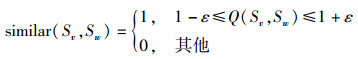
|
(8) |
抗体Sv的浓度是指种群中与Sv相似的抗体的数目与种群规模的比值,记为

|
(9) |
其中Ns为种群规模.
3) 克隆算子:对抗体Sv进行克隆,生成m个副本,构成Sv的子代集合tSet(Sv),即
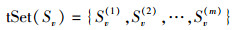
|
(10) |
对父代种群S={s1, s2, …, sn}进行等比例克隆,即每个抗体生成m个副本,形成新的种群T:
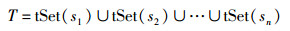
|
(11) |
种群T的规模与初始种群规模相同.
4) 选择算子:在选择抗体时,既要保证优秀抗体能以较大的概率被选中,又要保证子代种群的多样性,因此采用正比抗体亲和度、反比抗体浓度的选择算子,即

|
(12) |
其中Pc(Sv)为抗体Sv的选择概率.
3 实验分析3.1 仿真环境为了验证所提出的免疫算法对电力光传输网线路规划的有效性,将利用该算法对18节点系统进行仿真实验. 18节点系统是电力系统中常见的一个仿真网络[8],其结构如图 1所示,其中实线表示原有线路,虚线表示待扩建线路.

|
图 1 18节点系统结构图 |
该算法中,克隆父代种群取30,变异概率取0.1,种群规模均取100,最大进化代数取500,进行以下2组实验.
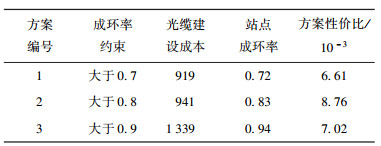
实验1 算法以规划方案的经济性最优为优化方向,调整站点成环率P的阈值φ,形成3种不同规划方案:方案1的P大于0.7、方案2的P大于0.8、方案3的P大于0.9.
实验2 加入业务分布约束.算法以规划方案的经济性最优为优化方向,要求P大于0.5,分别假设在站点9和站点16(方案4)、站点4和站点7(方案5) 之间存在大量继电保护业务,要求其间必须有光缆直连.
3.2 结果分析实验1中3种成环率约束下的抗体亲和度随进化代数的变化如图 2所示.
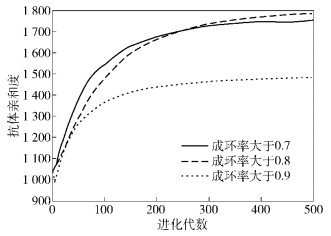
|
图 2 不同成环率下抗体亲和度变化 |
由图 2可以看出,在面对不同的站点成环率约束时,算法的抗体亲和度在进化初期快速上升,并均能在有限进化代数内达到收敛,说明该算法能提供基于不同成环率约束的电力光传输网线路规划方案.
3种成环率约束下的实验结果如表 1所示.
|
|
表 1 3种成环率约束下的实验结果 |
由表 1可以看出,3种规划方案的成环率分别为0.72、0.83和0.94,均满足约束条件;同时,光缆建设成本随成环率的提高而增加,这是因为需要建设更多的光缆使站点连接成环.
实验2中方案4假设在站点9和站点16之间存在大量继电保护业务,要求其间必须有光缆直连;方案5假设在站点4和站点7之间存在大量继电保护业务,要求其间必须有光缆直连.这2种规划方案的结果如表 2所示.
|
|
表 2 不同业务分布的实验结果 |
由表 2可以看出,方案4和方案5的站点成环率分别为0.72和0.56,均满足成环率大于0.5的要求.以方案4为例,其网络结构如图 3所示,可见在站点9和站点16之间有光缆线路直连,满足业务分布约束.
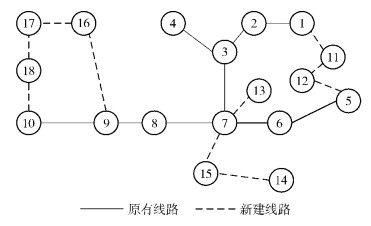
|
图 3 方案4网络结构 |
为了均衡和保证电力光传输网线路建设的可靠性和经济性,提出了基于免疫算法的电力光传输网线路规划方案.在以经济性最优的基础上,加入了成环率和业务分布约束,实验结果表明,所提算法在面对不同成环率取值时均能提供有效的线路规划方案,且能很好地兼顾业务分布因素,具有很高的灵活性,实验的仿真环境是一种简化的理想状态,下一步将结合更贴近实际的数据,增强说服力.
| [1] | Ye Yan, Yi Qian, Hamid S, et al. A survey on smart grid communication infrastructure: motivations, requirements and challenges[J].IEEE Communications Surveys and Tutorials, 2013, 15(1): 5–20. doi: 10.1109/SURV.2012.021312.00034 |
| [2] |
吴小辰. 南方电网"十二五"电力通信发展规划综述[J]. 电力系统通信, 2011, 32(5): 7–9.
Wu Xiaochen. Review of power communication development plan of China southern power grid in the twelfth five-year plan period[J].Telecommunications For Electric Power System, 2011, 32(5): 7–9. |
| [3] | Wang David Tse-chi, Ochoa L F, Harrison G P. Modified GA and data envelopment analysis for multistage distribution network expansion planning under uncertainty[J].IEEE Transcations on Power Systems, 2011, 26(2): 897–904. doi: 10.1109/TPWRS.2010.2057457 |
| [4] | Jahromi A E, Rad Z B. Optimal topological design of power communication networks using genetic algorithm[J].Scientia Iranica, Transactions Engineering, 2013, 20(3): 1–13. |
| [5] | Su Haifeng, Zhang Jianhua, Liang Zhirui, et al. Power distribution network planning optimization based on life cycle cost[C]//2010 China International Conference on Electricity Distribution(CICED). Nanjing: [s.n.], 2010: 1-8. |
| [6] | Habib M F, Tornatore M, Dikbiyik F, et al. Disaster survivability in optical communication networks[J].Computer Communications, 2013, 36(6): 630–644. doi: 10.1016/j.comcom.2013.01.004 |
| [7] |
朱思峰, 刘芳, 柴争义. 基于免疫计算的TD-SCDMA网络基站选址优化[J]. 通信学报, 2011, 32(1): 106–110, 120.
Zhu Sifeng, Liu Fang, Chai Zhengyi. Immune computing-based base station location planning in the TD-SCDMA network[J].Journal on Communications, 2011, 32(1): 106–110, 120. |
| [8] | 唐铁英. 人工免疫算法及其在电力系统规划中的应用研究[D]. 杭州: 浙江大学, 2007. |