2. 北京电子科技学院, 北京 100070;
3. 中国科学院 信息工程研究所, 北京 100093
为了研究XOR消息认证码(XOR-MAC)的结构, 从泛Hash函数和伪随机函数的视角, 使用共享随机函数模型对其进行了分析.将XOR-MAC拆分为伪随机函数和泛Hash函数两部分, 然后证明这两部分满足一定的性质, 最后将其看成是一种将伪随机函数应用到泛Hash函数上的Carter-Wegman类型的消息认证码, 并基于信息论给出了简洁的XOR-MAC安全性证明.借助这一思想可以非常容易地设计新的消息认证码.
2. Beijing Electronic Science and Technology Institute, Beijing 100070, China;
3. Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
In order to study the construction of XOR message authentication code (XOR-MAC), we analyse it from the view of universal Hash and pseudo-random function, using shared random funciton model. Firstly, XOR-MAC is splited into two parts: a pseudo-random funtion and an universal Hash. Secondly, this two parts can be proved to have certain properties. Finally, XOR-MAC is regarded as a kind of Carter-Wegman MAC by adopting a new method that applies a pseudo-random functions directly to the output of an universal Hash family. And we give a simple security proof of XOR-MAC based on information theory. The most important thing is that many new MACs can be easily constructed using this idea.
作为信息安全的核心目标之一,信息的完整性在整个信息安全体系中占据着关键位置.消息认证码(MAC, message authentication code)是保证信息完整性最重要的密码学算法,该算法能提供这样的机制:使得消息的接收者可以验证该消息确实来自所声称的消息源,且在传输的过程中未受到未授权的修改.在很多实际应用的例子中,例如金融行业中的转账汇款业务,用户转账汇款的金额往往并不需要保密,真正需要确保的是转账的数额确实是用户想要的金额,而不会被未经授权的他人篡改成别的数额.这时对消息完整性的要求要远远超过对消息保密性的要求.
1 MAC的设计MAC有3种设计思路:第1种是基于带密钥的Hash函数的,如HMAC[1],目前是安全套接层、网络层安全协议等中的完整性算法标准;第2种是基于分组密码的,如XOR-MAC[2]、CBC-MAC[3-4];第3种是基于泛Hash函数的Carter-Wegman MAC [5].通常人们都认为3种设计方法相互独立,没有交集.笔者对常用的基于分组密码构造的XOR-MAC进行了结构分析,将XOR-MAC算法的主体部分定义成泛Hash函数,并证明其是ε-AXU的泛Hash函数,从而可将其整体结构看成是基于泛Hash函数的Carter-Wegman MAC,因而只需证明所有输入到伪随机函数(PRF, pseudo-random functions)中的碰撞是可忽略的,即可获得XOR-MAC的安全性证明,大大简化了之前的各种烦琐复杂的证明[2, 6].最重要的是,这种分析还使得其结构更便于理解,方便设计出新的MAC.
2 XOR-MAC的定义XOR-MAC是Bellare等在文献[2]中提出的,包括2种模式:一种称为XMACR;另一种称为XMACC.其区别仅在于状态值的选择上,XOR-MACR采用的是随机选择状态值,算法定义如下.
XMACRK(M)
pad(M)
if |M| > (n-b-1)2b then return ⊥
Partition M into M[1]…M[m]
R 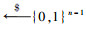
Y[0]=EK(0‖R)
for i←1 to m
Y[i]←EK(1‖Ntostr(i, b)‖M[i])
∑←Y[0]⊕Y[1]⊕…⊕Y[m]
Tag←∑
return Tag
E:K×{0, 1}n→{0, 1}n表示算法所使用的分组密码,Ntostr(i, b)表示将整数i转化成长度为b的二进制表示. M表示消息,|M|表示消息的长度. pad(M)表示将消息M填充为n-b-1的整数倍(填充方式为在消息最后添加1,然后补上若干个0),这样消息M就被分成m个分组,M=M[1]…M[m],其中|M[i]|=n-b-1,i=1, 2, …, m.这里假定m < 2b,也就是说|M| < (n-b-1)×2b.符号⊥表示非法标记.XOR-MACC采用计数器的方式确定状态值,算法定义如下.
XMACCK(M)
pad(M)
if |M| > (n-b-1)2b then return ⊥
Partition M into M[1]…M[m]
C←C+1
Y[0]=EK(0‖Ntostr(C, n-1))
for i←1 to m
Y[i]←EK(1‖Ntostr(i, b)‖M[i])
∑←Y[0]⊕Y[1]⊕…⊕Y[m]
Tag←∑
return Tag
3 Carter-Wegman MACCarter-Wegman MAC是指这样一种体制,首先使用泛Hash函数将要处理的消息压缩成很短的串,然后再使用密码学算法对生成的串进行处理以生成认证标记.
3.1 泛Hash函数族泛Hash函数族是1979年由Carter和Wegman提出的,它广泛应用于计算机科学的各个领域,包括密码学、复杂性理论、编译器以及数据库.泛Hash函数族有很多不同的变体,下面介绍一些要用到的变体.
定义1[7] 设Hash函数h的定义域为D,值域为R,D和R都是有限的二进制串的集合,并且值域R要小于定义域D.如果对于每个x, y∈D,其中x≠y,Prh∈H[h(x)=h(y)]=1/|R|,那么称一个有限的Hash函数集合H={h:D→R}是泛的.
如果放松对碰撞概率的要求,只要求碰撞的概率≤ε,而ε≥1/|R|,就能得到几乎泛的Hash函数族的定义.
定义2[8] 设ε∈R+是一个正数,Hash函数h的定义域为D,值域为R,D和R都是有限的二进制串的集合,并且值域R要小于定义域D.如果对于任意x, y∈D,其中x≠y,Prh∈H[h(x)=h(y)]≤ε,那么称一个有限的Hash函数集合H={h:D→R}是几乎ε泛的(记为ε-AU).
定义3 设ε∈R+是一个正数,Hash函数h的定义域为D,值域为R,D和R都是有限的二进制串的集合,并且值域R要小于定义域D.如果对于任意x, y∈D,其中x≠y,任意c∈R,有Prh∈H[h(x)⊕h(y)=c]≤ε,那么称一个有限的Hash函数集合H={h:D→R}是几乎ε-XOR泛的(记为ε-AXU).
3.2 由泛Hash函数构造MACCarter-Wegman最初的构造是基于共享随机函数模型的.首先假定有一个ε-AXU的Hash函数族H={h:D→{0, 1}n},同时有一个无限随机比特串P=P1P2…,其中|Pi|=n.随机地选择一个h∈H,在发送者和接收者之间共享的密钥是(h, P),发送者有一个计数器cnt,它是一个整型变量,初始值为0,每发送1个消息增加1.假设发送者要发送第cnt个消息M给接收者,它发送如下三元组(M, cnt, Pcnt⊕h(M)).接收者在接到消息M和标记(i, s)之后,验证Pi⊕h(M)是否等于s,若相等则接受该消息,否则拒绝.这种模式称为WC[H],关于该模式有如下定理.
定理1[9] 如果H是ε-AXU的Hash函数,那么WC[H]是ε-安全的MAC.
但上面的MAC显然是不实用的,因为发送双方要共享一个无限长的串是不现实的.要使得这种构造实用,需要使用一个PRF来产生比特串P,因为一个PRF是带密钥的,这个密钥将提供一个关于所产生的密钥流的描述.只需要将计数值依次输入PRF就可得到伪随机的比特串P.这里计数值也是不允许重复的,否则所产生的伪随机位将变得可预测.
一般地,如果F:{0, 1}k×{0, 1}l→{0, 1}L是一个(t, q, ε′)安全的PRF,H={h:{0, 1}*→{0, 1}L}是一个Hash函数族.这样定义WC[H, F]:通信双方共享的随机密钥是K∈{0, 1}k和一个随机选择的h∈H.这个MAC生成算法是有状态的,它维持一个计数值,该计数值初始值为-1.要认证一个消息M,MAC算法首先增加cnt,并且确保cnt < 2l-1.如果cnt=2l-1就拒绝认证消息,返回REKEY要求发送者重新更换密钥;否则产生消息M的认证标记(cnt,FK(cnt)⊕h(M))并发送给接收者,接收者收到的消息和认证标记是(M′, i, s),要验证该标记,接收者计算FK(i)⊕h(M′)看其是否等于s.关于该构造有如下定理.
定理2[9] 设H是一个ε-AXU的Hash函数族,如果F:{0, 1}k×{0, 1}l→{0, 1}L是一个ε′(t, q)安全的PRF,那么攻击者伪造WC[H, F]的优势最多为ε+ε′.
4 XOR-MAC的安全性证明首先给出信息论中XOR-MAC的定义.设ρ:{0, 1}l→{0, 1}l是随机函数,b是一个给定的常数,b < l.如果M是需要生成标记的消息,把消息M分成长度为l-b-1的块:M=M1M2…Mn,其中Mi=l-b-1. < i > 表示将整数i编码为b-1长的串(这里要求i≤2b-1),那么M的XOR-MAC值T为ρ(0‖r)⊕ρ(1‖<1>‖M1)⊕…⊕ρ(1‖<n>‖Mn),其中r是一个随机的l-1比特的串或者是一个计数值.
这种模式是安全的,文献[2]中已经给出了一个证明,文献[6]中又重新给了一个证明.不过上述证明都很复杂.下面把它看成是一种Carter-Wegman MAC,然后重新给出其证明.
如果将ρ(1‖<1>‖M1)⊕…⊕ρ(1‖<n>‖Mn)看成是一个泛Hash函数,把ρ(0‖r)看成是对该Hash函数的加密,那么这种结构就是WC[H, ρ],它的安全性由定理2得到,下面需要做的是证明该体制所使用的泛Hash函数是ε-AXU的.
首先描述一个“XOR Hash”.给定一个整数值b < l,XOR Hash的定义域D=({0, 1}l-b-1) < 2b,H={h:D→{0, 1}l}是一个函数族,Rand(l, l)表示所有随机函数的集合,其中随机选择一个ρ∈Rand(l, l)意味着随机地选择了一个h.对于任意的M∈D,把M分成l-b-1比特的块M1M2…Mn.定义h(M)如下:
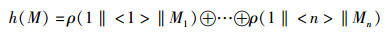
|
XOR Hash是ε-AXU的,一般地,有如下定理.
定理3 设l > 1,b是小于l的整数,那么XOR Hash在定义域D=({0, 1}l-b-1) < 2b上是2-l-AXU的.
证明 根据定义需要证明对于任意的不相同的消息M、M′∈D和常数a∈{0, 1}l,在随机选择函数ρ∈Rand(l, l)的情况下,消息M、M′的Hash值异或之后等于a的概率最多是2-l,也就是要证对于任意的a∈{0, 1}l,有
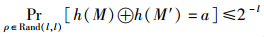
|
(1) |
由于M和M′是不同的2个消息,从而存在2种情况:一种情况是一个消息是另一个消息的前缀;另一种情况是2个消息互相不是对方的前缀.
情况1 不失一般性,假定M′是M的前缀,也就意味着M1=M′1, M2=M′2, …, Mn′=M′n′.因为本身进行异或是0,所以代入后式(1) 重新写为
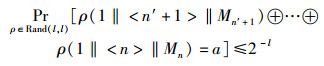
|
(2) |
注意到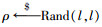
情况2 因为M和M′是不同的2个消息,必然存在某个l-b-1比特长的块不相同.不失一般性,假定M1≠M′1,重新移项后得
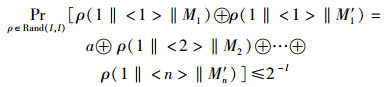
|
因为根据编码规则,1‖<1>‖M1和1‖<1>‖M′1不会与其他的消息块发生碰撞,而且1‖<1>‖M1≠1‖<1>‖M′1,所以这2个值是随机选取的值,从而这个概率是2-l.
综上所述,定理3得证.
在上述体制中,如果r是一个计数器,即为XMACC模式,0‖r不会与消息的输入发生碰撞,每次加密也不会碰撞,因此每个ρ(0‖r)是一个随机的值,也就相当于每次使用一次一密来异或一个2-l-AXU泛Hash函数的输出.由定理1可知,这种构造是2-l安全的,这同文献[2]中的结果是一致的.
如果r是一个随机选择的值,即为XMACR模式,那么虽然0‖r不会与消息的输入发生碰撞,但每次会和自身发生碰撞.如果攻击者询问q次,那么碰撞的概率小于或等于q2×2-l,再加上攻击者进行一次伪造成功的概率2-l,因此该XOR-MAC是q2×2-l+2-l安全的.这也和文献[2]中的结果是一致的.
上面的证明与文献[2]中的结果相比简洁、清晰,这也恰好说明XOR-MAC的好处.
以上所讨论的内容都是在信息论中进行的,借助定理2,可以很容易地推广到复杂性理论中.
5 结束语笔者对XOR-MAC结构进行了分析,将其主体部分定义成泛Hash函数,并证明其是ε-AXU的泛Hash函数,从而可将其整体结构看成是基于泛Hash函数的Carter-Wegman MAC,这样在对安全性进行分析时就可以去除攻击者的自适应性从而得到简洁的安全性证明,同时利用这种新的思想,借助分组密码就可以方便地构造新的消息认证算法.
| [1] | Bellare M, Canetti R, Krawczyk H. Keying hash funtions for message authentication[C]//Crypto 1996. Heidelberg: Springer-Verlag, 1996: 1-19. |
| [2] | Bellare M, Guerin R, Rogaway P. XOR MACs: new methods for message authentication using finite pseudorandom functions[C]//Crypto 1995. Heidelberg: Springer-Verlag, 1995: 15-35. |
| [3] | Bellare M, Kiliany J, Rogaway P. The security of the cipher block chaining massage authentication code[J].Journal of Computer and System Sciences, 2000, 61(3): 362–399. doi: 10.1006/jcss.1999.1694 |
| [4] |
徐津, 温巧燕, 王大印. 一种新的一阶段加密认证模式[J]. 电子学报, 2009, 37(10): 2187–2192.
Xu Jin, Wen Qiaoyan, Wang Dayin. A new one-pass authenticated encryption model[J].Acta Electronica Sinica, 2009, 37(10): 2187–2192. doi: 10.3321/j.issn:0372-2112.2009.10.014 |
| [5] | Black J, Halevi S, Krawczyk H, et al. UMAC: fast and secure message authentication[C]//Crypto 1999. Heidelberg: Springer-Verlag, 1999: 216-245. |
| [6] |
王大印, 林东岱, 吴文玲, 等. XOR-MAC消息认证码的安全性新证明[J]. 中国科学院大学学报, 2006, 23(2): 257–262.
Wang Dayin, Lin Dongdai, Wu Wenling, et al. A new security analysis for XOR message authentication code[J].Journal of University of Chinese Academy of Sciences, 2006, 23(2): 257–262. |
| [7] | Carter L, Wegman M. Universal hash functions[J].Journal of Computer and System Sciences, 1979(18): 143–154. |
| [8] | Stinson D. Universal hashing and authentication codes[C]//Crypto 1991. Heidelberg: Springer-Verlag, 1991: 74-85. |
| [9] | Black J. Message authentication codes [EB/OL]. [2014-02-26]. http://www.cs.colorado.edu/~jrblack/papers/thesis.pdf. |


