与传统的随机移动模型相比,社会网络移动模型旨在生成更符合实际数据统计规律的移动场景.为了从进化的角度研究复杂行为产生的原因,提出了基于遗传算法的移动模型(GAMM),使用“社会收益”与“移动开销”之比作为衡量节点运动轨迹环境适应性的准则,使复杂的移动特性在简单的进化过程中涌现出来.为证明GAMM具有较高的扩展性,提出探索者模型和交通工具模型来满足不同场景的需要,并通过一个网络仿真的实例来研究社会网络移动模型对移动自组织网络路由协议性能的影响.
Compared to traditional random mobility models, a social-based mobility model was proposed, aiming to generate synthetic traces to capture the statistical properties detected from real traces. the driving force of complicated social behaviors from an evolutionary point of view was explored. A genetic algorithm-based mobility model(GAMM) was presented. Using Gain/Cost Ratio as the metric of trace's fitness, complicated movement patterns were emerged from generations of evolutions. Explorer's model and transportation model were presented to show the expandability of GAMM. The influence of social-based mobility model on MANETs network protocols are also investigated by simulation.
节点的移动在很大程度上影响着网络协议的性能.尤其是在机会主义网络和容迟网络环境下,对节点移动特性的准确建模至关重要.传统的随机移动模型忽略了节点移动的社会属性,导致所呈现出的统计规律与实际数据存在差异[1].现有的社会网络移动模型(如侧重地点偏好的SWIM[2]、侧重节点社会关系的CMM[3]和HCMM[4]等)刻意模拟某个社会属性,导致模型适应性与可扩展性差,笔者从复杂的移动模式产生的原因入手,利用遗传算法研究具有高适应能力的移动模型.
1 基于遗传算法的移动模型移动节点通常由人携带或安装在交通工具之上,依附在社会网络之上的大量节点涌现出了复杂的统计规律.在空间属性方面,用户的移动距离满足幂律分布;在时间属性方面,用户在某地的停留时间、访问某地的频率、2个用户见面的时间间隔等属性也满足幂律分布.此外,由于节点移动受地域或时间限制,节点运动的时空属性呈现出截尾特性.
将复杂移动模式的产生原因概括为社会收益与移动开销的均衡,这一行为准则将贯穿本文.具体给出下列定义.
社会收益:个体通过移动到新的地点而获得的收益.不仅包括物质上的收获,如上班的薪水,还包括用户通过完成某个目标而获得的满足感,如购物或看电影,尽管个体需要消费.
移动开销:个体在不同地点间移动所需要支付的开销.不仅包括物质上的花销,如车费,还包括个体在时间上的消耗.
收益/开销比:社会收益与移动开销之比.用来描述个体花费单位移动开销所能获得的社会收益,个体希望收益/开销比能够最大化,将收益/开销比作为遗传算法中衡量个体适应环境能力的准则,指引个体进化出复杂的社会行为.
遗传算法是模拟自然选择和遗传学机理的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,通过基因编码、择优选择、交叉配对、基因变异等一系列过程进化出使适应度函数最大的个体,通过选择合适的适应度函数,可以揭露复杂移动模式产生的原因.下面从3个方面对模型进行介绍.
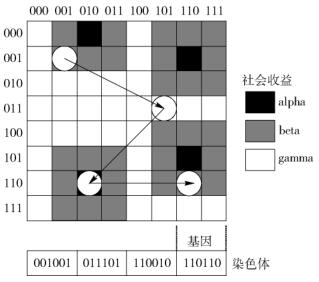
1.1 编码将某节点移动的运动轨迹建模为“染色体”,运动轨迹由一系列坐标组成,将坐标视为染色体中的一个“基因”.将移动区域网格化为WH个边长为S的格子,当某节点的下一个目标格子确定时,节点将在该目标格子中随机选择目的坐标.
以图 1为例,在8×8的已编码网格中,假设某个体的运动轨迹写为[(1, 1), (3, 5), (6, 2), (6, 6)],进行二进制编码后的运动轨迹为[001001, 011101, 110010, 110110].
|
图 1 社会收益与移动开销 |
用收益/开销比作为衡量一条轨迹对环境适应程度的准则,收益/开销比由社会收益和移动开销两部分组成.
假设活动区域内每一个格子具有的社会收益为0≤g(i, j)≤1, 其中i=0, 1, …, W-1, j=0, 1, …, H-1,一条含有N个基因的染色体C由N个编码后的坐标组成,表示为
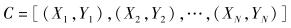
|
轨迹C的社会收益gs(C)定义为每个基因的社会收益之和,即
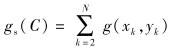
|
(1) |
其中,g(x1, y1)被忽略了,因为初始节点的社会收益并不是由于移动而获得的.
将社会收益划分为3个离散的等级,分别为α、β和γ(1≥α>β>γ≥0).在现实中,一个高社会收益的地区(社区中心)往往被低社会收益地区包围.当α=1, β=0.5, γ=0时,图 1中运动轨迹的社会收益为1.5.
节点的每一步移动都会产生移动开销,为叙述方便,首先假设移动开销与移动距离成正比,且比例系数为1,在2.2节将对两者的关系进行更为细致的讨论.轨迹C的移动开销cm(C)可以定义为每一步移动距离之和,即
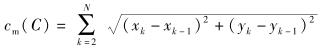
|
(2) |
运动轨迹C的收益/开销比g/c(C)定义为社会收益与移动开销的比值,即
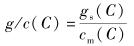
|
(3) |
以图 1所示的移动场景和节点轨迹为例,轨迹的移动开销为4.47+4.24+4=12.71,轨迹的收益/开销比为1.5/12.71=0.118.
需要指出的是,在编码和适应度计算的过程中都没有出现具体的数值,例如场景中每个格子的大小、社会收益的单位、移动开销与移动距离的比例系数等,这样做的目的是为了提高算法的可扩展性,使移动模型能够应用到不同的场景中.
1.3 控制参数的选择控制参数是指在遗传算法的选择、交叉配对、基因变异等过程中涉及的参数,如选择算子、交叉算子、变异算子等.这里对遗传算法的原理和各算子的原理不予赘述.经试验发现,算子仅对算法的收敛速度有一定影响,对生成场景的性能影响较小.
选择是在群体中选择生命力强的个体产生新的群体的过程,遗传算法中使用选择算子根据适应度对群体中的个体进行优胜劣汰操作.这里使用随机采样(SUS,stochastic universal sampling)作为选择算子,与传统的轮盘赌选择方法相比,SUS算子利用单一的随机值选出多个个体,能够提高轮盘赌算子的公平性.
交叉是按较大的概率从群体中选择2个染色体,交换2个染色体中的某几段基因,交叉产生的子代继承了父代个体中的优秀基因,交叉算子指的是父代个体交换基因的方式.研究中采用均匀交叉作为交叉算子,与传统的单点交叉和两点交叉相比,均匀交叉算子允许父代染色体机会均等的贡献整段基因,将偏差降至最低.
变异是以较小的概率对染色体上的某个或某段基因的值进行改变,进而产生新的变异后个体.在对遗传算法的应用中忽略了变异过程,原因是通过反复的测试发现,在本文的模型下,变异并没有提高最终代个体的适应度,反而降低了进化的收敛速度.
2 GAMM模型性能分析利用Matlab的遗传算法工具箱实现了GAMM,生成节点运动轨迹数据,通过分析运动轨迹数据的时间、空间属性来研究GAMM模型的性能.移动模型参数如表 1所示.
|
|
表 1 移动模型参数表 |
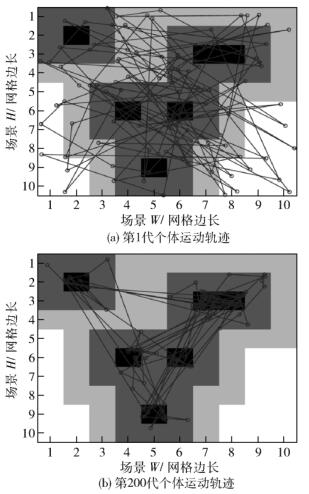
某一运动轨迹从第1代到第200代的进化过程如图 2所示.在第1代运动轨迹中,节点随机选择下一个目标格子,这样的轨迹可以用来模拟传统的随机移动模型.在适应度函数的约束下,随着简单进化,复杂的移动行为产生了,个体的运动逐渐集中在几个高社会收益地区,偶尔在高收益地区外围活动. 图 2直观地示出了模型的特点,下面从3方面深入分析运动轨迹的属性.
|
图 2 运动轨迹进化示意图 |
在自然进化过程中,从无序到有序的进化是熵减过程,使用位置熵来描述节点选择下一步目标格子的随机性,进而研究某条轨迹的环境适应度与移动随机性的关系.定义运动轨迹的位置熵为
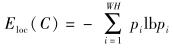
|
(4) |
其中pi(i=1, 2, …, WH)表示格子i被某节点选作下一步目标格子的概率.
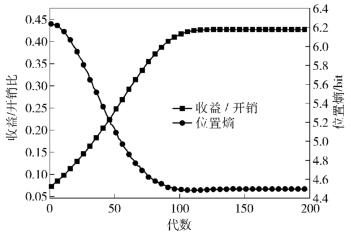
图 3显示了收益/开销比与位置熵的进化过程.可以看出,从第1代进化开始,适应度低的个体逐渐被淘汰,而移动开销低、社会收益高的移动策略逐渐产生,节点更趋向于选择在高社会收益地区附近移动,导致位置熵的降低.在100代时,个体已经进化出最优的运动轨迹.位置熵的衰减速度与收益开销的增加速度是同步的,调整收益/开销比可以影响进化的速度.
|
图 3 收益/开销比与位置熵 |
通过分析节点每一步移动距离的互补累积分布函数来研究运动轨迹的空间属性.为体现GAMM模型的可扩展性,首先提出2个与空间属性有关的扩展模型.
1) 探索者模型.在现实中,用户对新地点的探索欲望是不同的,通过对式(1) 的重新修正,将GAMM模型扩展为探索者模型,修正后的社会收益函数为
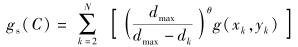
|
(5) |
其中dk表示从格子(xk-1, yk-1)移动到(xk, yk)的距离,探索因子θ(θ>1) 表示个体偏好遥远地点的程度.
2) 交通工具模型.在现实中,用户会根据目标的远近选择合适的移动方式,因此将移动开销建模为移动距离的分段函数.通过对式(2) 的修正,扩展后的交通工具模型如式(6) 所示.
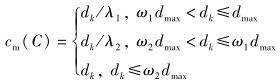
|
(6) |
其中:开销削减因子λi(λi>1) 表示交通工具能够减小移动开销的程度,交通工具的有效作用范围可以通过ωi(0 < ωi < 1) 来调整.
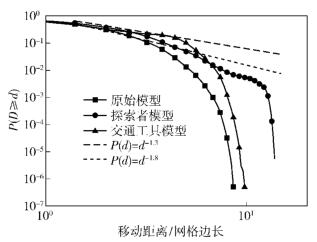
在探索者模型中,取θ=1.4、dmax=15,在交通工具模型中,取λ1=3、ω1=0.5、λ2=2、ω2=0.3,图 4示出了移动距离的互补累积分布函数,轨迹分别由原始模型、探索者模型、交通工具模型产生.
从图 4中可以看出,移动距离的分布满足截尾幂律分布,用户倾向于选择离出发地比较近的地点作为下一步移动的目标,但偶尔用户为了获得更大的社会收益而选择移动到较为偏远的地点.探索者模型与原始模型相比,截尾的趋势更加明显,这是因为虽然探索者模型减小了移动开销,但受场景大小的限制,曲线的末端变得陡峭.交通工具模型受ω1与ω2的影响呈现明显的分段特性.
|
图 4 移动距离的互补累积分布函数 |
在时间属性方面,主要研究用户接触时间(CT,contact time)和用户接触间隔时间(ICT,inter contact time)的分布特性.用社区内接触时间来描述属于同一个社区的2个个体从某次见面到分手的时间,用社区内接触间隔时间来描述属于同一个社区的2个个体从分手到再次见面的时间.社区是指具有相同地点偏好的用户所组成的群体,在模型中可以用目标格子的社会收益来表示个体对地点的偏好.假设网络中有Ng个社区,每个社区的个体数为Np.属于同一个社区的个体具有相同的社会收益矩阵,且假设个体的重要程度完全相同.
取Ng=5、Np=20,传输范围为2.5倍的网格边长,通过分析GAMM生成的100条运动轨迹,得到时间属性的分布规律如图 5所示.
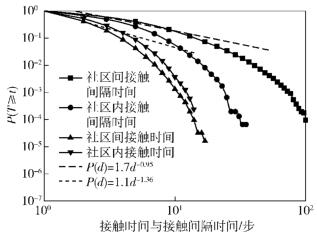
|
图 5 接触时间与接触间隔时间的互补累积分布函数 |
从图 5中可以看出,接触时间与接触间隔时间的分布同样满足截尾幂律分布.比较接触时间与接触间隔时间可以发现,用户处于非接触状态的时间要更长.分别比较社区内与社区间的曲线可以发现,属于同一社区的用户更具有相似的行为规律,因而接触的概率更大,接触间隔时间则相对较小,这更有利于数据的传输.
3 移动模型对网络协议性能的影响研究节点移动模型的意义在于把握社会网络中节点的移动规律,在此基础上更准确地仿真网络协议的性能[5].选取在网络仿真中被广泛使用的随机路点模型(RWP,random way point)作为随机移动模型的代表,由于RWP模型忽略了节点的社会属性,导致研究者对网络性能的估算存在偏差.笔者在网络仿真软件NS2.34上针对移动模型对网络协议性能产生的影响展开研究.
在1 km×1 km的场景中分布着30个节点,节点的传输距离为250 m.在网络中选取10对源宿节点建立10条CBR数据流,发包速率为10包/s.仿真场景的MAC层使用IEE802.11协议,路由层使用AODV协议.在RWP模型和GAMM模型中,节点的移动速度在0和10 m/s间随机选择.
为研究群体行为对网络性能的影响,在GAMM模型中,将30个节点分为3个社区,每个社区中的10个节点具有相同的社会收益矩阵.在“GAMM社区内”子场景中,源宿节点分别来自相同的社区,而“GAMM社区间”子场景则完全相反,源宿节点分别来自不同的社区.
如图 6所示,与GAMM模型产生的移动场景相比,RWP移动模型下仿真得到的吞吐量比GAMM模型低,而RWP得到的平均端到端时延则比GAMM高.总的来说,当考虑社会属性对网络的影响时,使用RWP模型总会低估网络协议的性能.这是由于RWP模型假设节点随机移动且彼此独立,则节点的接触时间要比实际更短,导致数据传输的中断概率更大.在GAMM模型中,社区内的性能要优于社区间的性能,这是由于相似的行为规律为社区内的节点创造了更多的接触机会.
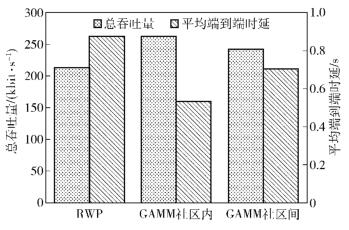
|
图 6 移动模型对网络协议性能的影响 |
在社会网络中,传统的随机移动模型生成的移动场景并不能准确反应用户的行为规律,笔者提出的社会网络移动模型旨在生成具有社会属性的节点移动场景,使运动轨迹的时间属性、空间属性更加符合现实中用户的运动规律.使用遗传算法深入研究了复杂移动行为规律产生的原因,并通过探索者模型和交通工具模型证明了GAMM模型具有较高的可扩展性.研究了网络模型对移动自组织网络协议性能的影响.下一步将把场景的应用范围扩展到容迟网络,并深入研究社会关系对移动模型的影响.
| [1] | Yoon J, Liu Mingyan, Noble B. Random waypoint considered harmful [C]//2003 IEEE INFOCOM. San Francisco, CA: IEEE Press, 2003: 483-502. |
| [2] | Mei A, Stefa J. SWIM: a simple model to generate small mobile worlds [C]//2009 IEEE INFOCOM. Brazil: IEEE Press, 2009: 2106-2013. |
| [3] | Musolesi M, Mascolo C. Designing mobility models based on social network theory[J]. ACM Sigmobile Mobile Computing and Communications Review, 2007, 11(3): 59–70. doi: 10.1145/1317425 |
| [4] | Boldrini C, Passarella A. HCMM: modeling spatial and temporal properties of human mobility driven by users social relationships[J]. Computer Communications, 2010, 33(9): 1056–1074. doi: 10.1016/j.comcom.2010.01.013 |
| [5] |
刘元安, 唐碧华, 胡月梅. Ad hoc网络中的路由算法[J]. 北京邮电大学学报, 2004, 27(2): 1–7.
Liu Yuan'an, Tang Bihua, Hu Yuemei. Routing algorithms in mobile Ad hoc networks[J]. Journal of Beijing University of Posts and Telecommunications, 2004, 27(2): 1–7. |