对于每个用户均配置两根天线的X信道,提出了一种新的空时码传输方案.每个用户采用速率为2的空时分组码(R2-STBC),通过合理地设计R2-STBC的发送方式和预编码,使接收端对接收信号进行线性处理后消除了多用户干扰.与相同场景中已有的空时码传输方案相比,所提方案不但节省了反馈量,还提高了传输效率.仿真结果显示,所提方案的可靠性显著优于相同场景中的已有方案.
A new space-time coded transmission scheme is proposed for X channel with two antennas at each user. Each user employs rate-2 space-time block code (R2-STBC). The multi-user interference is eliminated by proper design of transmission method of R2-STBC and pre-coding at the transmitter. The feedback amount is reduced and the transmission efficiency is higher as well, compared with the existing scheme for the same scene. Simulation results demonstrate that the reliability of the proposed scheme significantly outperforms the existing scheme.
多输入多输出(MIMO, multi-input multi-output)技术的传输方案可以分为两类[1]:1) 空间分集方案;2) 空间复用方案.研究较多的空间分集方案是空时分组码(STBC, space-time block code)[2]. STBC获得了分集增益,但是不能获得复用增益.于是,有学者提出了完美空时分组码,兼顾分集增益和复用增益[3].速率为2的空时分组码(R2-STBC, rate-2 space-time block code)是完美空时分组码的一种[4].
MIMO技术分为单用户MIMO和多用户MIMO.每个用户配置多根天线的X信道是一种多用户MIMO系统[5].由于X信道中2个发送端不可相互协作,接收端存在多用户干扰,影响系统的可靠性.
干扰对齐可以消除X信道中的多用户干扰[6-7],然而该方案的分集增益较低. Li Feng等[8]将空时编码及其预编码引入X信道,获得了空时编码带来的分集增益,其可靠性优于相同场景中的干扰对齐方案.然而,该方法的使用范围有限,发送天线的个数不能低于5,且接收天线的个数不低于3[8]. Li Liangbin等[9]也提出了采用空时编码及其预编码来消除X信道中的多用户干扰.然而该方案需要大量的反馈信息.
为了降低反馈量,提出该场景中一种新的空时码传输方案,每个用户采用速率为2的空时分组码,并且每个编码矩阵连续发送2次.通过对接收信号进行加减操作减少了相互干扰码字的数量,再通过合理地设计预编码消除了多用户干扰.与文献[9]中的方案相比,所提方案不但减少了一半反馈量,还提高了传输效率.仿真结果显示,在独立的瑞利信道且高斯白噪声的条件下,采用16QAM调制且误比特率(BER, bit error rate)为10-4时,所提方案比文献[9]中的方案获得了大约5 dB的增益.
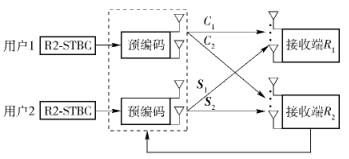
1 系统模型系统模型(见图 1)包含2个用户和2个接收端Ri(i=1, 2),每个用户配置2根天线,每个接收端配置N根天线. Hi是用户1~Ri的信道矩阵,Gi是用户2~Ri的信道矩阵,它们的阶数均为N×2.
|
图 1 系统模型 |
2个用户均采用速率为2的空时分组码,ci(i=1, 2, …, 8) 和si是调制信号,码字Ci(i=1, 2) 和Si分别为
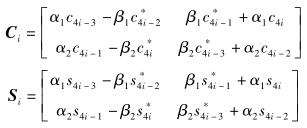
|
其中:α1、α2、β1和β2是实数,它们满足α12+β12=1且α22+β22=1[4].用户1将码字Ci发送给Ri,用户2将码字Si发送给Ri.
信息的传输分为2个步骤.
步骤1 用户1对Ci进行预编码,得到AiCi,并将码字A1C1+A2C2发送到接收端;用户2对Si进行预编码,得到BiSi,并将码字B1S1+B2S2发送到接收端. R1的接收信号和R2的接收信号分别表示为
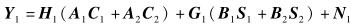
|
(1) |
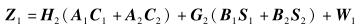
|
(2) |
其中: N1和W1为噪声矩阵,阶数均为N×2;Ai和Bi分别是Ci和Si的预编码矩阵,它们的阶数均为2×2.为了保证发射功率不变,‖ Ai‖2=‖ Bi‖2=0.5.
步骤2 在相同的时间内,用户1和用户2分别将码字A1C1-A2C2和B1S1-B2S2发送到接收端,R1的接收信号和R2的接收信号分别表示为
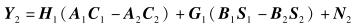
|
(3) |
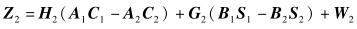
|
(4) |
其中: N2和W2为噪声矩阵,它们的阶数均为N×2.
所提方案实施的前提是在每个编码矩阵的2次传输时间内,信道保持不变.
所提方案在4个时隙内传输了16个调制符号,其传输效率为4 symbols/channel use.尽管所提方案中每个编码矩阵都传输了2次,其传输效率仍是文献[9]方案的1.5倍.
由式(1)~式(4) 可得出
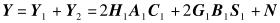
|
(5) |
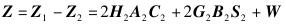
|
(6) |
其中: N=N1+N2,W=W1-W2.
由式(5) 可看出,对R1的接收信号进行相加运算后消除了C2和S2,而C1和S1相互干扰.由式(6) 可看出,对R2的接收信号进行相减运算后消除了C1和S1,而C2和S2相互干扰.即对接收信号进行加减操作后减少了相互干扰的编码矩阵的数量.
下面以消除Ci和Si之间的干扰为目标,给出预编码矩阵Ai和Bi的设计方法,i=1, 2.
2 预编码矩阵的设计分别用amni和bmni表示Ai和Bi的第m行第n列的元素,m, n, i=1, 2.分别用hmni和gmni表示Hi和Gi的第m行第n列的元素,m=1, 2, …, N,n, i=1, 2.
为减少反馈信息,假定Ai的第1列和第2列相同且Bi的第1列和第2列也相同,i=1, 2,则HiAi和GiBi表示为
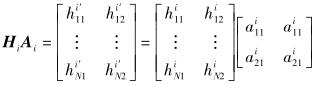
|
(7) |
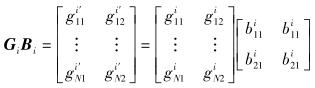
|
(8) |
分别用dmn和emn表示矩阵H1A1C1和G1B1S1的第m行第n列的元素,m=1, 2, …, N,n=1, 2,根据文献[4]中的式(13) 可得

|
(9) |
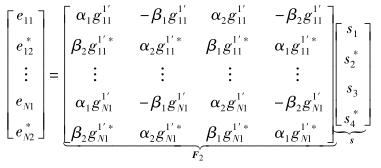
|
(10) |
F1和F2的阶数均为2N×4.
根据式(5)、式(9) 和式(10) 可以得出
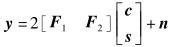
|
(11) |
其中: y = [ y11, y12*, …, yN1, yN2* ]T, n = [ n11, n12*, …, nN1, nN2* ]T,ymn和nmn分别为矩阵Y和N的元素.若F1的所有列与F2的所有列相互垂直,则c和s在传输过程中保持正交,从而可消除C1和S1之间的干扰.
用fi表示F1的各列,i=1, 2, 3, 4,用fk表示F2的各列,k=5, 6, 7, 8.计算可得
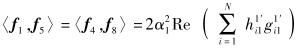
|
(12) |
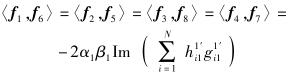
|
(13) |
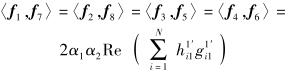
|
(14) |
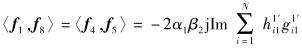
|
(15) |
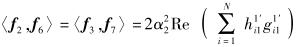
|
(16) |
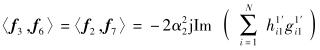
|
(17) |
其中:j= 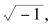
由式(12)~(17) 可看出,若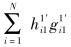
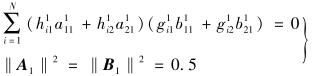
|
(18) |
方程组包含3个方程、4个未知量,有无数组解.
同理可以得出C2和S2之间互不干扰时A2和B2满足的条件.
所提方案中预编码矩阵的每列相同,只需要反馈预编码矩阵的第1列的元素.因此,所提方案比文献[9]中的方案减少了一半反馈信息.
3 译码方法将式(11) 两端分别乘以[F1T F2T]T可得
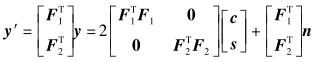
|
其中0为4×4的零矩阵.从而R1可以分别译码2个发送端发送给R1的有用信号,具体译码过程如下.
步骤1 R1对其接收信号进行相加操作,得到Y=Y1+Y2,然后得到Y的等效表达形式y;
步骤2 R1根据信道矩阵和预编码矩阵计算得到H1A1和G1B1,并根据H1A1和G1B1得到F1和F2;
步骤3 R1处理y,得到y′=[ F1T F2T]Ty;
步骤4 以y′的前4列作为等效接收信号,以2F1TF1和2F2TF2作为等效信道矩阵,分别译码用户1和用户2发送给R1的有用信号;
R2的译码过程与上述步骤类似.步骤4和步骤5可采用文献[4]中给出的译码方法,其译码复杂度与调制阶数的平方成正比.文献[9]中的译码复杂度与调制阶数成正比,这是所提方案的不足之处.
4 仿真结果假定信道服从独立的瑞利分布,噪声为高斯白噪声,N=2,α1、α2、β1和β2的取值有无数个,此处不妨假定他们的取值使得R2-STBC的编码增益达到最大值,即α1=β2=sin (arctan (2)),α2=β1=cos (arctan (2)).
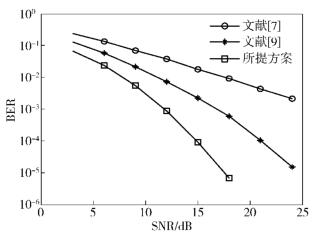
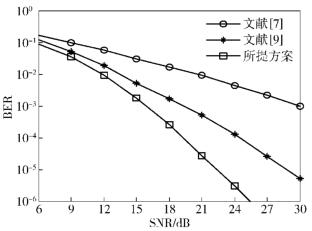
图 2和图 3分别给出了调制方式为4QAM和16QAM时3种方案的BER曲线.图中的横坐标表示每个用户的信噪比.可以看出,所提方案的BER曲线显著低于文献[7]和文献[9]中的方案. BER为10-4,且调制方式分别为4QAM和16QAM时,所提方案的增益分别为6 dB和5 dB.
|
图 2 调制方式为4QAM时3种方案的BER |
|
图 3 调制方式为16QAM时3种方案的BER |
对于每个用户均配置两根天线的X信道,已有的空时码传输方案和所提方案都通过发送端预编码以及接收端的线性处理消除了多用户干扰,而所提方案减少了一半反馈信息,并且其传输效率是文献[9]中方案的1.5倍.仿真结果显示,所提方案的可靠性显著优于文献[9]的方案.
| [1] | Kaiser T, Zheng F, Dimitrov E. An overview of ultra-wide-band systems with MIMO[J]. Proceedings of the IEEE, 2009, 97(2): 285–312. doi: 10.1109/JPROC.2008.2008784 |
| [2] | Gesbert D, Shafi M, Shiu D. From theory to practice: an overview of MIMO space-time coded wireless systems[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(3): 281–302. doi: 10.1109/JSAC.2003.809458 |
| [3] | Oggier F, Rekaya G, Belfiore J C, et al. Perfect space-time block codes[J]. IEEE Transactions on Information Theory, 2006, 52(9): 3885–3902. doi: 10.1109/TIT.2006.880010 |
| [4] | Rabiei P, Al-Dhahir N, Calderbank R. New rate-2 STBC design for 2 TX with reduced-complexity maximum likelihood decoding[J]. IEEE Transactions on Wireless Communications, 2009, 8(4): 1803–1813. doi: 10.1109/TWC.2009.071323 |
| [5] | Maddah-Ali M, Motahari A, Khandani A. Communication over MIMO X channels: Interference alignment, decomposition, and performance analysis[J]. IEEE Transactions on Information Theory, 2008, 54(8): 3457–3470. doi: 10.1109/TIT.2008.926460 |
| [6] | Huang C, Cadambe V R, Jafar S A. Interference alignment and the generalized degrees of freedom of the x channel[J]. IEEE Transactions on Information Theory, 2012, 58(8): 5130–5150. doi: 10.1109/TIT.2012.2201343 |
| [7] | Jafar S, Shamal S. Degree of freedom region for the mimo x channel[J]. IEEE Transactions on Information Theory, 2008, 54(1): 151–170. doi: 10.1109/TIT.2007.911262 |
| [8] | Li Feng, Jafarkhani H. Space-time processing for x channels using precoders[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1849–1861. doi: 10.1109/TSP.2011.2181504 |
| [9] | Li Liangbin, Jafarkhani H, Jafar S A. When alamouti codes meet interference alignment: transmission schemes for two-user x channel [C]//2011 International Symposium on Information Theory (ISIT2011). Petersburg: IEEE Press, 2011. |


