2. 中国电子系统工程总公司, 北京 100840
提出了一种基于神经网络的电力通信网风险评估算法——基于二分法的学习速率自适应BP(back propagation)神经网络算法.该算法在网络训练过程中使用二分法调整学习速率,使得学习速率在训练过程中不断向最优化方向自动调整.仿真结果表明,收敛速度、误差精度和训练时间等算法性能得到了优化.
2. China Electronic Systems Engineering Corporation, Beijing 100840, China
An improved back propagation neural network algorithm based on dichotomy was proposed for assessment of electric power communication network risk. The dichotomy was used to adjust the learning rate in the training process. It helps to change the learning rate automatically to the direction of optimization. Simulation shows that the improved algorithm's performance is optimized, such as convergence rate、error accuracy and training time.
随着电力通信网的发展,大量的电力系统业务需要通过电力通信网传输信息,电力系统生产部门对电力通信网的可靠性要求也越来越高,因此,对电力通信网进行风险评估具有重要意义[1].笔者提出一种基于二分法的学习速率自适应BP神经网络算法(DABP, BP algorithm based on dichotomy adjust)作为电力通信网风险评估方法.该算法使用二分法自适应调整学习速率,不仅实现简单,算法的收敛速度、误差精度及训练时间都优于传统BP算法.将改进算法作为风险评估算法应用于电力通信网风险评估仿真实验中,通过评估结果的对比分析,验证了改进算法具有更优的收敛速度、误差精度及训练时间.
1 基本理论及算法改进 1.1 基本BP算法BP神经网络是3层前馈BP网络,包括1个输入层、1个隐含层、1个输出层[2].上下层之间实现全连接,而每层节点之间无连接. BP神经网络算法是一种多层网络的“逆推”学习算法,从输入层到隐层、从隐层到输出层的传递函数均为sigmoid函数:
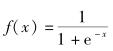
|
(1) |
BP神经网络的学习过程如下[3].
1) 前向传播过程
输入层的输入与输出:
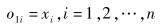
|
(2) |
其中:xi为输入层节点i的输入值,o1i为输入层节点i的输出值,n为输入层节点数.
隐层的输入与输出:
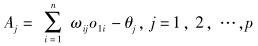
|
(3) |
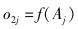
|
(4) |
其中:Aj为隐层节点j的输入值,ωij为输入层第i个节点与隐层第j个节点的连接权值,θj为隐层第j个节点的阈值,n为输入层节点数,p为隐层节点总数,o2j为隐层节点j的输出值.
输出层的输入与输出:
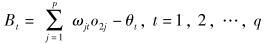
|
(5) |
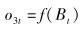
|
(6) |
其中:Bt为输出层节点t的输入值,ωjt为隐层第j个节点与输出层第t个节点的连接权值,θt为输出层第t个节点的阈值,q为输出层节点总数,o3t为输出层节点t的输出值.
2) 反向传播过程
反向传播过程的基本思想是:o3t为输出层的节点t的实际计算输出,通过o3t与所期望的输出dt之间的误差反向传播来修改各权值.误差值定义为
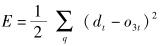
|
(7) |
其中:E为误差值,dt为输出层节点t的期望输出值,q为输出节点总数,o3t为输出层节点t实际计算输出.
对于每个训练样例,网络的权值沿E函数梯度方向下降修正,任意两层节点之间权值ωab的变化量为
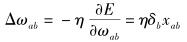
|
(8) |
其中:Δωab为权值ωab的变化量,η为学习速率,xab为从任意一层节点a到节点b的输入. δb为权值调整量,输入层与隐层之间的δb和隐层与输出层之间δb的计算方法并不相同,计算方法如下.
输出层与隐层之间的权值变化量Δωjt为
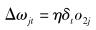
|
(9) |
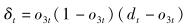
|
(10) |
输入层与隐层之间的权值变化量Δωij为
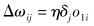
|
(11) |
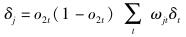
|
(12) |
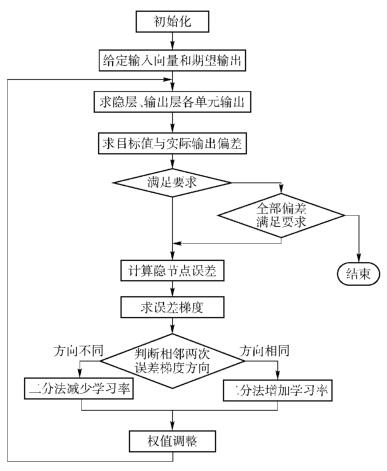
从BP算法公式中可以看出,学习速率η决定了收敛速度,适当地选取学习速率η可以明显优化提高性能[4-5].因此,提出一种DABP算法.该算法的实质是:使学习速率根据网络训练的状态自动调整,若相邻两次调整方向相同则使用二分法加大学习速率η,若相邻两次调整方向不同则使用二分法减少学习速率η,从而达到在训练过程中不断优化学习速率的目的. DABP算法可以使得学习速率在训练过程中根据网络状态自适应调整,促使学习速率不断向最优方向改变,从而改善传统BP算法误差下降缓慢、调整时间长、收敛速度慢等缺点,使得算法性能得到大大改善. DABP算法的算法流程图如图 1所示.
|
图 1 DABP算法流程 |
DABP算法的学习率调整过程如下.
1) 设置η的取值范围为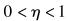
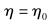
|
(13) |
2) 如果相邻2次调整的梯度之积为正,说明相邻两次调整的梯度方向相同,收敛情况较好,可以使用二分法加大学习速率,使其调整速率加快:
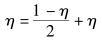
|
(14) |
式(14) 的含义是:在η与1之间取中值,将该中值作为η的取值.
3) 如果相邻2次调整的梯度之积为负,说明相邻2次调整的梯度方向相反,在2次调整之间出现了极值点,此时学习速率过大,使得上一次调整时越过了极值点,因而需要使用二分法减小学习速率,提高误差精度.
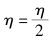
|
(15) |
式(15) 的含义是:在η与0之间取中值,将该中值作为η的取值.
2 实验仿真 2.1 电力通信网风险评估指标体系电力通信网中包含各种各样的通信设备,各个部分组织在一起,构成了多技术、多层次的复杂网络结构.因而构建电力通信网的风险评估指标体系时要考虑众多的风险因素,分为4类,包括设备因素、业务因素、环境因素以及运行管理因素.风险评估指标体系如表 1所示.
|
|
表 1 电力通信网风险评估体系 |
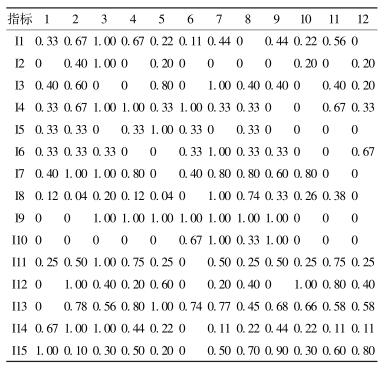
表 1中各评估指标的取值由某电力通信网12个月的运行数据以及当年的气象数据确定[6],风险值由某电力通信网风险评估标准计算得出.其中I1~I6是取值为当月该通信设备故障数,I7~I8和I11~I15为当月统计数据,I9~I10为当月气象数据,其余指标均根据运行数据确定.在统计了指标数据后,将指标数据归一化处理:
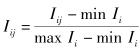
|
(16) |
其中:i表示指标序号,j表示月份.归一化后各指标的输入数据如表 2 所示.
|
|
表 2 电力通信网1~12月风险指标值 |
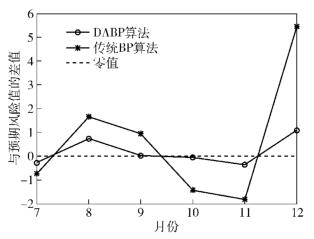
选用DABP算法作为电力通信网风险评估方法.根据给出的电力通信网风险评估指标体系,确定输入层节点为15个,输出层节点为1个.输入层节点的输入值是风险评估指标的取值,而输出层节点的输出值为风险评估值.关于隐层节点个数的确定,理论上没有明确的规定,往往是需要根据设计者的经验和多次实验来确定,并且与问题所要求的学习误差、输入单元数目和输出单元数目都有直接关系.使用目前一种广泛使用的确定隐层节点的方法:
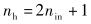
|
(17) |
其中:nh为隐层节点个数,nin为输入层节点个数.
因此应用的隐层节点数为31个.传统的BP算法学习速率和DABP算法的初始学习速率均设定为0.05,误差限定为小于0.01.
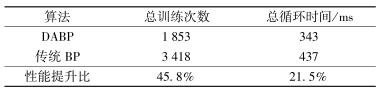
2.3 仿真结果将指标数据分为2组,使用前6个月数据训练BP神经网络,使用后6个月数据评估风险值.通过使用传统的BP算法和DABP算法对数据进行训练,得出2种算法的性能值,如表 3所示.
|
|
表 3 算法性能值 |
2种算法的收敛速度对比如图 2所示.
|
图 2 算法收敛速度对比 |
从图 2可见,随着训练次数的增加,传统BP算法的误差下降较为缓慢,并且一度陷于极小点中.而DABP算法一直保持较快的误差下降速率,收敛迅速,收敛速度得到明显优化.
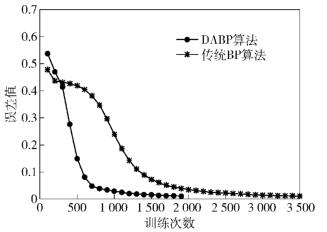
传统BP算法得出的风险值和DABP算法得出风险值与预期风险值的误差如图 3所示.
|
图 3 算法误差值对比 |
图 3中虚线表示与预期风险值没有差值,是零值线,预期风险值为根据某电力通信网风险评估标准计算得出.综合6个月的风险值误差比较,使用传统BP算法进行评估后得到的风险值与预期风险值之间的差值较大,使用DABP算法进行评估后得到的风险值与预期风险值更接近,差值较小,因而DABP算法误差精度也更优.
3 结束语提出一种DABP算法作为电力通信网风险评估方法.该算法在训练过程中不再使用固定的学习速率,而是根据训练状态使用二分法动态调整学习速率,使得学习速率在训练过程中不断向最优化方向自动调整.然后,将DABP算法应用于电力通信网风险评估中,使用某电力通信网12个月的运行统计数据对电力通信网风险评估指标进行仿真实验,通过评估结果的对比分析,验证了本文提出的评估方法不仅实现简单,而且具有更优的收敛速度、误差精度及训练时间.在DABP算法的神经网络训练后期,误差降低速度开始减缓,这是由于BP算法中的梯度下降法在接近最小值时调整能力下降.如DABP算法与其他改进方法结合,使得在误差接近最小值时能快速收敛,则算法性能将得到进一步优化.如何改进DABP算法,还需进一步研究.
| [1] | Gao Huisheng, Feng Lina. Risk evaluation of the electric power communication network based on compatibility Rough-Fuzzy set[C]//Intelligent Systems and Applications, 2009. 2009: 1-4. http://www.buptjournal.cn/CN/abstract/abstract1838.shtml |
| [2] | Zhang Yichuan, Qiao Lifang, Qi Anguo. An evaluation method of wasteland landscape restoration plan based on BP neural network model[J]. Journal of Food Agriculture & Environment, 2012(10): 1093–1095. |
| [3] | Jing Guolin, Du Wenting, Guo Yingying. Studies on prediction of separation percent in electrodialysis process via BP neural networks and improved BP algorithms[J]. Desalination, 2012(291): 78–93. |
| [4] | Zhang Feng, Li Pengfeng, Hou Zengguang. sEMG-based continuous estimation of joint angles of human legs by using BP neural network[J]. Neurocomputing, 2012(78): 139–148. |
| [5] | Jin Juliang, Wei Yiming, Zou Lele, et al. Forewarning of sustainable utilization of regional water resources: a model based on BP neural network and set pair analysis[J]. Natural Hazards, 2012, 62(1): 115–127. doi: 10.1007/s11069-011-0037-9 |
| [6] | Zeng Qingtao, Qiu Xuesong, Gao Zhipeng, et al. Adaptive T-S FRBF-based risk assessment method for electric power communication network[J]. Journal of Information and Computational Science, 2012(10): 3063–3070. |