有限状态机作为星载数字系统实现控制逻辑的重要手段,其稳定性直接影响系统的正常运行.空间辐射环境所造成的单粒子翻转效应会导致有限状态机不稳定.目前常用的容错方法适于处理状态机的1位翻转错误,而具有高可靠性要求的系统还需要能处理2位翻转错误.基于(16, 8) 准循环码的有限状态机容错设计方法,可实时纠正1位或2位翻转错误,检测到3位翻转错误,使有限状态机拥有更高的可靠性.此方法同时具有硬件易实现,系统延时小等优点.
The stabilities of finite-state machine (FSM) seriously affects the normal operation of satellite borne system, and is important for control logic. Single event upset caused by space radiation environment often leads to FSM instabilities. Current fault-tolerant methods can correct single error. However, the correction of double errors for those high reliability systems is also necessary. A new design of field program gate array(FPGA) based on (16, 8) quasi-cyclic code was presented. With advantages of high reliability, uncomplicated hardware and short delay. The design can correct single or double errors, and detect triple errors as well.
空间高能粒子对电子元器件的单粒子效应(SEU,single event upset)会造成如存储信息丢失、控制状态改变等后果,甚至导致设备失效.从SEU造成星载数字系统失效的数据来看,大约99%属于1位翻转错误,剩余1%左右的为2位或多位翻转错误[1].随着空间科学技术的发展,卫星在轨时间增长,2位翻转错误如不能及时纠正,其对系统不良影响的累积效应也不容忽视.
可编程门阵列(FPGA,field program gate array)拥有丰富的逻辑资源和存储资源,广泛应用于星载数字系统,有限状态机(FSM,finite-state machine)作为FPGA内部实现系统控制的主要方式,可靠运行十分必要.但基于SRAM(static RAM)工艺的FPGA易受SEU的影响,因此,研究FPGA内FSM的抗SEU 2位翻转的能力,对星载系统的可靠性设计有重要意义.
1 FSM容错设计方式及问题通常的FSM容错设计方法是利用空间冗余,比较典型的如三模冗余(TMR,triple modular redundancy). TMR可以有效抵御1位翻转错误的发生,但对2位翻转则无法解决.
FPGA内置RAM抗SEU能力要高于其逻辑资源的抗SEU能力,近年有学者提出利用FPGA内置RAM实现FSM[2],再通过对状态进行编码的方式进行检测纠错[3],从而实现FSM抗SEU.常用的汉明码纠错只能纠正1位翻转错误.纠正多位突发错误的编码,如RS码等,存在编译码过程复杂,实时性差的缺点.相比之下,(16, 8) 准循环码具有低复杂度和高实时性的优点,可以纠正1位和2位错误翻转,检测3位错误翻转,曾被用于增强星载平台数据传输的稳定性[4].该编码结构易于FPGA实现,可引入高可靠容错FSM的设计之中.
2 基于(16, 8) 准循环码的FSM 2.1 (16, 8) 准循环码的原理所谓准循环码,就是每个码字都是前一个码字的移位,一个码字循环移动n位后,仍然是代码矩阵中的一个码字. (16, 8) 准循环码是线性编码,其最小编码距离为dmin=5,能纠正的最小错误位数为
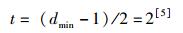
|
1) 编码.通常的(16, 8) 准循环码的生成矩阵形式为c=[I8:G],其中I8为单位矩阵,G为校验矩阵.选取校验矩阵G作为编码部分.

|
(1) |
设原码为m=(m0, m1, m2, m3, m4, m5, m6, m7),根据
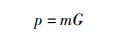
|
(2) |
算出校验码p=(p0, p1, p2, p3, p4, p5, p6, p7),其编码规则如式(3) 所示.原码和校验码构成了完整的(16, 8) 准循环码编码n=[p, m].
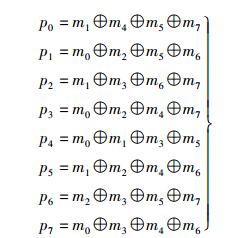
|
(3) |
2) 译码. (16, 8) 码的译码需要读取完整的编码n′=[p′, m′].其中p′为校验码p的读取值,m′为原码m的读取值.根据式(2) 求m′的校验码为m′G,根据m′G和p′可以求出症候s.如
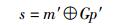
|
(4) |
若未发生数据位翻转,则m′G应与p′完全相同,即症候s等于0.若症候s不为0,表明码字中发生了错误.得到症候码s后,采用式(5) 的校验矩阵H来做译码纠错:

|
(5) |
在H矩阵里,前面8列是原码m的症候向量s,后面8列是症候向量所对应的错误向量e,根据e可以得到具体的错误位,从而实现1位纠错. 2位错误的症候是矩阵中每两列症候的和,对应的错误向量同样求和,可得出2位错误的位置,实现2位纠错.同理,可以得到3位错误的症候向量.但3位错误症候有重码,所以3位只能检验,而不能实现纠错.
通过构建查找表,分别求出原码和校验码错误后的错误向量em、ep,再利用em、ep和接收原码m′以及校验码p′,求出纠错后的正确向量m*、p*,完成译码纠错过程,如
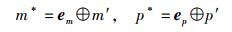
|
(6) |
(16, 8) 准循环码的编译码方式适合用FPGA实现,8位的编译码结构也适合FPGA内部的RAM构造.利用内置RAM做容错FSM设计时,将FSM的基本状态和输入设定为RAM的存储地址,结果输出和状态转移作为存储内容.为了保证输入状态也可以被编码检错,将输入、输出和转移态同时编码存储在RAM内.下面以简单的5状态的FSM为例,详述利用(16, 8) 准循环码设计容错FSM的原理和主要思路.
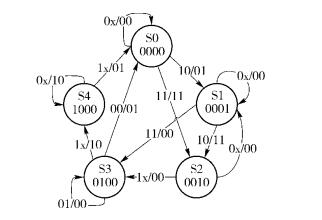
2.2.1 FSM编码定义假定5状态FSM结构如图 1所示.双端口RAM定义及FSM映射说明如表 1所示,FSM映射数据已经按照指定算法计算并存储至RAM中.
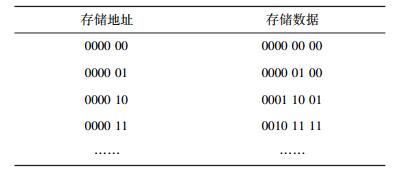
从表 1中可以看出, 当RAM地址为0000 00时,其存储内容为0000 00 00;当输入变为01时,RAM地址变为0000 01,此时RAM内数据为0000 01 00;如果此时输入11时,RAM地址变为0000 11,则RAM内数据变为0010 11 11.以此类推,输入值的变化,可以改变RAM的地址,通过地址取出的RAM内数据即为FSM的转移态和输出值,从而实现FSM的正常工作.
|
|
表 1 双端口RAM地址数据定义说明 |
|
图 1 5状态FSM示例(0x表示00或01状态) |
RAM内数据m(即原始码)确定后,直接对m按式(2) 进行编码,即得到m的校验码p.原始码m与编码p用同一时钟采样存储在2个双端口RAM中,共用一个写存储地址.
初始化RAM读地址,使FSM处于初始状态.以RAM内数据高4位为地址高4位,输入状态做RAM地址低2位.当输入状态改变时,RAM地址跳变,输出当前存储值m′和p′.按照式(4) 计算症候和差错向量,如有1或2位翻转,利用症候查找表反算求出正确的m*和p*,再写回RAM内,完成实时纠错.同时设置错误显示标识error_flag,00:无错误翻转,01:1位错误翻转,10:2位错误翻转,11:3位错误翻转. 3位错误翻转可以被检测,但不能纠正.
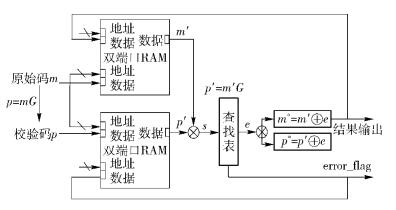
基于RAM的(16, 8) 码FSM物理实现原理框图见图 2.
|
图 2 (16, 8) 码容错FSM原理图 |
根据上述分析,利用Xilinx Virtex-Ⅱ FPGA器件XC2V3000搭建模拟测试平台,并在该模拟平台上运行基于(16, 8) 码的FPGA容错FSM程序.
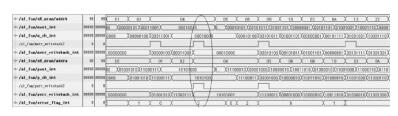
模拟空间辐射造成的错误激励由FPGA内部测试模块产生,呈循环随机插入状态,错误位置包括源码m和纠错码p,测试主时钟80MHz.测试时采用Xilinx内置逻辑分析仪工具实时捕捉错误插入和纠错后波形.源码为m_int,纠错码为p_int采用组合逻辑实现,与源码同步生成,无系统延时.插入错误后源码发生翻转,同时纠错码相应变化.翻转后错误码写入RAM中模拟数据被打翻,错误插入示例如图 3所示.对RAM内读出的错误数据进行检错和纠错,可看到纠错后数据m_ch_int和p_ch_int回到了正确状态,同时error_flag给出错误位数标识,如图 4所示.延时后的纠错数据merr_writeback_int2、perr_writeback_int2反写回各自的RAM中. RAM内数据在3个时钟周期里完成译码、纠错和数据刷新,因此系统在延时3个时钟后可被重新配置,实时性能良好. FSM后续运转时不再出现错误翻转,二位错误翻转被纠正,FSM的跳转及输出均正常,如图 5所示.对于3位错误翻转,系统给出error_flag标志“11”.

|
图 3 错误激励输入 |

|
图 4 纠错后FSM运行效果 |
|
图 5 出错状态纠正 |
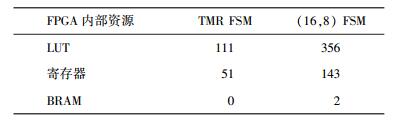
(16, 8) 编译码规则易于实现,但解码查找表略大,(16,8) FSM和普通FSM用TMR的资源占用率对比如表 2所示.
在系统延时上,(16, 8) FSM在正常启动后的运行状态间延时与TMR FSM相同,但由于启动前要译码纠错,在初始激励输入后,会有最少3个时钟周期的延时,较TMR FSM系统延时偏长.
|
|
表 2 TMR FSM与编码FSM资源占用比对 |
双端口RAM存储器基本单元的可靠性如式(7) 所示, 服从泊松分布[6].
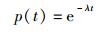
|
(7) |
对于一个输入位宽为n、输出位宽为m和状态编码位宽为s的FSM, 存储单元在时间t内不发生SEU的概率为
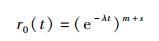
|
(8) |
未加容错设计保护的FSM的一个存储单元的可靠性为r0-one(t)=r0(t).
在时间t内仅有1处SEU发生的概率为
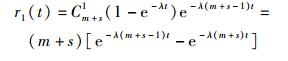
|
(9) |
采用1位纠错设计(如汉明码)保护的FSM,其一个存储单元的可靠性为
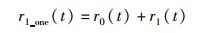
|
(10) |
在时间t内仅有2处SEU发生的概率为
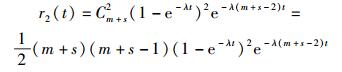
|
(11) |
基于RAM的FSM有(16,8) 准循环码保护的FSM,其一个存储单元的可靠性为
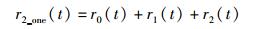
|
(12) |
用于构建FSM的RAM有2n+s个存储单元,所以基于RAM全部存储单元的FSM在时间t内的可靠性为
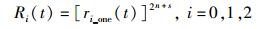
|
(13) |
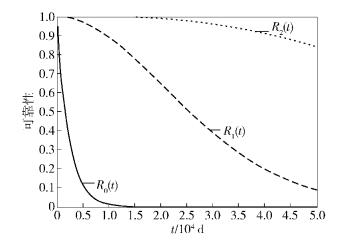
NASA提供了实验用粒子束条件下,FPGA块RAM的翻转率为λ=1.1×10-6位/d,以图 1中的FSM为例,即m=2,s=4,n=2.经过分析计算,R0、R1和R2的可靠度计算结果如图 6所示.采用(16, 8) 准循环码容错设计保护的FSM的可靠性要高于采用汉明码或没有容错设计保护的FSM.
|
图 6 FSM可靠度对比 |
(16, 8) 准循环码容错FSM针对星载平台FSM的稳定性问题,是一种可以有效检验和纠正FPGA内FSM 2位错误翻转的高可靠容错设计方法,具有以下突出特点:1) 实时纠正1位或2位翻转错误,可检测3位翻转错误,提高了FSM的容错能力;2) 系统延时小,满足实时控制系统的需要;3) 相关设计硬件易实现,当状态机编码超过8位时,采用两片RAM并行即可扩容到16位状态.综合来看,基于(16, 8) 编码的容错FSM系统延时小,硬件实现方便,可以应用于对可靠性有较高要求的小卫星控制系统、星上实时信号处理系统以及其他辐照环境下电子系统的设计,是一种有发展潜力的高可靠容错FSM的设计方案.
| [1] | Lusala A K, Legat J. A hybrid NoC combining SDM-TDM based circuit-switching with packet-switching for real-time applications[C]//2012 IEEE 10th International New Circuits and Systems Conference. Montreal, QC, Canada: IEEE Press, 2012: 17-20. |
| [2] | Chang Linhuang, Lee T H, Chu Hungchi, et al. QoS-aware path switching for VoIP traffic using SCTP[J]. Computer Standards & Interfaces, 2013, 35(1): 158–169. |
| [3] | Blake S, Black D, Carlson M, et al. RFC 2475—1998, an architecture for differentiated services [S]. New York: IETF, 1998: 12-25. |
| [4] | Clos C. A study of nonblocking switching networks[J]. Bell System Technical Journal, 1953, 32(2): 406–424. doi: 10.1002/bltj.1953.32.issue-2 |
| [5] | Eiji O, Jing Zhigang, Roberto R C, et al. Concurrent round-robin-based dispatching schemes for Clos-network switches[J]. IEEE/ACM Transactions on Networking, 2002, 10(6): 830–844. doi: 10.1109/TNET.2002.804823 |
| [6] | Liew S Y, Lee T T. Bandwidth assignment with QoS guarantee in a class of scalable ATM switches[J]. IEEE Transactions on Communications, 2000, 48(3): 377–380. doi: 10.1109/26.837040 |
| [7] | Li Xin, Zhou Zhen, Hamdi M. Space-memory-memory architecture for Clos-network packet switches[C]//2005 International Conference on Communications. Seoul, South Korea: IEEE Press, 2005: 1031-1035. |