2. 武警北京指挥学院, 北京 100012;
3. 国瑞数码安全系统有限公司, 北京 100088
提出了一种利用二维熵分量的K均值攻击效果聚类评估方法.利用网络熵预处理攻击数据集,将效果数据映射到二维平面,并以二维熵分量作为聚类的输入,然后基于K均值算法建立聚类数据集与效果分类之间的关系,实现了对网络攻击效果结果集的明确划分,并提供快速有效的评估结果.仿真实验结果证明,该方法能高效正确地处理攻击数据,并以评估结果类图的形式提供直观的评估结果.
2. Armed Police Beijing Command Academy, Beijing 100012, China;
3. National Cybernet Security Ltd, Beijing 100088, China
A K-means cluster evaluation technique using bi-dimensional entropy components was proposed. The attack dataset on the basis of network entropy was preprocessed, a two-dimensional plane was mapped. The output of preprocess as the input of clustering was utilized. And a relation between the attack dataset and the effect category on the basis of K-means algorithm was established, thus an explicit division of attack effect set was achieved. Efficient evaluation was given. Experiment shows that the method can process attack dataset with high efficiency, as well as provide a visualized evaluation result by form of evaluation cluster diagram.
网络攻击行为正朝着目标各异、手段多变、攻击方式组合化的方向发展,这给网络安全防御工作带来了很大的挑战.其中,作为检验攻击的有效性和网络安全性的重要手段,网络攻击效果评估技术也面临着新的技术局限性.目前针对攻击效果评估的研究集中在效果分级和指标权值上,付钰、张琳等[1-2]从评估标准模糊性、权重分配等角度对网络攻击效果评估进行了研究,另一方面,聚类分析作为数据挖掘中的重要手段,在网络安全分析方面也得到了探索性的应用,包括基于聚类分析的入侵检测、僵尸网络检测、脆弱性检测等[3-4].
基于K均值聚类的攻击效果评估方法,能简化评估数据预处理步骤,直观动态地反映出攻击对系统造成的影响,在满足批量运算效率要求的同时克服评估过程的主观性.
1 基于熵差的攻击效果评估信息论之父C.E.Shannon提出了信息熵的概念,并用离散随机事件发生概率给出了其计算公式:

|
(1) |
其中:pi∈(0, 1]表示随机事件发生概率,k>0为常数.由定义,随机事件发生的概率越小,则熵值越大,其不确定性越大.受信息熵的启发,在研究攻击效果评估方法中可以引入相应的网络熵[5]的概念,以目标网络受攻击前后的指标值Va、Vb为参数,对每个归一化指标值Vi,攻击发生前后的熵差为
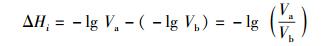
|
(2) |
可知,网络遭受攻击之后,熵差ΔHi随着指标差值Va/Vb的增大而增大,即攻击效果越明显,能直观地表征网络在攻击前后性能的变化.
2 基于二维熵的K均值聚类评估K均值聚类方法应用到网络攻击效果评估中,能针对攻击数据集多样性和同一性一体的特点,利用K均值算法将熵差聚类,对量化的攻击效果做定性的评估.首先对攻击数据预处理,计算攻击前后的熵差并映射到二维向量空间,在反映数据特点的同时统一标度,然后利用改进K均值算法聚类,以网络攻击效果的分级特性作为启发式信息确定聚类数,针对评估数据分级特性,假定初始聚类中心等距分布,计算二维向量空间中各数据点的欧几里得中心为初始聚类中心,以减少迭代次数、降低异常点对聚类效果的影响.经过数轮迭代后,最终选取使距离代价函数最小的聚类结果作为最终输出以评估攻击效果.
2.1 数据预处理数据预处理是数据规范化的过程,通过对攻击数据的变换、规约操作提高评估核心操作的效率和质量.
对给定攻击时间内的指标组V={V1, V2, …, Vi, …},攻击前后Vi的指标熵分别为Hi和Hi′,尽管熵差大小可以反映受攻击前后的变化,但是不同指标的度量方式不一样,熵差本身的值差别可能很大,仅从数据大小上无法反映攻击效果,因此,对每个指标引入最大可能攻击效果熵Hmax对指标值规格化,根据实际熵差和理想熵差的比值来确定攻击的程度.定义攻击效率变量θi,将每组数据描述为Ai=(Hi, H′i, Hmax, θi),其中Hi、H′i、Hmax分别表示攻击前后性能熵以及指标理想最大熵,以熵差公式计算. θi为攻击效率变量:假设第i组数据对应的攻击时间为Ti,Ti表示达到攻击效果需要花费的时间,则攻击效率变量θi的余弦值为cos θi=Ti,为计算方便,采用最小—最大规范化方法对Ti进行线性变换,将其映射到[0, π/2].此时,进行规范化的原始数据值域为[0, α](α为效果评估实施时给定的攻击时间段),规范化输入数据即Ti∈[0, α],Ti的取值严格落于原始数据值域之间,在最小—最大规范化过程中不会出现“越界错误”,同时,能保持原有数据间联系.最小—最大规范化公式为
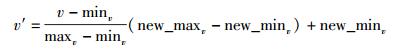
|
(3) |
其中:v′为规范化后数据,v为原始数据,maxv和minv为原始数据上下界,new_maxv和new_minv为规范化后数据上下界,对于攻击时间,显然其下界为零,上界为α.得攻击效率变量: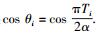
可以看到,在其定义域上,cos θi是单调减函数,Ti越小表示攻击效率越高,在Ti相等的情况下,实际攻击效果量高低由熵差的数值大小决定.通过以上的处理,引进攻击效率变量θi可以将各攻击数据点的单一数据值映射到二维向量空间,对Ai=(Hi, H′i, Hmax, θi),以熵差的大小表示向量的长度,与x轴的夹角θi确定向量的方向,根据余弦定理,经映射变换后的数据点Ai可表示为
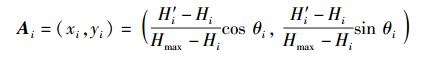
|
(4) |
对指标数据预处理之后,利用K均值算法的原理对数据点聚类以评估攻击效果,步骤如下.
第1步 确定初始评估中心.首先选取聚类数,可参照通用漏洞评分系统(CVSS,common vulnerability scoring system)将初始攻击效果集选取为Result={优,良,中,差},取聚类数初始值k0=4.根据数据点Ai的熵差和夹角(ΔHk, θk)计算点在直角坐标系下的坐标(xi, yi),根据对初始评估中心等距分布的假设,计算其坐标为
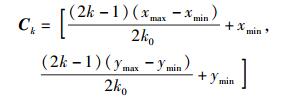
|
(5) |
第2步 划分数据点所属评估结果集.分别求出每个数据点到评估中心Ck的欧氏距离,存储到矩阵D0中,并将节点划分到有最小距离的结果集.计算紧致与分离性效果函数S(U, k)作为距离代价函数,
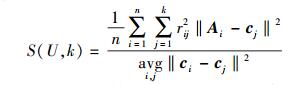
|
(6) |
其中:n为数据点总数,k为结果集数,Ai代表第i个数据点,cj代表第j个评估中心,‖Ai-cj‖2为数据点Ai与评估中心cj 2-范数的平方,在二维向量空间中表示Ai与cj的向量距离,rij为Ai对cj的隶属度且
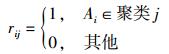
|
(7) |
可以看到,紧致与分离性效果函数衡量了类内距离与类间距离的比值,类内距离越小,类间距离越大,则效果函数值越小,表示聚类效果越好.
第3步 重算评估中心.聚类过程中需要保证类间距离尽可能小,假定新评估中心为μk,则数据点Ai到新评估中心的均方差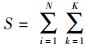
对参数rik,显然将其划分到距离最近的评估中心所属聚类时可以保证S最小,即
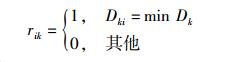
|
(8) |
对μk求导,有
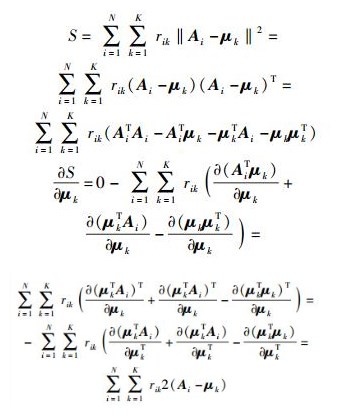
|
令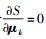
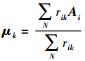
第4步 优化聚类结果.一次聚类过程结束后,得到评估结果Cluster0,再优化聚类数k.由于初始时k以经验确定,可能存在细微偏差,计算新聚类数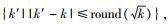
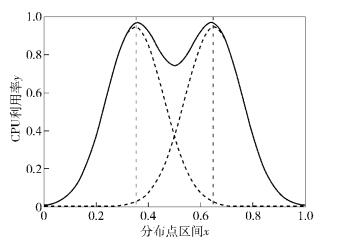
实验时,利用Matlab进行仿真,以针对资源消耗型攻击的效果评估为例,产生符合如图 1的联合高斯分布X~N(0.35, 0.1)+N(0.65, 0.1) 数据点作为主机攻击后的中央处理器(CPU,central processing unit)利用率.
|
图 1 输入数据点联合高斯分布 |
假设对30台主机每台发起30次攻击试验,产生900个(0, 1) 间如图 1高斯分布的数据点,联合高斯分布图中大部分数据分布在(0, 0.4) 之间,因此,可预测最终评估结果中攻击效果为{中,差}的将占大多数.为了验证这一预测,将初始聚类数设为4,优化时对聚类数k~{2, 3, 4, 5, 6}迭代,求得紧致与分离性函数值Sk={35.69, 22.18, 12.25, 14.79, 20.12} (k = 2, …, 6),当k=4时Sk最小,取聚类数k=4为最优输出结果,如图 2所示.
|
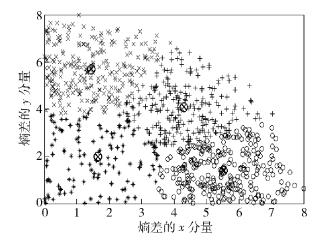
图 2 聚类结果(k=4) |
由聚类结果知,算法将900个数据点的输入按攻击效果好坏程度分为4类,可结合实际给出这4类攻击的定性描述{优,良,中,差},其中较少数攻击产生“好”的效果,如图 2中远离y轴的“○”点所示,越靠近y轴数据点攻击效果越差.
对以上结果进行统计,聚类结果为{优,良,中,差}的数据点数分别为{271, 241, 129, 259}个,可利用此数据分布对结果进行统计分析.例如,若将攻击效果为“优”和“良”的数据作为有效攻击数据,将攻击效果为“中”的数据作为部分有效攻击数据,可计算攻击效率为64.06%.由图 2的聚类结果也可以直观地看到对攻击效果的阶梯式的分类.
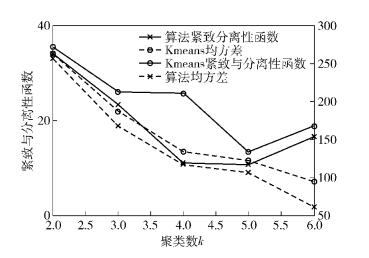
为了验证本算法初始聚类中心的合理性以及聚类的质量以支持聚类评估的可行性,将算法与传统K均值算法作聚类性能的比较,分别比较其均方差及紧致与分离性函数,比较结果如图 3所示,可以看到,在聚类数分别为2~6的情况下,就算法本身而言,其紧致与分离性距离代价函数和节点距离均方差均在聚类数k=4时达到最优,且均优于K均值聚类结果的相应值,说明本算法的聚类结果是可信的,可以有效表示攻击效果的不同级别.
|
图 3 聚类评估算法性能验证 |
此外,为了验证算法对攻击数据处理的有效性,利用国际知识发现和数据挖掘竞赛(KDDCUP,knowledge discovery and data mining)99入侵检测数据集中的采样数据进行仿真实验.数据集包含500万条记录,其中每个数据项包括41个特征描述,涵盖了包括传输控制协议(TCP,transmission control protocol)连接基本特征到网络流量统计特征在内的相关信息,本次实验对teardrop标签下的979条数据项进行抽样,提取600个攻击数据点,将duration特征作为攻击持续时间Tk以计算攻击效率变量,分别针对攻击前后的count(与当前连接具有相同目标主机的连接数)、srv_count(与当前连接具有相同服务的连接数)以及hot(访问系统敏感文件目录次数)特征值计算熵差进行聚类评估,仿真结果如图 4所示.
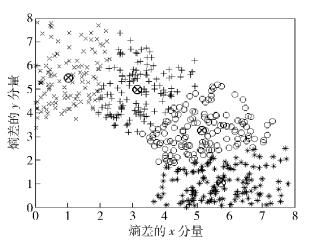
|
图 4 KDDCUP攻击数据集评估结果 |
根据聚类结果,结合KDDCUP数据集中的数值,可以得到表 1所示的攻击效果分级描述.
|
|
表 1 KDDCUP攻击数据集效果分级 |
通过借鉴网络熵的思想,引入理想最大熵以归一化不同数据类型的熵差,并考虑达到理想攻击效果的时间引入攻击效率分量,能将数据点通过余弦定理映射到二维向量空间,然后利用预设聚类中心的K均值聚类算法进行攻击效果分级计算.仿真实验证明该算法既保持了传统K均值算法快速收敛的特性,又通过聚类中心的处理克服了K均值算法容易陷入局部最优解的问题,能有效处理攻击数据并呈现可视化的效果分类结果.然而,算法还有待完善的地方.例如,在计算多种不同攻击对目标网络造成的效果时,除了攻击程度外,还需考虑攻击危害性赋权问题以界定攻击对网络更高层次的属性带来的影响,此外,还有定性指标值的量化问题,这些都是值得进一步研究的课题.
| [1] |
付钰, 吴晓平, 叶清, 等. 基于模糊集与熵权理论的信息系统安全风险评估研究[J]. 电子学报, 2010, 38(7): 1489–1494.
Fu Yu, Wu Xiaoping, Ye Qing, et al. An approach for information systems security risk assessment on fuzzy set and entropy-weight[J]. Acta Electronica Sinica, 2010, 38(7): 1489–1494. |
| [2] |
张琳, 刘婧文, 王汝传, 等. 基于改进D-S证据理论的信任评估模型[J]. 通信学报, 2013, 34(7): 167–173.
Zhang Lin, Liu Jingwen, Wang Ruchuan, et al. Trust evaluation model based on improved D-S evidence theory[J]. Journal on Communications, 2013, 34(7): 167–173. |
| [3] | Wazid, Katal, Goudar. Cluster and super cluster based intrusion detection and prevention techniques for jellyfish recorder attack[C]//PDGC 2nd IEEE International Conference. 2012: 435-440. |
| [4] | Partha Sarathi Bishnu, Vandana Bhattacherjee. Software fault prediction using quad tree-based K-means clustering algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(6): 1146–1150. doi: 10.1109/TKDE.2011.163 |
| [5] |
张义荣, 鲜明, 王国玉. 一种基于网络熵的计算机网络攻击效果定量评估方法[J]. 通信学报, 2004, 25(11): 158–165.
Zhang Yirong, Xian Ming, Wang Guoyu. A quantitative evaluation technique of attack effect of computer network based on network entropy[J]. Journal of China Institute of Communications, 2004, 25(11): 158–165. doi: 10.3321/j.issn:1000-436X.2004.11.022 |



