2. 网络体系构建与融合北京市重点实验室, 北京 100876;
3. 无线移动通信国家重点实验室 电信科学技术研究院, 北京 101149
提出了一种用于下行协作多点系统联合传输的和空间干扰对齐(IA)机制.利用多小区联合预编码将从不同基站到同一用户的干扰对齐到一个特定维度的空间中,实现干扰空间的压缩;然后在接收端设计干扰抑制矩阵消除多用户间干扰.从系统自由度(DoF)的角度理论分析了和空间IA机制的性能,给出了系统可达DoF上界,以及干扰信号压缩维度与系统可达DoF的关系.数值仿真将和空间IA机制与传统正交机制和经典IA机制进行对比,验证了和空间IA机制可以获得更高的DoF与数据速率.
2. Beijing Key Laboratory of Network System Architecture and Convergence, Beijing 100876, China;
3. State Key Laboratory of Wireless Mobile Communications, China Academy of Telecommunication Technology, Beijing 101149, China
A sum-space interference alignment (IA) scheme for downlink coordinated multi-point joint transmission system was proposed. The interference from the collaborative base stations to each user equipment was aligned onto a space of specific dimension, which was accomplished by joint precoding for multiple coordinated cells, and then the interference space was compressed. The interference can be eliminated by interference suppression matrix which was designed at the each user equipment side. In the performance analysis, the outer bound of the system total achievable degree of freedom (DoF) was derived, and the relationship between the achievable DoF and the dimensions of the aligned interference space was given. Numerical analysis shows that the sum-space IA scheme can obtain more DoF and data rate compared with traditional orthogonal schemes and traditional IA schemes.
协作多点(CoMP, coordinated multi-point)技术可以有效抑制小区间干扰,但协作区域内多用户间干扰会影响系统的频谱效率.干扰对齐(IA, interference alignment)技术在发送端进行预处理,利用一定的自由度(DoF, degree of freedom)将干扰限制在特定空间内,同时在接收端通过迫零处理消除干扰[1].
Changho等[2]提出了适用于蜂窝网络的子空间IA机制来增加有用信号的维度.卢华兵等[3]针对两小区蜂窝网络的边缘用户提出一种低开销IA机制,利用预编码矢量消除小区内用户间干扰,利用干扰抑制矢量消除小区间干扰.章扬等[4]提出的基于严格势博弈的分布式IA机制也可用于蜂窝网络,通过最大化净效用函数求出预编码矩阵和干扰抑制矩阵. Shin等[5]和Ma Yanjun等[6]通过用户协作设计的IA机制可以获得较高的系统DoF.
上述研究的场景都等效于CoMP中的协作调度/协作波束成型系统,笔者提出了一种适用于联合传输(JT, joint transmission)系统的和空间IA机制并分析了其性能.在基站端进行联合预编码,将干扰对齐到一个d维空间,进而减小干扰空间的维度;设计用户端干扰抑制矩阵,使其处于d维空间的零空间,进而消除用户间干扰,解调有用信号.
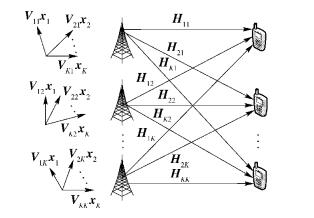
1 CoMP系统JT模型多小区协作JT系统模型如图 1所示. K(K≥2) 个基站协作为K个用户进行服务,每个基站的发送天线数为NT,每个用户的接收天线数为NR.
|
图 1 K小区协作JT示意图 |
基站j的发送信号为
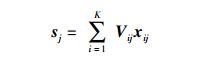
|
(1) |
其中:xij为从基站j发送到用户i的信号矢量,Vij为基站j传输xij的预编码矩阵.在CoMP-JT系统中,所有基站到用户i的信号相同,后文把xij简写为xi,表示发送到用户i的信号矢量.每个基站的发送信号需要满足一个平均功率限制,即
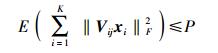
|
其中P为平均发送功率.定义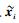
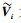
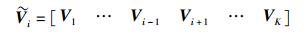
|
(2) |
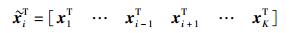
|
(3) |
其中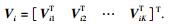
用户i的接收信号为
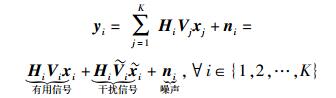
|
(4) |
式(4) 等号右边第1项表示用户i接收的有用信号,第2项表示用户i接收的干扰信号,ni~CN(0, σ2I)表示零均值加性高斯白噪声.从基站到用户i的信道矩阵为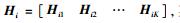
每个用户通过乘以一个干扰抑制矩阵来解调有用信号,用户i接收机处理之后的信号为
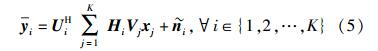
|
(5) |
其中:UiH为干扰抑制矩阵,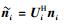
和空间IA机制的主要思想:首先,通过设计预编码矩阵,加和从所有基站到同一个干扰用户的有效信道矩阵;然后,把所有加和后的有效信道矩阵的列空间对齐到同一d维空间,进而降低干扰空间维度,使系统预留更多空间传输有用信号;最后,设计干扰抑制矩阵,使其处于d维干扰空间的零空间,进而去除干扰.预编码矩阵和干扰抑制矩阵需要满足的IA条件为

|
(6) |
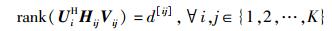
|
(7) |
式(6) 保证了所有的干扰为零,式(7) 保证了矩阵UiHHijVij满秩,意味着用户i可以从基站j到用户i这条链路上获得的DoF为d[ij],则用户i的DoF为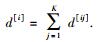
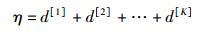
|
(8) |
定义 一个用户的和空间为所有基站到这个用户的和有效信道矩阵的列空间.对于用户i(∀i∈{1, 2, …, K}),有用信号的和空间为
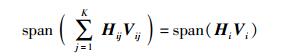
|
其中span(A)表示矩阵A的列空间.目的为用户k的干扰信号的和空间为
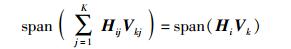
|
为了将K-1个干扰信号的和空间全部对齐到一个d维空间,预编码矩阵需要满足的条件为
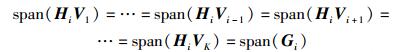
|
(9) |
其中Gi∈CNR×d(∀i={1, 2, …K})的列向量表示对齐后干扰空间的一组正交基.可以简单地把矩阵Gi的列向量设置成单位矩阵INR的d个特征向量.于是,预编码矩阵应该满足

|
(10) |
其中Ci, k(∀i, k∈{1, 2, …, K}, k≠i)为将干扰空间的基从HiVk的列向量改变为Gi的列向量的过渡矩阵.根据过渡矩阵的性质,可以把Ci, k设计为任意d维非奇异矩阵.式(10) 简化为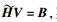
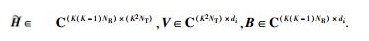
因为信道是块衰落信道,所以式(10) 可以保证Pr {span(HiVi)=span(Gi)}=0(∀i={1, 2, …, K}).为了解码出有用信号,必须保证span(Gi)的正交补空间span(Gi⊥)存在,即必须满足d < NR.式(10) 不能为超定方程,即天线数应该满足条件KNT≥(K-1)NR.因为信道是块衰落信道,所以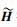
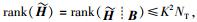
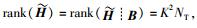
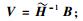
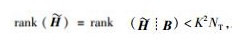
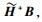
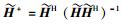
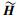
联合预编码后,用户i的接收信号可以表示为
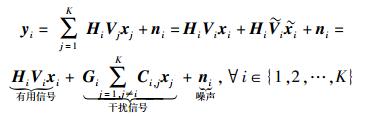
|
(11) |
为了消除多用户间的干扰,用于用户i的干扰抑制矩阵应该满足UiHGi=0,即
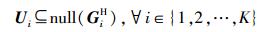
|
(12) |
其中null(A)表示矩阵A的零空间.
干扰抑制矩阵的设计思路:① 消除多用户间干扰,使多用户多输入多输出(MIMO, multiple-input multiple-output)信道等效为多个并行的、用户间无干扰的单用户MIMO信道;② 消除数据流之间的干扰,使系统的容量最大化.具体过程如下.
对GiH进行奇异值分解:
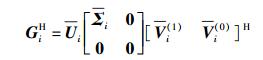
|
(13) |
其中:Σi为对角矩阵,其元素为GiH的非零奇异值,维度等于GiH的秩;Vi(1)由GiH的d个非零奇异值对应的特征向量组成;Vi(0)由GiH的NR-d个零奇异值对应的特征向量组成.因此,GiHVi(0)=0,于是矩阵diag(V1(0)HH1V1, V2(0)HH2V2, …, VK(0)HHKVK)为块对角矩阵,意味着多用户间干扰已经被消除.
对(HiVi)HVi(0)进行奇异值分解:
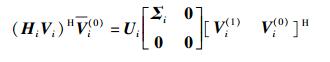
|
(14) |
其中Vi(1)由(HiVi)HVi(0)的非零奇异值对应的特征向量组成,可以进一步消除数据流间的干扰,使矩阵
令Ui=Vi(0)Vi(1),干扰抑制矩阵为
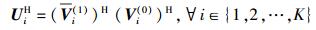
|
(15) |
通过上面设计的干扰抑制矩阵,用户可以解调有用信号,则用户i的接收信号为
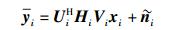
|
(16) |
定理1 在K(K≥2) 小区下行CoMP-JT系统中,K个基站为K个用户进行服务,每个基站的发送天线数为NT,每个用户的接收天线数为NR,并且KNT≥(K-1)NR.如果系统采用和空间IA机制:① 每个用户的干扰将被压缩到d维空间中;② 系统的可达DoF上界为min(K2NR/(K+1), KNT).
证明 在第i个用户端,干扰空间为span(Hi1Vj1, Hi2Vj2, …, HiKVjK)(∀i, j∈{1, …, K}, j≠i).如果采用和空间IA机制,干扰空间为span{Gi},其维度最大为d,能解调的有用信号空间为span(Gi⊥),分以下2种情况进行讨论.
1) 如果Kd≤NR-d,则dim {span(Gi⊥)}=Kd,用户i可以获得的最优DoF为Kd,即d[i]=Kd,意味着每个用户可以解码Kd维独立数据流,因此,系统可以传输K2d维独立数据流,即系统可达DoF为η=K2d.因为每个基站发送的独立数据流数应小于等于发送天线数,即Kd≤NT,所以系统的可达DoF上界为min (K2NR/(K+1), KNT).
2) 如果Kd>NR-d,则dim {span(Gi⊥)}=NR-d,用户i可以获得的最优DoF为NR-d,即d[i]=NR-d,意味着每个用户可以解码NR-d维独立数据流,因此,系统可以传输K(NR-d)维独立数据流,即系统可达DoF为η=K(NR-d).因为NT≥Kd>NR-d,所以系统可达DoF上界为min(K2NR/(K+1), KNT).若d=NR/2,则η=KNR/2,与传统IA机制[1]的可达DoF相同.
综上所述,当每个用户的干扰被压缩到d维空间时,系统可达DoF上界为min(K2NR/(K+1), KNT),当d=min (NR/(K+1), NT/K)时,DoF达到上界.
3 数值仿真为了评估和空间IA机制的性能,分别对其可达DoF和可达速率进行仿真.仿真场景为3个基站协作为3个用户服务,每个基站的发送天线数为NT,每个用户的接收天线数为NR.仿真使用高斯干扰信道,信道矩阵元素独立同分布且都服从均值为0、方差为1的复高斯分布.
由定理1可知,和空间IA机制的适用条件为NT≥(K-1)NR/K,可以分为以下2种情况.
情况1 NT≥KNR/(K+1).此时系统DoF主要取决于接收天线数,仿真选取满足条件的最小发送天线数,即NT=「KNR/(K+1)⌉.
情况2 (K-1)NR/K≤NT≤KNR/(K+1).此时系统DoF主要取决于发送天线数,仿真选取满足条件的最小接收天线数,即NR=「(K+1)NT/K⌉.
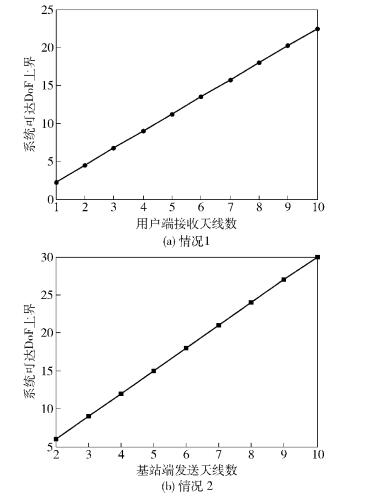
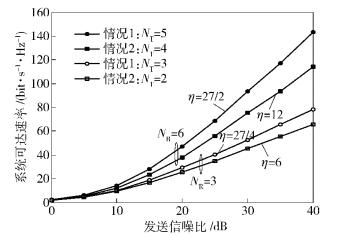
图 2给出了和空间IA机制的系统可达DoF上界,图 3给出了NR=3和NR=6时的系统可达速率.由图 2可以看出,情况1的系统可达DoF上界会随着接收天线数的增加而线性增加;情况2的系统可达DoF上界会随着发送天线数的增加而线性增加.由图 3可以看出,当接收天线数一定时,发送天线数越大,系统的可达速率越大.
|
图 2 系统可达DoF |
|
图 3 系统可达速率 |
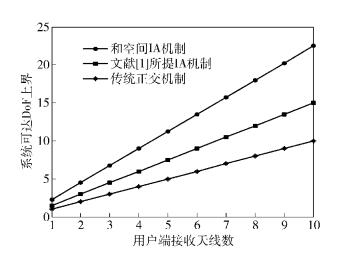
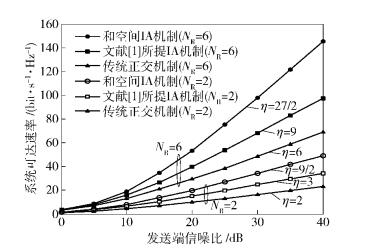
当NT=NR时,将和空间IA机制与传统正交机制、经典IA机制[1]进行对比. 图 4比较了3种机制的系统可达DoF上界,图 5比较了NR=2和NR=6时3种机制的系统可达速率.由图 4可知,和空间IA机制的可达DoF较其他2种机制都有明显提升.另外,曲线也显示了当天线数越大时,系统的可达DoF越大,利用JT技术的增益也越明显.由图 5可以看出,当接收天线数相同时,和空间IA机制的可达速率较其他2种机制都有一定提升,并且同一种机制的可达速率会随着接收天线数的增加而增加.
|
图 4 可达DoF的比较 |
|
图 5 可达速率的比较 |
笔者提出了一种用于下行CoMP-JT系统的和空间IA机制. 从数值分析中可以看出,这种机制可以把干扰压缩到较小维度的空间中,并且与传统正交机制和文献[1]提出的经典IA机制相比,可以得到更大的DoF. 下一步的工作主要是研究非理想信道状态信息对和空间IA机制性能的影响.
| [1] | Cadambe V R, Jafar S A, et al. Interference alignment and degrees of freedom of the K-user interference channel[J]. IEEE Transactions Information Theory, 2008, 54(8): 3425–3441. doi: 10.1109/TIT.2008.926344 |
| [2] | Changho S, Tse D. Interference alignment for cellular networks[C]//46th Annual Allerton Conference on Communication, Control, and Computing. Illinois:[s.n.], 2008: 1037-1044. |
| [3] |
卢华兵, 谢显中, 马彬, 等. 多天线两小区蜂窝系统的低开销线性干扰对齐算法[J]. 信号处理, 2012, 28(8): 1148–1155.
Lu Huabing, Xie Xianzhong, Ma Bin, et al. Low overhead linear interference alignment algorithm for two-cell MIMO cellular systems[J]. Signal Processing, 2012, 28(8): 1148–1155. |
| [4] |
章扬, 周正, 石磊, 等. 基于严格势博弈的干扰对齐[J]. 北京邮电大学学报, 2013, 36(2): 50–54.
Zhang Yang, Zhou Zheng, Shi Lei, et al. Interference alignment based on exact potential game[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 50–54. |
| [5] | Shin W, Lee N, Lim J B, et al. On the design of interference alignment scheme for two-cell MIMO interfering broadcast channels[J]. IEEE Transactions Wireless Communication, 2011, 10(2): 437–442. doi: 10.1109/TWC.2011.120810.101097 |
| [6] | Ma Yanjun, Li Jiandong, Chen Rui. On the achievability of interference alignment for three-cell constant cellular interfering networks[J]. IEEE Communications Letters, 2012, 16(9): 1384–1387. doi: 10.1109/LCOMM.2012.073112.120437 |


